Bucket Sort, also known as Bin Sort, is a distributed sorting algorithm, which sort elements from an array by performing these steps:
- Distribute the elements into buckets or bins.
- Sort each bucket individually.
- Merge the buckets in order to produce a sorted array as the result.
See the algorithm in action here and here.
The performance for execution time is:
| Case | Performance |
|---|---|
| Worst | O(n^2) |
| Best | Omega(n + k) |
| Average | Theta(n + k) |
Where n = the number of elements and k is the number of buckets.
In the best case, the algorithm distributes the elements uniformily between buckets, a few elements are placed on each bucket and sorting the buckets is O(1). Rearranging the elements is one more run through the initial list.
In the worst case, the elements are sent all to the same bucket, making the process take O(n^2).
A pseudocode of the algorithm can be as follows:
function bucketSort(array, n) is
buckets ← new array of n empty lists
for i = 0 to (length(array)-1) do
insert array[i] into buckets[msbits(array[i], k)]
for i = 0 to n - 1 do
nextSort(buckets[i]);
return the concatenation of buckets[0], ...., buckets[n-1]
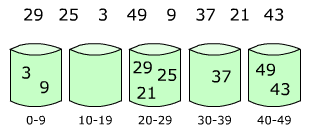
- Distribute elements in buckets:
- Sorting inside every bucket and merging:
Suppose we have the following list of elements: [2, 56, 4, 77, 26, 98, 55]. Let's use 10 buckets. To determine the capacity of each bucket we need to know the maximum element value, in this case 98.
So the buckets are:
bucket 1: from 0 to 9bucket 2: from 10 to 19bucket 3: from 20 to 29- and so on.
Now we need to choose a distribution function.
bucketNumber = (elementValue / totalNumberOfBuckets) + 1
Such that by applying that function we distribute all the elements in the buckets.
In our example it is like the following:
- Apply the distribution function to
2.bucketNumber = (2 / 10) + 1 = 1 - Apply the distribution function to
56.bucketNumber = (56 / 10) + 1 = 6 - Apply the distribution function to
4.bucketNumber = (4 / 10) + 1 = 1 - Apply the distribution function to
77.bucketNumber = (77 / 10) + 1 = 8 - Apply the distribution function to
26.bucketNumber = (26 / 10) + 1 = 3 - Apply the distribution function to
98.bucketNumber = (98 / 10) + 1 = 10 - Apply the distribution function to
55.bucketNumber = (55 / 10) + 1 = 6
Our buckets will be filled now:
1 :
[2, 4]
2 :
[]
3 :
[26]
4 :
[]
5 :
[]
6 :
[55, 56]
7 :
[]
8 :
[77]
9 :
[]
10 :
[98]
We can choose to insert the elements in every bucket in order, or sort every bucket after distributing all the elements.
Finally we go through all the buckets and put the elements back in the list:
[2, 4, 26, 55, 56, 77, 98]
Here is a diagram that shows the functions, data structures and protocols for our bucker sort implementation:
bucketSort() is a generic function that can apply the algorithm to any element of type T, as long as T is Sortable.
public func bucketSort<T:Sortable>(elements: [T],
distributor: Distributor,
sorter: Sorter,
buckets: [Bucket<T>]) -> [T] {
precondition(allPositiveNumbers(elements))
precondition(enoughSpaceInBuckets(buckets, elements: elements))
var bucketsCopy = buckets
for elem in elements {
distributor.distribute(elem, buckets: &bucketsCopy)
}
var results = [T]()
for bucket in bucketsCopy {
results += bucket.sort(sorter)
}
return results
}public struct Bucket<T:Sortable> {
var elements: [T]
let capacity: Int
public init(capacity: Int) {
self.capacity = capacity
elements = [T]()
}
public mutating func add(item: T) {
if (elements.count < capacity) {
elements.append(item)
}
}
public func sort(algorithm: Sorter) -> [T] {
return algorithm.sort(elements)
}
}public protocol Sortable: IntConvertible, Comparable {
}The algorithm is designed to sort integers, so all the elements to be sorted should be mapped to an integer value.
public protocol IntConvertible {
func toInt() -> Int
}public protocol Sorter {
func sort<T:Sortable>(items: [T]) -> [T]
}public protocol Distributor {
func distribute<T:Sortable>(element: T, inout buckets: [Bucket<T>])
}The current implementation make use of the following implementations for Sorter and Distributor.
Sorter
public struct InsertionSorter: Sorter {
public func sort<T:Sortable>(items: [T]) -> [T] {
var results = items
for i in 0 ..< results.count {
var j = i
while ( j > 0 && results[j-1] > results[j]) {
let auxiliar = results[j-1]
results[j-1] = results[j]
results[j] = auxiliar
j -= 1
}
}
return results
}
}Distributor
/*
* An example of a simple distribution function that send every elements to
* the bucket representing the range in which it fits.
*
* If the range of values to sort is 0..<49 i.e, there could be 5 buckets of capacity = 10
* So every element will be classified by the ranges:
*
* - 0 ..< 10
* - 10 ..< 20
* - 20 ..< 30
* - 30 ..< 40
* - 40 ..< 50
*
* By following the formula: element / capacity = #ofBucket
*/
public struct RangeDistributor: Distributor {
public func distribute<T:Sortable>(element: T, inout buckets: [Bucket<T>]) {
let value = element.toInt()
let bucketCapacity = buckets.first!.capacity
let bucketIndex = value / bucketCapacity
buckets[bucketIndex].add(element)
}
}By reusing this code and implementing your own Sorter and Distributor you can experiment with different versions.
The following are some of the variation to the general Bucket Sort implemented here:
Written for Swift Algorithm Club by Barbara Rodeker. Images from Wikipedia.