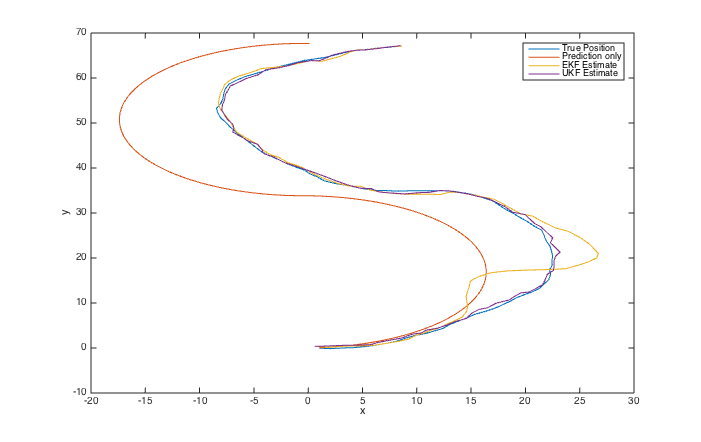
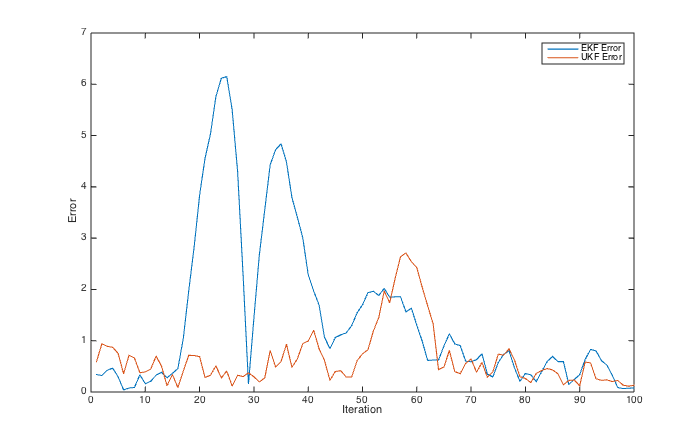
This example illustrates the use of the Kalman filter library for a simple planar 3DOF robot.
The robot state is given by a 3-vector containing the elements
- x: The x-position in the plane
- y: The y-position in the plane
- theta: The orientation (heading) relative to x-axis
The system model defining the evolution of the system state over time is fairly straight forward and is defined in SystemModel.hpp along with the control vector.
The system takes a velocity as well as a change in direction as control input. The robot then moves along the vector defined by the orientation plus the change in orientation.
Measurements of the system state are taken by two sensors: An orientation sensor (such as a compass) measuring the absolute heading as well as a position-sensor. However, the position cannot be measured directly, but only the euclidean distance to two landmarks (with known position) can be measured. This makes estimation of the true position quite challenging since the measurement and state are related by a highly non-linear equation.
The models and measurement vectors are defined in OrientationMeasurementModel.hpp and PositionMeasurementModel.hpp respectively.