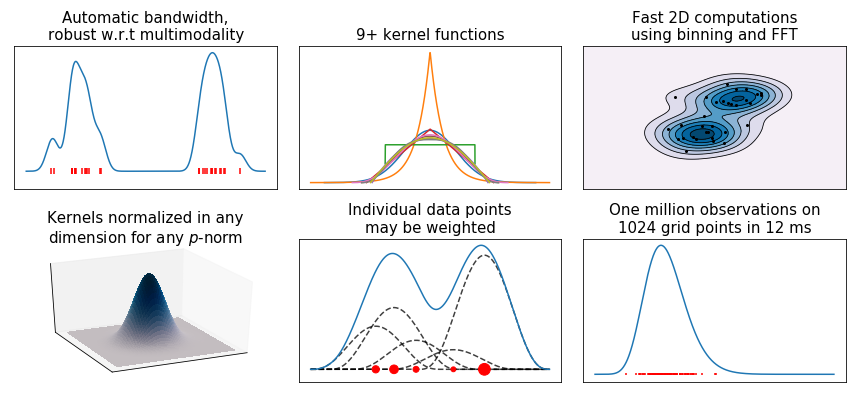
Want to cite KDEpy in your work? See the bottom right part of this website for citation information.
This Python 3.7+ package implements various kernel density estimators (KDE).
Three algorithms are implemented through the same API: NaiveKDE, TreeKDE and FFTKDE.
The class FFTKDE outperforms other popular implementations, see the comparison page.
The code is stable and in widespread by practitioners and in other packages.
The code generating the above graph is found in examples.py.
KDEpy is available through PyPI, and may be installed using pip:
pip install KDEpy
If you have trouble on Ubuntu, try running sudo apt install libpython3.X-dev, where 3.X is your Python version.
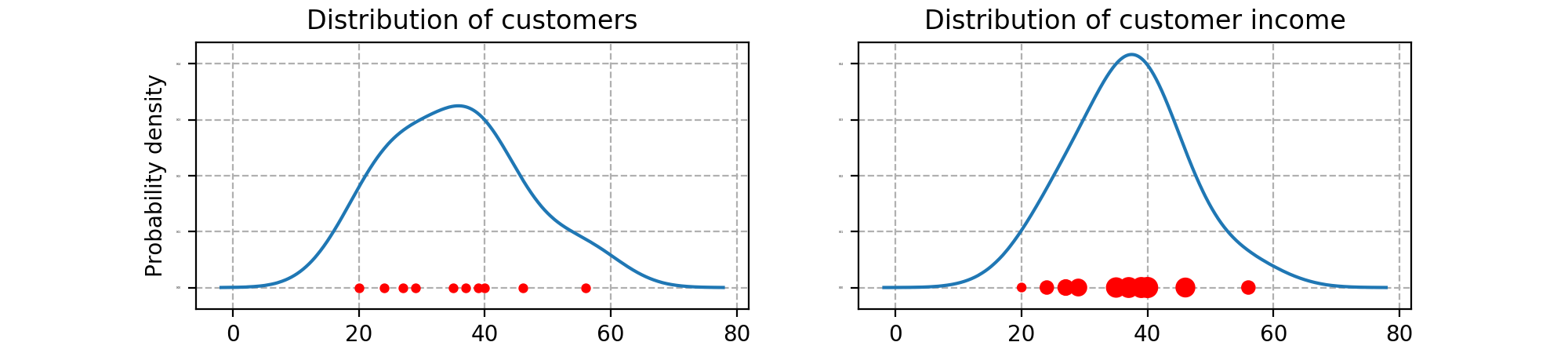
Below is an example showing an unweighted and weighted kernel density. From the code below, it should be clear how to set the kernel, bandwidth (variance of the kernel) and weights. See the documentation for more examples.
from KDEpy import FFTKDE
import matplotlib.pyplot as plt
customer_ages = [40, 56, 20, 35, 27, 24, 29, 37, 39, 46]
# Distribution of customers
x, y = FFTKDE(kernel="gaussian", bw="silverman").fit(customer_ages).evaluate()
plt.plot(x, y)
# Distribution of customer income (weight each customer by their income)
customer_income = [152, 64, 24, 140, 88, 64, 103, 148, 150, 132]
# The `bw` parameter can be manually set, e.g. `bw=5`
x, y = FFTKDE(bw="silverman").fit(customer_ages, weights=customer_income).evaluate()
plt.plot(x, y)The package consists of three algorithms. Here's a brief explanation:
NaiveKDE- A naive computation. Supports d-dimensional data, variable bandwidth, weighted data and many kernel functions. Very slow on large data sets.TreeKDE- A tree-based computation. Supports the same features as the naive algorithm, but is faster at the expense of small inaccuracy when using a kernel without finite support. Good for evaluation on non-uniform, arbitrary grids.FFTKDE- A very fast convolution-based computation. Supports weighted d-dimensional data and many kernels, but not variable bandwidth. Must be evaluated on an equidistant grid, the finer the grid the higher the accuracy. Data points may not be outside of the grid.
If you are having trouble using the package, please let me know by creating an Issue on GitHub and I'll get back to you.
Whatever your mathematical and Python background is, you are very welcome to contribute to KDEpy. To contribute, fork the project, create a branch and submit and Pull Request. Please follow these guidelines:
- Import as few external dependencies as possible.
- Use test driven development, have tests and docs for every method.
- Cite literature and implement recent methods.
- Unless it's a bottleneck computation, readability trumps speed.
- Employ object orientation, but resist the temptation to implement many methods -- stick to the basics.
- Follow PEP8.