| orphan: |
|---|
This page covers the definitions of different coordinate systems employed in MNE software and FreeSurfer, the details of the computation of the forward solutions, and the associated low-level utilities.
Coordinate systems in MNE-Python
In some MNE-Python objects (e.g., :class:`~mne.Forward`, :class:`~mne.SourceSpaces`, etc), information about the coordinate frame is encoded as a constant integer value. The meaning of those integers is determined in the source code.
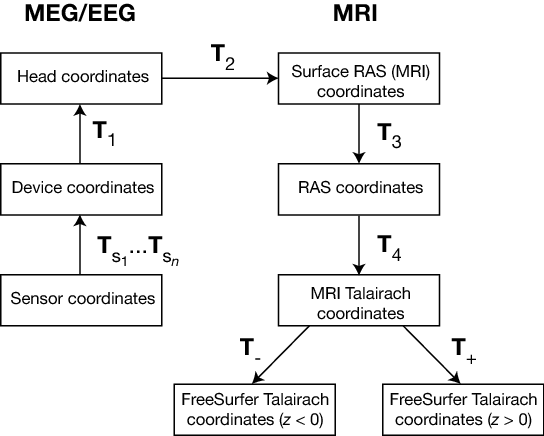
The coordinate systems used in MNE software (and FreeSurfer) and their relationships are depicted in :ref:`coordinate_system_figure`. Except for the sensor coordinates, all of the coordinate systems are Cartesian and have the "RAS" (Right-Anterior-Superior) orientation, i.e., the x axis points to the right, the y axis to the front, and the z axis up.
MEG/EEG and MRI coordinate systems
The coordinate systems related to MEG/EEG data are:
Head coordinates
This is a coordinate system defined with help of the fiducial landmarks (nasion and the two auricular points). In fif files, EEG electrode locations are given in this coordinate system. In addition, the head digitization data acquired in the beginning of an MEG, MEG/EEG, or EEG acquisition are expressed in head coordinates. For details, see :ref:`coordinate_systems`.
Device coordinates
This is a coordinate system tied to the MEG device. The relationship of the Device and Head coordinates is determined during an MEG measurement by feeding current to three to five head-position indicator (HPI) coils and by determining their locations with respect to the MEG sensor array from the magnetic fields they generate.
Sensor coordinates
Each MEG sensor has a local coordinate system defining the orientation and location of the sensor. With help of this coordinate system, the numerical integration data needed for the computation of the magnetic field can be expressed conveniently as discussed in :ref:`coil_geometry_information`. The channel information data in the fif files contain the information to specify the coordinate transformation between the coordinates of each sensor and the MEG device coordinates.
The coordinate systems related to MRI data are:
Surface RAS coordinates
The FreeSurfer surface data are expressed in this coordinate system. The origin of this coordinate system is at the center of the conformed FreeSurfer MRI volumes (usually 256 x 256 x 256 isotropic 1-mm3 voxels) and the axes are oriented along the axes of this volume. The BEM surface and the locations of the sources in the source space are usually expressed in this coordinate system in the fif files. In this manual, the Surface RAS coordinates are usually referred to as MRI coordinates unless there is need to specifically discuss the different MRI-related coordinate systems.
RAS coordinates
This coordinate system has axes identical to the Surface RAS coordinates but the location of the origin is different and defined by the original MRI data, i.e. , the origin is in a scanner-dependent location. There is hardly any need to refer to this coordinate system explicitly in the analysis with the MNE software. However, since the Talairach coordinates, discussed below, are defined with respect to RAS coordinates rather than the Surface RAS coordinates, the RAS coordinate system is implicitly involved in the transformation between Surface RAS coordinates and the two Talairach coordinate systems.
MNI Talairach coordinates
The definition of this coordinate system is discussed, e.g., in https://imaging.mrc-cbu.cam.ac.uk/imaging/MniTalairach. This transformation is determined during the FreeSurfer reconstruction process. These coordinates are in MNI305 space.
FreeSurfer Talairach coordinates
The problem with the MNI Talairach coordinates is that the linear MNI Talairach transform does not match the brains completely to the Talairach brain. This is probably because the Talairach atlas brain is a rather odd shape, and as a result, it is difficult to match a standard brain to the atlas brain using an affine transform. As a result, the MNI brains are slightly larger (in particular higher, deeper and longer) than the Talairach brain. The differences are larger as you get further from the middle of the brain, towards the outside. The FreeSurfer Talairach coordinates mitigate this problem by additing a an additional transformation, defined separately for negatice and positive MNI Talairach z coordinates. These two transformations, denoted by T_- and T_+ in :ref:`coordinate_system_figure`, are fixed as discussed in https://imaging.mrc-cbu.cam.ac.uk/imaging/MniTalairach (Approach 2).
The different coordinate systems are related by coordinate transformations depicted in :ref:`coordinate_system_figure`. The arrows and coordinate transformation symbols (T_x) indicate the transformations actually present in the FreeSurfer files. Generally,
\begin{bmatrix}
x_2 \\
y_2 \\
z_2 \\
1
\end{bmatrix} = T_{12} \begin{bmatrix}
x_1 \\
y_1 \\
z_1 \\
1
\end{bmatrix} = \begin{bmatrix}
R_{11} & R_{12} & R_{13} & x_0 \\
R_{21} & R_{22} & R_{23} & y_0 \\
R_{31} & R_{32} & R_{33} & z_0 \\
0 & 0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x_1 \\
y_1 \\
z_1 \\
1
\end{bmatrix}\ ,
where x_k, y_k,and z_k are the location coordinates in two coordinate systems, T_{12} is the coordinate transformation from coordinate system "1" to "2", x_0, y_0, and z_0 is the location of the origin of coordinate system "1" in coordinate system "2", and R_{jk} are the elements of the rotation matrix relating the two coordinate systems. The coordinate transformations are present in different files produced by FreeSurfer and MNE. The fixed transformations T_- and T_+ are:
T_{-} = \begin{bmatrix}
0.99 & 0 & 0 & 0 \\
0 & 0.9688 & 0.042 & 0 \\
0 & -0.0485 & 0.839 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
and
T_{+} = \begin{bmatrix}
0.99 & 0 & 0 & 0 \\
0 & 0.9688 & 0.046 & 0 \\
0 & -0.0485 & 0.9189 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
Note
This section does not discuss the transformation between the MRI voxel indices and the different MRI coordinates. However, it is important to note that in FreeSurfer, MNE, as well as in Neuromag software an integer voxel coordinate corresponds to the location of the center of a voxel. Detailed information on the FreeSurfer MRI systems can be found at https://surfer.nmr.mgh.harvard.edu/fswiki/CoordinateSystems. The symbols T_x are defined in :ref:`coordinate_system_figure`.
.. tabularcolumns:: |p{0.2\linewidth}|p{0.3\linewidth}|p{0.5\linewidth}|
| Transformation | FreeSurfer | MNE |
| T_1 | Not present | Measurement data files
Forward solution files (
*fwd.fif)Inverse operator files (
*inv.fif) |
| T_{s_1}\dots T_{s_n} | Not present | Channel information in files containing T_1. |
| T_2 | Not present | MRI description filesSeparate
Separate
-trans.fif filesfrom :ref:`mne coreg`
Forward solution files
Inverse operator files
|
| T_3 | mri/*mgz files |
:class:`nibabel.freesurfer.mghformat.MGHImage` |
| T_4 | mri/transforms/talairach.xfm | Internal reading |
| T_- | Hardcoded in software | Hardcoded in software. |
| T_+ | Hardcoded in software | Hardcoded in software. |
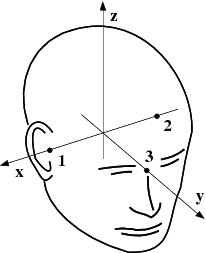
The MEG/EEG head coordinate system employed in the MNE software is a right-handed Cartesian coordinate system. The direction of x axis is from left to right, that of y axis to the front, and the z axis thus points up.
The x axis of the head coordinate system passes through the two periauricular or preauricular points digitized before acquiring the data with positive direction to the right. The y axis passes through the nasion and is normal to the x axis. The z axis points up according to the right-hand rule and is normal to the xy plane.
The origin of the MEG device coordinate system is device dependent. Its origin is located approximately at the center of a sphere which fits the occipital section of the MEG helmet best with x axis axis going from left to right and y axis pointing front. The z axis is, again, normal to the xy plane with positive direction up.
Note
The above definition is identical to that of the Neuromag MEG/EEG (head) coordinate system. However, in 4-D Neuroimaging and CTF MEG systems the head coordinate frame definition is different. The origin of the coordinate system is at the midpoint of the left and right auricular points. The x axis passes through the nasion and the origin with positive direction to the front. The y axis is perpendicular to the x axis on the and lies in the plane defined by the three fiducial landmarks, positive direction from right to left. The z axis is normal to the plane of the landmarks, pointing up. Note that in this convention the auricular points are not necessarily located on y coordinate axis. The file conversion utilities take care of these idiosyncrasies and convert all coordinate information to the MNE software head coordinate frame.
The fif format source space files containing the dipole locations and orientations are created with :func:`mne.setup_source_space`.
In addition to source spaces confined to a surface, the MNE software provides some support for three-dimensional source spaces bounded by a surface as well as source spaces comprised of discrete, arbitrarily located source points. The :func:`mne.setup_volume_source_space` utility assists in generating such source spaces.
See :ref:`bem-model`.
The following topology checks are performed during the creation of BEM models:
- The completeness of each surface is confirmed by calculating the total solid
angle subtended by all triangles from a point inside the triangulation. The
result should be very close to 4 \pi. If the result is -4 \pi
instead, it is conceivable that the ordering of the triangle vertices is
incorrect and the
--swapoption should be specified. - The correct ordering of the surfaces is verified by checking that the surfaces are inside each other as expected. This is accomplished by checking that the sum solid angles subtended by triangles of a surface S_k at all vertices of another surface S_p which is supposed to be inside it equals 4 \pi. Naturally, this check is applied only if the model has more than one surface. Since the surface relations are transitive, it is enough to check that the outer skull surface is inside the skin surface and that the inner skull surface is inside the outer skull one.
- The extent of each of the triangulated volumes is checked. If the extent is smaller than 50mm, an error is reported. This may indicate that the vertex coordinates have been specified in meters instead of millimeters.
The utility :func:`mne.make_bem_solution` computes the geometry information for BEM.
This Section explains the presentation of MEG detection coil geometry information the approximations used for different detection coils in MNE software. Two pieces of information are needed to characterize the detectors:
- The location and orientation a local coordinate system for each detector.
- A unique identifier, which has an one-to-one correspondence to the geometrical description of the coil.
Note
MNE ships with several coil geometry configurations. They can be
found in mne/data. See :ref:`ex-plot-meg-sensors` for a
comparison between different coil geometries, and
:ref:`implemented_coil_geometries` for detailed information regarding
the files describing Neuromag coil geometries.
The sensor coordinate system is completely characterized by the location of its origin and the direction cosines of three orthogonal unit vectors pointing to the directions of the x, y, and z axis. In fact, the unit vectors contain redundant information because the orientation can be uniquely defined with three angles. The measurement fif files list these data in MEG device coordinates. Transformation to the MEG head coordinate frame can be easily accomplished by applying the device-to-head coordinate transformation matrix available in the data files provided that the head-position indicator was used. Optionally, the MNE software forward calculation applies another coordinate transformation to the head-coordinate data to bring the coil locations and orientations to the MRI coordinate system.
If r_0 is a row vector for the origin of the local sensor coordinate system and e_x, e_y, and e_z are the row vectors for the three orthogonal unit vectors, all given in device coordinates, a location of a point r_C in sensor coordinates is transformed to device coordinates (r_D) by
[r_D 1] = [r_C 1] T_{CD}\ ,
where
T = \begin{bmatrix}
e_x & 0 \\
e_y & 0 \\
e_z & 0 \\
r_{0D} & 1
\end{bmatrix}\ .
The forward calculation in the MNE software computes the signals detected by each MEG sensor for three orthogonal dipoles at each source space location. This requires specification of the conductor model, the location and orientation of the dipoles, and the location and orientation of each MEG sensor as well as its coil geometry.
The output of each SQUID sensor is a weighted sum of the magnetic fluxes threading the loops comprising the detection coil. Since the flux threading a coil loop is an integral of the magnetic field component normal to the coil plane, the output of the k th MEG channel, b_k can be approximated by:
b_k = \sum_{p = 1}^{N_k} {w_{kp} B(r_{kp}) \cdot n_{kp}}
where r_{kp} are a set of N_k integration points covering the pickup coil loops of the sensor, B(r_{kp}) is the magnetic field due to the current sources calculated at r_{kp}, n_{kp} are the coil normal directions at these points, and w_{kp} are the weights associated to the integration points. This formula essentially presents numerical integration of the magnetic field over the pickup loops of sensor k.
There are three accuracy levels for the numerical integration expressed above.
The simple accuracy means the simplest description of the coil. This accuracy
is not used in the MNE forward calculations. The normal or recommended
accuracy typically uses two integration points for planar gradiometers, one in
each half of the pickup coil and four evenly distributed integration points for
magnetometers. This is the default accuracy used by MNE. If the --accurate
option is specified, the forward calculation typically employs a total of eight
integration points for planar gradiometers and sixteen for magnetometers.
Detailed information about the integration points is given in the next section.
This section describes the coil geometries currently implemented in MNE. The coil types fall in two general categories:
- Axial gradiometers and planar gradiometers and
- Planar magnetometers.
For axial sensors, the z axis of the local coordinate system is parallel to the field component detected, i.e., normal to the coil plane.For circular coils, the orientation of the x and y axes on the plane normal to the z axis is irrelevant. In the square coils employed in the Vectorview (TM) system the x axis is chosen to be parallel to one of the sides of the magnetometer coil. For planar sensors, the z axis is likewise normal to the coil plane and the x axis passes through the centerpoints of the two coil loops so that the detector gives a positive signal when the normal field component increases along the x axis.
:ref:`normal_coil_descriptions` lists the parameters of the normal coil geometry descriptions :ref:`accurate_coil_descriptions` lists the accurate descriptions. For simple accuracy, please consult the coil definition file, see :ref:`coil_definition_file`. The columns of the tables contain the following data:
- The number identifying the coil id. This number is used in the coil descriptions found in the FIF files.
- Description of the coil.
- Number of integration points used
- The locations of the integration points in sensor coordinates.
- Weights assigned to the field values at the integration points. Some formulas are listed instead of the numerical values to demonstrate the principle of the calculation. For example, in the normal coil descriptions of the planar gradiometers the weights are inverses of the baseline of the gradiometer to show that the output is in T/m.
Note
The coil geometry information is stored in the file
:file:`mne/data/coil_def.dat`, which is
automatically created by the MNE-C utility mne_list_coil_def.
.. tabularcolumns:: |p{0.1\linewidth}|p{0.3\linewidth}|p{0.1\linewidth}|p{0.25\linewidth}|p{0.2\linewidth}|
| Id | Description | n | r/mm | w |
|---|---|---|---|---|
| 2 | Neuromag-122 planar gradiometer | 2 | (+/-8.1, 0, 0) mm | +/-1 ⁄ 16.2mm |
| 2000 | A point magnetometer | 1 | (0, 0, 0)mm | 1 |
| 3012 | Vectorview type 1 planar gradiometer | 2 | (+/-8.4, 0, 0.3) mm | +/-1 ⁄ 16.8mm |
| 3013 | Vectorview type 2 planar gradiometer | 2 | (+/-8.4, 0, 0.3) mm | +/-1 ⁄ 16.8mm |
| 3022 | Vectorview type 1 magnetometer | 4 | (+/-6.45, +/-6.45, 0.3)mm | 1/4 |
| 3023 | Vectorview type 2 magnetometer | 4 | (+/-6.45, +/-6.45, 0.3)mm | 1/4 |
| 3024 | Vectorview type 3 magnetometer | 4 | (+/-5.25, +/-5.25, 0.3)mm | 1/4 |
| 2000 | An ideal point magnetometer | 1 | (0.0, 0.0, 0.0)mm | 1 |
| 4001 | Magnes WH magnetometer | 4 | (+/-5.75, +/-5.75, 0.0)mm | 1/4 |
| 4002 | Magnes WH 3600 axial gradiometer | 8 | (+/-4.5, +/-4.5, 0.0)mm (+/-4.5, +/-4.5, 50.0)mm | 1/4 -1/4 |
| 4003 | Magnes reference magnetometer | 4 | (+/-7.5, +/-7.5, 0.0)mm | 1/4 |
| 4004 | Magnes reference gradiometer measuring diagonal gradients | 8 | (+/-20, +/-20, 0.0)mm (+/-20, +/-20, 135)mm | 1/4 -1/4 |
| 4005 | Magnes reference gradiometer measuring off-diagonal gradients | 8 | (87.5, +/-20, 0.0)mm (47.5, +/-20, 0.0)mm (-87.5, +/-20, 0.0)mm (-47.5, +/-20, 0.0)mm | 1/4 -1/4 1/4 -1/4 |
| 5001 | CTF 275 axial gradiometer | 8 | (+/-4.5, +/-4.5, 0.0)mm (+/-4.5, +/-4.5, 50.0)mm | 1/4 -1/4 |
| 5002 | CTF reference magnetometer | 4 | (+/-4, +/-4, 0.0)mm | 1/4 |
| 5003 | CTF reference gradiometer measuring diagonal gradients | 8 | (+/-8.6, +/-8.6, 0.0)mm (+/-8.6, +/-8.6, 78.6)mm | 1/4 -1/4 |
Note
If a plus-minus sign occurs in several coordinates, all possible combinations have to be included.
.. tabularcolumns:: |p{0.1\linewidth}|p{0.3\linewidth}|p{0.05\linewidth}|p{0.25\linewidth}|p{0.15\linewidth}|
| Id | Description | n | r/mm | w |
|---|---|---|---|---|
| 2 | Neuromag-122 planar gradiometer | 8 | +/-(8.1, 0, 0) mm | +/-1 ⁄ 16.2mm |
| 2000 | A point magnetometer | 1 | (0, 0, 0) mm | 1 |
| 3012 | Vectorview type 1 planar gradiometer | 2 | (+/-8.4, 0, 0.3) mm | +/-1 ⁄ 16.8mm |
| 3013 | Vectorview type 2 planar gradiometer | 2 | (+/-8.4, 0, 0.3) mm | +/-1 ⁄ 16.8mm |
| 3022 | Vectorview type 1 magnetometer | 4 | (+/-6.45, +/-6.45, 0.3)mm | 1/4 |
| 3023 | Vectorview type 2 magnetometer | 4 | (+/-6.45, +/-6.45, 0.3)mm | 1/4 |
| 3024 | Vectorview type 3 magnetometer | 4 | (+/-5.25, +/-5.25, 0.3)mm | 1/4 |
| 4001 | Magnes WH magnetometer | 4 | (+/-5.75, +/-5.75, 0.0)mm | 1/4 |
| 4002 | Magnes WH 3600 axial gradiometer | 4 | (+/-4.5, +/-4.5, 0.0)mm (+/-4.5, +/-4.5, 0.0)mm | 1/4 -1/4 |
| 4004 | Magnes reference gradiometer measuring diagonal gradients | 8 | (+/-20, +/-20, 0.0)mm (+/-20, +/-20, 135)mm | 1/4 -1/4 |
| 4005 | Magnes reference gradiometer measuring off-diagonal gradients | 8 | (87.5, +/-20, 0.0)mm (47.5, +/-20, 0.0)mm (-87.5, +/-20, 0.0)mm (-47.5, +/-20, 0.0)mm | 1/4 -1/4 1/4 -1/4 |
| 5001 | CTF 275 axial gradiometer | 8 | (+/-4.5, +/-4.5, 0.0)mm (+/-4.5, +/-4.5, 50.0)mm | 1/4 -1/4 |
| 5002 | CTF reference magnetometer | 4 | (+/-4, +/-4, 0.0)mm | 1/4 |
| 5003 | CTF 275 reference gradiometer measuring diagonal gradients | 8 | (+/-8.6, +/-8.6, 0.0)mm (+/-8.6, +/-8.6, 78.6)mm | 1/4 -1/4 |
| 5004 | CTF 275 reference gradiometer measuring off-diagonal gradients | 8 | (47.8, +/-8.5, 0.0)mm (30.8, +/-8.5, 0.0)mm (-47.8, +/-8.5, 0.0)mm (-30.8, +/-8.5, 0.0)mm | 1/4 -1/4 1/4 -1/4 |
| 6001 | MIT KIT system axial gradiometer | 8 | (+/-3.875, +/-3.875, 0.0)mm (+/-3.875, +/-3.875, 0.0)mm | 1/4 -1/4 |
The coil geometry information is stored in the text file :file:`{$MNE_ROOT}/share/mne/coil_def.dat`. In this file, any lines starting with the pound sign (#) are comments. A coil definition starts with a description line containing the following fields:
- :samp:`{<class>}`: A number indicating class of this coil.
- :samp:`{<id>}`: Coil ID value. This value is listed in the first column of Tables :ref:`normal_coil_descriptions` and :ref:`accurate_coil_descriptions`.
- :samp:`{<accuracy>}`: The coil representation accuracy. Possible values and their meanings are listed in :ref:`coil_accuracies`.
- :samp:`{<np>}`: Number of integration points in this representation.
- :samp:`{<size/m>}`: The size of the coil. For circular coils this is the diameter of the coil and for square ones the side length of the square. This information is mainly included to facilitate drawing of the coil geometry. It should not be employed to infer a coil approximation for the forward calculations.
- :samp:`{<baseline/m>}`: The baseline of a this kind of a coil. This will be zero for magnetometer coils. This information is mainly included to facilitate drawing of the coil geometry. It should not be employed to infer a coil approximation for the forward calculations.
- :samp:`{<description>}`: Short description of this kind of a coil. If the description contains several words, it is enclosed in quotes.
.. tabularcolumns:: |p{0.1\linewidth}|p{0.5\linewidth}|
| Value | Meaning |
|---|---|
| 1 | The simplest representation available |
| 2 | The standard or normal representation (see :ref:`normal_coil_descriptions`) |
| 3 | The most accurate representation available (see :ref:`accurate_coil_descriptions`) |
Each coil description line is followed by one or more integration point lines, consisting of seven numbers:
- :samp:`{<weight>}`: Gives the weight for this integration point (last column in Tables :ref:`normal_coil_descriptions` and :ref:`accurate_coil_descriptions`).
- :samp:`{<x/m>} {<y/m>} {<z/m>}`: Indicates the location of the integration point (fourth column in Tables :ref:`normal_coil_descriptions` and :ref:`accurate_coil_descriptions`).
- :samp:`{<nx>} {<ny>} {<nz>}`: Components of a unit vector indicating the field component to be selected. Note that listing a separate unit vector for each integration points allows the implementation of curved coils and coils with the gradiometer loops tilted with respect to each other.
Examples on how to compute the forward solution in MNE-Python using :func:`mne.make_forward_solution` can be found :ref:`plot_forward_compute_forward_solution` and :ref:`computing_the_forward_solution`.
Accounting for noise cancellation in MNE-Python is accomplished in :meth:`mne.io.Raw.apply_gradient_compensation`. See :ref:`plot_brainstorm_phantom_ctf` for an example.
CTF and 4D Neuroimaging data may have been subjected to noise cancellation employing the data from the reference sensor array. Even though these sensor are rather far away from the brain sources, :func:`mne.make_forward_solution` takes them into account in the computations. If the data file has software gradient compensation activated, it computes the field of at the reference sensors in addition to the main MEG sensor array and computes a compensated forward solution.
In MNE-Python, different sphere models can be specified through :func:`mne.make_sphere_model`. The default model has the following structure:
.. tabularcolumns:: |p{0.1\linewidth}|p{0.25\linewidth}|p{0.2\linewidth}|
| Layer | Relative outer radius | \sigma (S/m) |
|---|---|---|
| Head | 1.0 | 0.33 |
| Skull | 0.97 | 0.04 |
| CSF | 0.92 | 1.0 |
| Brain | 0.90 | 0.33 |
Although it is not BEM model per se the sphere structure describes the head
geometry so it can be passed as bem parameter in MNE-Python functions such
as :func:`mne.fit_dipole`, :func:`mne.viz.plot_alignment` or
:func:`mne.make_forward_solution`.
Sphere-model examples in MNE-Python
For examples of using the sphere model when computing the forward model (using :func:`mne.make_forward_solution`), see :ref:`Brainstorm CTF phantom dataset tutorial <plt_brainstorm_phantom_ctf_eeg_sphere_geometry>`, :ref:`Brainstorm Elekta phantom dataset tutorial <plt_brainstorm_phantom_elekta_eeg_sphere_geometry>`, and :ref:`tut-source-alignment-without-mri`.
When the sphere model is employed, the computation of the EEG solution can be substantially accelerated by using approximation methods described by Mosher :footcite:`MosherEtAl1999`, Zhang :footcite:`Zhang1995`, and Berg :footcite:`BergScherg1994`. :func:`mne.make_forward_solution` approximates the solution with three dipoles in a homogeneous sphere whose locations and amplitudes are determined by minimizing the cost function:
S(r_1,\dotsc,r_m\ ,\ \mu_1,\dotsc,\mu_m) = \int_{scalp} {(V_{true} - V_{approx})}\,dS
where r_1,\dotsc,r_m and \mu_1,\dotsc,\mu_m are the locations and amplitudes of the approximating dipoles and V_{true} and V_{approx} are the potential distributions given by the true and approximative formulas, respectively. It can be shown that this integral can be expressed in closed form using an expansion of the potentials in spherical harmonics. The formula is evaluated for the most superficial dipoles, i.e., those lying just inside the inner skull surface.
One possibility to make a grand average over several runs of a experiment is to average the data across runs and average the forward solutions accordingly. For this purpose, :func:`mne.average_forward_solutions` computes a weighted average of several forward solutions. The function averages both MEG and EEG forward solutions. Usually the EEG forward solution is identical across runs because the electrode locations do not change.