https://leetcode.com/problems/container-with-most-water/description/
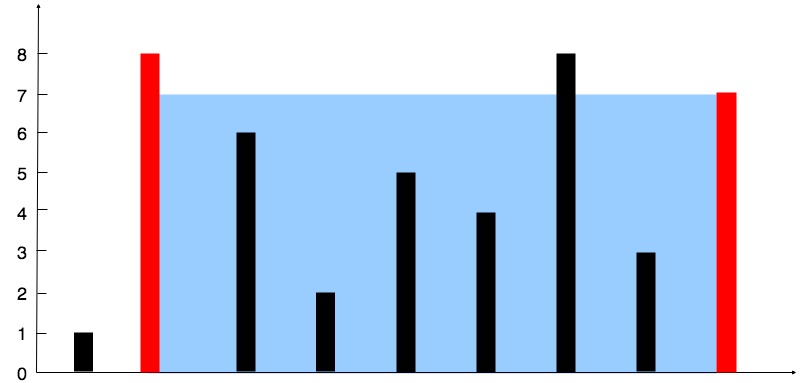
Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
- 双指针
符合直觉的解法是,我们可以对两两进行求解,计算可以承载的水量。 然后不断更新最大值,最后返回最大值即可。 这种解法,需要两层循环,时间复杂度是 O(n^2)
eg:
// 这个解法比较暴力,效率比较低
// 时间复杂度是O(n^2)
let max = 0;
for (let i = 0; i < height.length; i++) {
for (let j = i + 1; j < height.length; j++) {
const currentArea = Math.abs(i - j) * Math.min(height[i], height[j]);
if (currentArea > max) {
max = currentArea;
}
}
}
return max;这种符合直觉的解法有点像冒泡排序, 大家可以稍微类比一下
那么有没有更加优的解法呢?我们来换个角度来思考这个问题,上述的解法是通过两两组合,这无疑是完备的, 那我门是否可以先计算长度为 n 的面积,然后计算长度为 n-1 的面积,... 计算长度为 1 的面积。 这样去不断更新最大值呢? 很显然这种解法也是完备的,但是似乎时间复杂度还是 O(n ^ 2), 不要着急。
考虑一下,如果我们计算 n-1 长度的面积的时候,是直接直接排除一半的结果的。
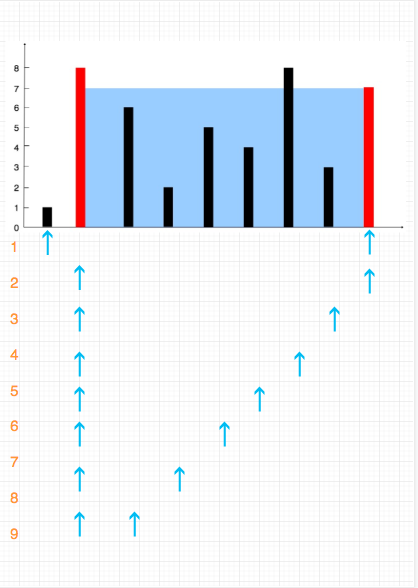
如图:
比如我们计算 n 面积的时候,假如左侧的线段高度比右侧的高度低,那么我们通过左移右指针来将长度缩短为 n-1 的做法是没有意义的,
因为新的形成的面积变成了(n-1) * heightOfLeft 这个面积一定比刚才的长度为n的面积nn * heightOfLeft 小
也就是说最大面积一定是当前的面积或者通过移动短的线段得到。
- 双指针优化时间复杂度
- 语言支持:JS,C++
JavaScript Code:
/**
* @param {number[]} height
* @return {number}
*/
var maxArea = function (height) {
if (!height || height.length <= 1) return 0;
let leftPos = 0;
let rightPos = height.length - 1;
let max = 0;
while (leftPos < rightPos) {
const currentArea =
Math.abs(leftPos - rightPos) *
Math.min(height[leftPos], height[rightPos]);
if (currentArea > max) {
max = currentArea;
}
// 更新小的
if (height[leftPos] < height[rightPos]) {
leftPos++;
} else {
// 如果相等就随便了
rightPos--;
}
}
return max;
};C++ Code:
class Solution {
public:
int maxArea(vector<int>& height) {
auto ret = 0ul, leftPos = 0ul, rightPos = height.size() - 1;
while( leftPos < rightPos)
{
ret = std::max(ret, std::min(height[leftPos], height[rightPos]) * (rightPos - leftPos));
if (height[leftPos] < height[rightPos]) ++leftPos;
else --rightPos;
}
return ret;
}
};复杂度分析
- 时间复杂度:$O(N)$
- 空间复杂度:$O(1)$
大家也可以关注我的公众号《脑洞前端》获取更多更新鲜的 LeetCode 题解