Proof Aggregation

Mechanism

Aggregation allows larger amounts of data to be verified on-chain using fewer proofs. Currently, chunks (a list of continuous blocks) are first aggregated into a batch, then multiple batches are aggregated using a recursive scheme into a bundle. The bundle is the current apex entity that will be verified on-chain.

Params

param	meaning
k	number of valid chunks
n	max number of chunks per batch (hard-coded)
t	number of rounds for the final hash $\lceil32\times n/136\rceil$

Structs

Chunk

A chunk is a list of L2 blocks and will be proven by the ChunkCircuit (this is in fact the ZkEVM SuperCircuit). It consists of 5 hashes:

• state root before this chunk
• state root after this chunk
• the withdraw root of this chunk
• the data hash of this chunk
• the tx data hash of this chunk

Those 5 hashes are obtained from the caller.

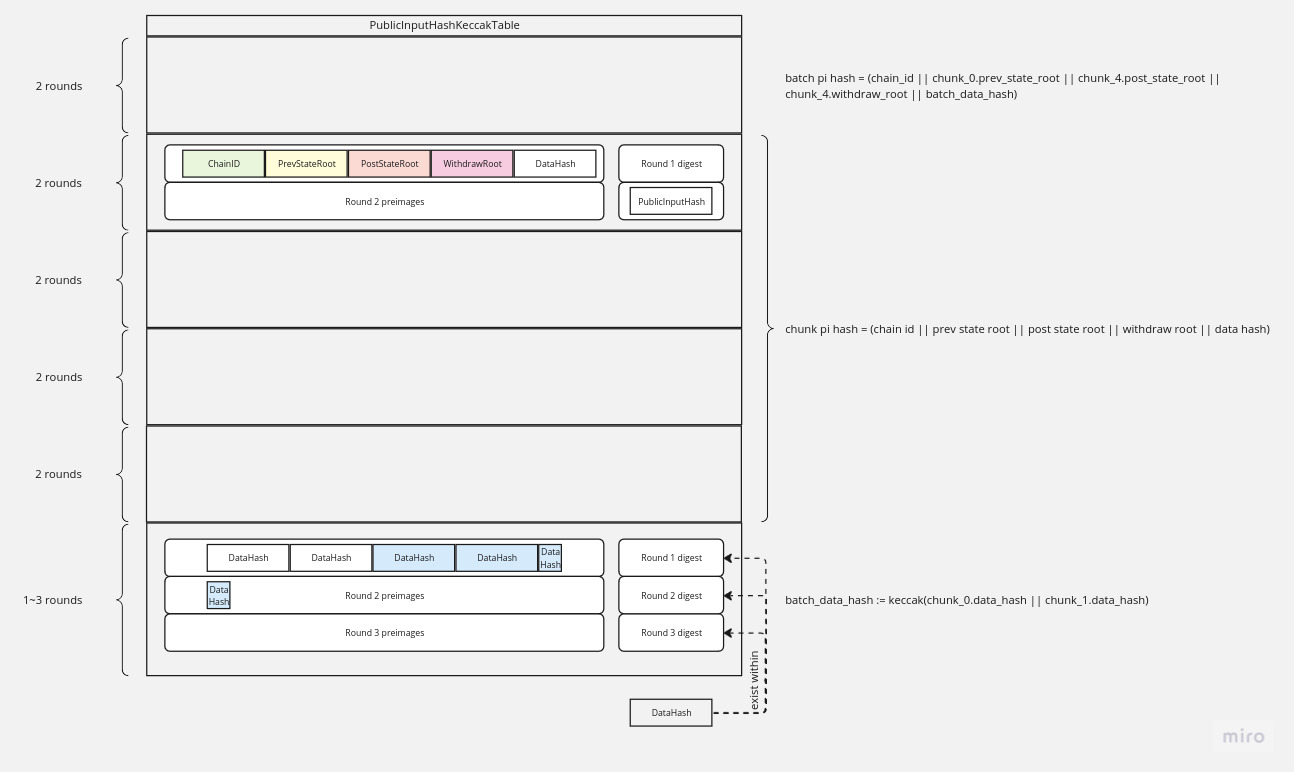
The chunk's public input hash is

chunk_pi_hash := keccak(chain_id || prev_state_root || post_state_root || withdraw_root ||  chunk_data_hash || chunk_txdata_hash)

Continuous chunks

A list of continuous chunks $c_1, \dots, c_k$ satisfy

c_i.post_state_root == c_{i+1}.prev_state_root

for $i \in [1, k-1]$.

Padded chunk

A padded chunk is a chunk that repeats the last valid chunk. It is used for padding. If $k< n$, $(n-k)$ padded chunks are padded to the list. A padded chunk has the same data fields as the last real chunk, and the parameters are set as

• state root before this chunk: c_{k}.prev_state_root
• state root after this chunk: c_{k}.post_state_root
• the withdraw root of this chunk: c_{k}.withdraw_root
• the data hash of this chunk: c_{k}.data_hash
• the tx data hash of this chunk: c_{k}.txdata_hash

Batch

A batch is a list of continuous chunks of size k that will be aggregated using the BatchCircuit. If the input chunks' size k is less than n, we pad the input with (n-k) chunks identical to chunk[k]. The batch is represented by the preimage fields to the batch_hash, which is constructed as:

batchHash := keccak256(version || batch_index || l1_message_popped || total_l1_message_popped || batch_data_hash || versioned_hash || parent_batch_hash || last_block_timestamp || z || y)

All preimage fields' values are provided to the batch through the BatchHeader struct, so it can correctly construct the hash state transition from parent_batch_hash to batch_hash (for current batch).

Note that there are also implicit constraints between state roots before/after batch and the state roots of the chunks it has aggregated:

prev_state_root := c_0.prev_state_root
post_state_root := c_k.post_state_root

BatchHeader

The current schema for batch header is:

Field	Bytes	Type	Index	Comments
version	1	uint8	0	The batch version
batchIndex	8	uint64	1	The index of the batch
l1MessagePopped	8	uint64	9	Number of L1 messages popped in the batch
totalL1MessagePopped	8	uint64	17	Number of total L1 messages popped after the batch
dataHash	32	bytes32	25	The data hash of the batch
blobVersionedHash	32	bytes32	57	The versioned hash of the blob with this batch’s data
parentBatchHash	32	bytes32	89	The parent batch hash
lastBlockTimestamp	8	uint64	121	The timestamp of the last block in this batch
blobDataProof	64	bytes64	129	The blob data proof: z (32), y (32)

Continuous batches

A list of continuous batches $b_1, \dots, b_k$ satisfy

b_i.batch_hash == b_{i+1}.parent_batch_hash AND
b_i.post_state_root == b_{i+1}.prev_state_root

for $i \in [1, k-1]$. Unlike chunks aggregation, the last layer of recursive batch aggregation can accept an arbitrary number of batches. There's no explicit upper limit. Instead, the number of rounds of recursion can solely be defined by the latency target on L1 for those batches. As a result, continuous batches are never padded.

Bundle

A bundle is a list of continuous batches that will be aggregated recursively using the RecursionCircuit. The bundle is the current apex entity whose proof will be verified on-chain.

Circuits

Chunk circuit

Circuit proving the relationship for a chunk is the zkEVM circuit. It will go through 2 layers of compression circuit, and becomes a snark struct. We do not list its details here. Abstractly, a snark circuit has the following properties:

• it takes 44 elements as public inputs
  • 12 from accumulators
  • 32 from public input hash

Batch Circuit

We want to aggregate k snarks, each from a valid chunk. We generate (n-k) padded chunks (by repeating the last non-padding chunk), and obtain a total of n snarks. Additionally, the batch circuit has to ascertain the correct hash transition from the parent batch.

Configuration

There are several configuration subcomponents for batch circuit.

• FpConfig; used for snark aggregation.
• KeccakConfig: used to build keccak table.
• RlcConfig: used to compute RLC of hash inputs.
• BlobDataConfig: used for representing the zstd-encoded form of batch data, with 4096 * 31 rows. Each row is a byte value. An EIP-4844 blob consists of 4096 * 32 bytes, where we set the most-significant byte in each 32-bytes chunk as 0 to guarantee that each 32-bytes chunk is a valid BLS12-381 scalar field element.
• BatchDataConfig: used for representing the raw batch bytes, effectively constructing the random challenge point z for the KZG opening proof.
• DecoderConfig: implements an in-circuit zstd-decoder that decodes blob data into batch data
• BarycentricEvaluationConfig: used for evaluating the interpolated blob polynomial at an arbitrary challenge point z, where both z and the evaluation y are included in the BatchHeader.

Public Input

The public input of the batch circuit consists of

• 12 elements from accumulator
• 2 elements of parent_state_root (split by hi/lo)
• 2 elements of parent_batch_hash
• 2 elements of current_state_root
• 2 elements of current_batch_hash
• 1 element of chain_id
• 2 elements of current_withdraw_root

Note that parent_state_root is the same as chunk[0].prev_state_root and current_state_root is the same as chunk[k].post_state_root. When these chunk fields are assigned into keccak preimages, their cells are constrained against the public input to ensure equality. If any public input appears in the preimage of the batch_hash, their corresponding assigned preimage cells will be equality constrained as well.

Statements

For snarks $s_1,\dots,s_k,\dots, s_n$ the batch circuit argues the following statements.

1. batch_data_hash digest is reused for batch hash. Static.

2. batch_data_hash and chunk[i].pi_hash use a same chunk[i].data_hash when chunk[i] is not padded

for i in 1 ... n
    chunk_pi_hash   := keccak(chain_id || prev_state_root || post_state_root || withdraw_root || chunk_data_hash || chunk_txdata_hash)

This is done by computing the RLCs of chunk[i]'s data_hash for i=0..k, and then check the RLC matches the one from the keccak table.

3. chunks are continuous when they are not padded: they are linked via the state roots.

for i in 1 ... k-1
    c_i.post_state_root == c_{i+1}.prev_state_root

4. All the chunks use the same chain id. Static.

for i in 1 ... n
    batch.chain_id == chunk[i].chain_id

5. The last (n-k) chunk[i] are padded chunks

for i in 1 ... n:
    if is_padding:
        chunk[i]'s chunk_pi_hash_rlc_cells == chunk[i-1].chunk_pi_hash_rlc_cells

This is done via comparing the data_rlc of chunk_{i-1} and chunk_{i}. 6. the hash input length is correct

• hashes[0] has 193 bytes (batch_hash preimage)
• hashes[1..N_SNARKS+1] has 168 bytes input (chunk_pi_hash preimages)
• batch's data_hash length is 32 * number_of_valid_snarks (batch_data_hash preimage)

Handling dynamic inputs

Our keccak table uses $2^{19}$ rows. Each keccak round takes 300 rows. When the number of round is less than $2^{19}/300$, the cell manager will fill in the rest of the rows with dummy hashes.

The only hash that uses a dynamic number of rounds is the last hash. Suppose we target for MAX_AGG_SNARK = 10. Then, the last hash function will take no more than 32 * 10 /136 = 3 rounds.

We also know in the circuit if a chunk is an empty one or not. This is given by a flag is_padding.

For the input of the final data hash

• we extract 32 * MAX_AGG_SNARK number of cells (static here) from the last hash. We then compute the RLC of those 32 * MAX_AGG_SNARK when the corresponding is_padding is not set. We constrain this RLC match the data_rlc from the keccak table.

For the output of the final data hash

• we extract all three hash digest cells from the last 3 rounds. We then constraint that the actual data hash matches one of the three hash digest cells with proper flags defined as follows.
  • if the num_of_valid_snarks <= 4, which only needs 1 keccak-f round. Therefore the batch's data hash (input, len, data_rlc, output_rlc) is in the first 300 keccak rows;
  • else if the num_of_valid_snarks <= 8, which needs 2 keccak-f rounds. Therefore the batch's data hash (input, len, data_rlc, output_rlc) is in the 2nd 300 keccak rows;
  • else the num_of_valid_snarks <= 12, which needs 3 keccak-f rounds. Therefore the batch's data hash (input, len, data_rlc, output_rlc) is in the 3rd 300 keccak rows;

#valid snarks	offset of data hash	flags
1,2,3,4	0	1, 0, 0
5,6,7,8	32	0, 1, 0
9,10	64	0, 0, 1

Additional checks for dummy chunk

• if is_padding for i-th chunk, we constrain chunk[i]'s chunk_pi_hash_rlc_cells == chunk[i-1].chunk_pi_hash_rlc_cells

Recursion Circuit

RecursionCircuit aggregates $N$ SNARKs from a generic circuit (called AppCircuit). It achieves this aggregation by repeatedly combine each AppCircuit's SNARK with a SNARK generated from last round of aggregation (hence the name recursion). In each round of recursion, the Recursion circuit verifies a SNARK from the AppCircuit and its SNARK from the “previous” round. For the first round of aggregation, a dummy SNARK is generated to combine with the first AppCircuit SNARK. Essentially, we have:

$RC_{Snark}(N) \colonequals verify(App_{Snark}(N)) \bigvee verify(RC_{Snark}(N-1))$

where $RC$ indicates the Recursion circuit. With accumulator_indices , Recursion Circuit can merge AppCircuit ’s accumulator, in case AppCircuit itself is also a Batch Circuit.

StateTransition Trait

The AppCircuit must follow a layout that RecursionCircuit accepts. The layout is described in the StateTransition trait which describes a data which can transition from prev state to current state, with methods clearly indicating the indices of accumulators, states (prev and post) and additional exported PI fields.

pub trait StateTransition: Sized {
    type Input: Clone;
    type Circuit: CircuitExt<Fr>;

    // Describes the state transition
    fn state_transition(&self, round: usize) -> Self::Input;

    // Count of the fields used to represent state. The public input consists of twice
    // this number as both the previous and current states are included in the public input.
    fn num_transition_instance() -> usize

    // Other counts of instance variables
    fn num_additional_instance() -> usize
    fn num_instance() -> usize
    fn num_accumulator_instance() -> usize

    // Location of accumulator, state variables and additional exported PIs
    fn accumulator_indices() -> Vec<usize>
    fn state_prev_indices() -> Vec<usize>
    fn state_indices() -> Vec<usize>
    fn additional_indices() -> Vec<usize>
    fn propagate_indices() -> Vec<usize>
}

Public Inputs

All parts of $PI$ in AppCircuit is also put into the $PI$ of recursion circuit, the recursion circuit has a single column of $PI$ with following layout:

`accumulator` | `preprocessed_digest` | `init_states` | `final_states` | `propagated_additional_states` | `additional_states` | `round`

• accumulator accumulates all of the accumulators from the $N$ $snark_{app}$, all the accumulators exported from the $PI$ of these snarks (if there is any), and accumulators generated by the $N$ steps verification of snarks from recursion circuit.
• preprocessed_digest represents the Recursion Circuit itself. There would be an unique value for every recursion circuit which can bundle (any number of) snarks from specified AppCircuit
• init_states represent the initial state $S_0$.
• final_states represent the final state, along with the exported $PI$ from $S_N$.
• propagated_additional_states represent PIs in app states which do not involved in state transition, however, the PIs in recursion circuit must be "propagated" into the corresponding PI in every app circuit being verified recursively. For example, the PI of chainID in each batch circuit must be same when they are verified together in the recursion circuit
• additional_states represent the PIs in app state which do not involved in state transition, and only the PIs in the last app circuit for this part are "export" transparently.
• round represents the number of batches being bundled recursively, i.e. $N$.

Statements

To verify the $k_{th}$ snark, we have 3 PIs from the current circuit, the snark of $k_{th}$ AppCircuit , and the snark of $(k-1){th}$ recursion circuit respectively. We named it $PI$, $PI{app}$ and $PI_{prev}$. We have following equality constraints for them:

• if $N &gt; 0$, $PI(preprocessed_digest) = PI_{prev}(preprocessed_digest)$: ensure the snark for “previous recursion circuit” is the same circuit of current one
• if $N &gt; 0$, $PI(round) = PI_{prev}(round) + 1$: ensure the round number is increment so the first snark from app circuit has round = 0
• if $N &gt; 0$, $PI(init_states) = PI_{prev}(init_states)$, else $PI(init_states) = PI_{app}(init_states)$: propagate the init state, and for first recursion, the init state part of PI is passed to app circuit
• $PI_{app}(final_states) = PI(final_states)$: transparent pass the PIs in final_states to app circuit
• $PI_{app}(all_additional_states) = PI(all_additional_states)$: ensure the PIs in propagated_additional_states and additional_states would be passed to app circuit's PI fields, which are being marked by additional_indices
• if $N &gt; 0$, $PI_{app}(propagated_additional_states) = PI_{prev}(propagated_additional_states)$: propagate the additional state being marked by propagate_indices
• $PI_{app}(init_states) = PI_{prev}(final_states)$: the init state part of PI for app circuit must be “chained” with previous recursion round