The previous two chapters covered some fundamental math. We learned how Finite Fields work and we also learned what an Elliptic Curve is. In this chapter, we’re going to combine the two concepts to get Elliptic Curve Cryptography. Specifically, we’re going to build the primitives needed to sign and verify messages, which is at the heart of what Bitcoin does.
We discussed in the last chapter what an Elliptic curve looks like visually because we were plotting the curve over real numbers. Specifically, it’s not just integers or even rational numbers, but all real numbers. Pi, sqrt(2), e+7th root of 19, etc are all part of real numbers.
What’s interesting is that real numbers are also a field. Note unlike a finite field, there are an infinite number of real numbers, but otherwise the same properties hold:
-
if a and b are in the set, a+b and a⋅b is in the set. We call this property closed
-
The additive identity, 0 exists. This means a + 0 = a
-
The multiplicative identity, 1 exists. This means a ⋅ 1 = a
-
If a is in the set, -a is in the set. -a is defined as the value that makes a + (-a) = 0. This is what we call the additive inverse.
-
If a is in the set and is not 0, a-1 is in the set. a-1 is defined as the value that makes a ⋅ a-1 = 1. This is what we call the multiplicative inverse.
Clearly, all of these are true as normal addition and multiplication apply for the first part, additive and multiplicative identities 0 and 1 exist, -x is the additive inverse and 1/x is the multiplicative inverse. Normal math applies to everything here.
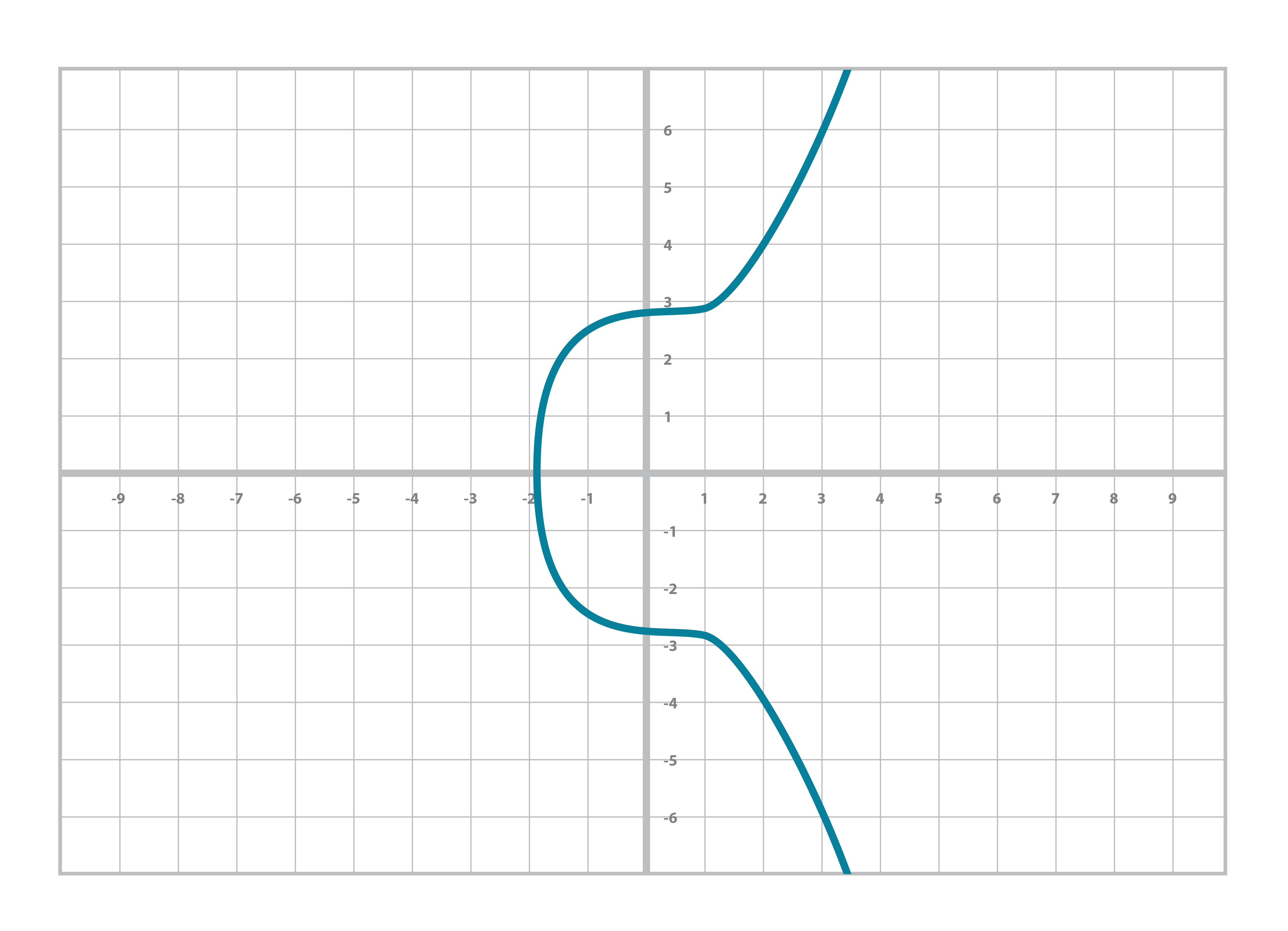
The nice thing about real numbers is that we can easily plot what’s going on and see the whole thing visually as we did in the last chapter. For example, y2=x3+7 can be plotted like this:
What’s interesting is that we can use this equation over any field, including the Finite Fields we explored in Chapter 1. The only difference is that we have to use the addition/subtraction/multiplication/division as we defined them, not the "normal" versions that the real numbers use.
For example, we can see what to do for the equation y2=x3+7 over F103. Let’s see if the point (17,64) is on the curve:
642%103=79 (173+7)%103=79
Indeed, that point is on the curve using the Finite Field math.
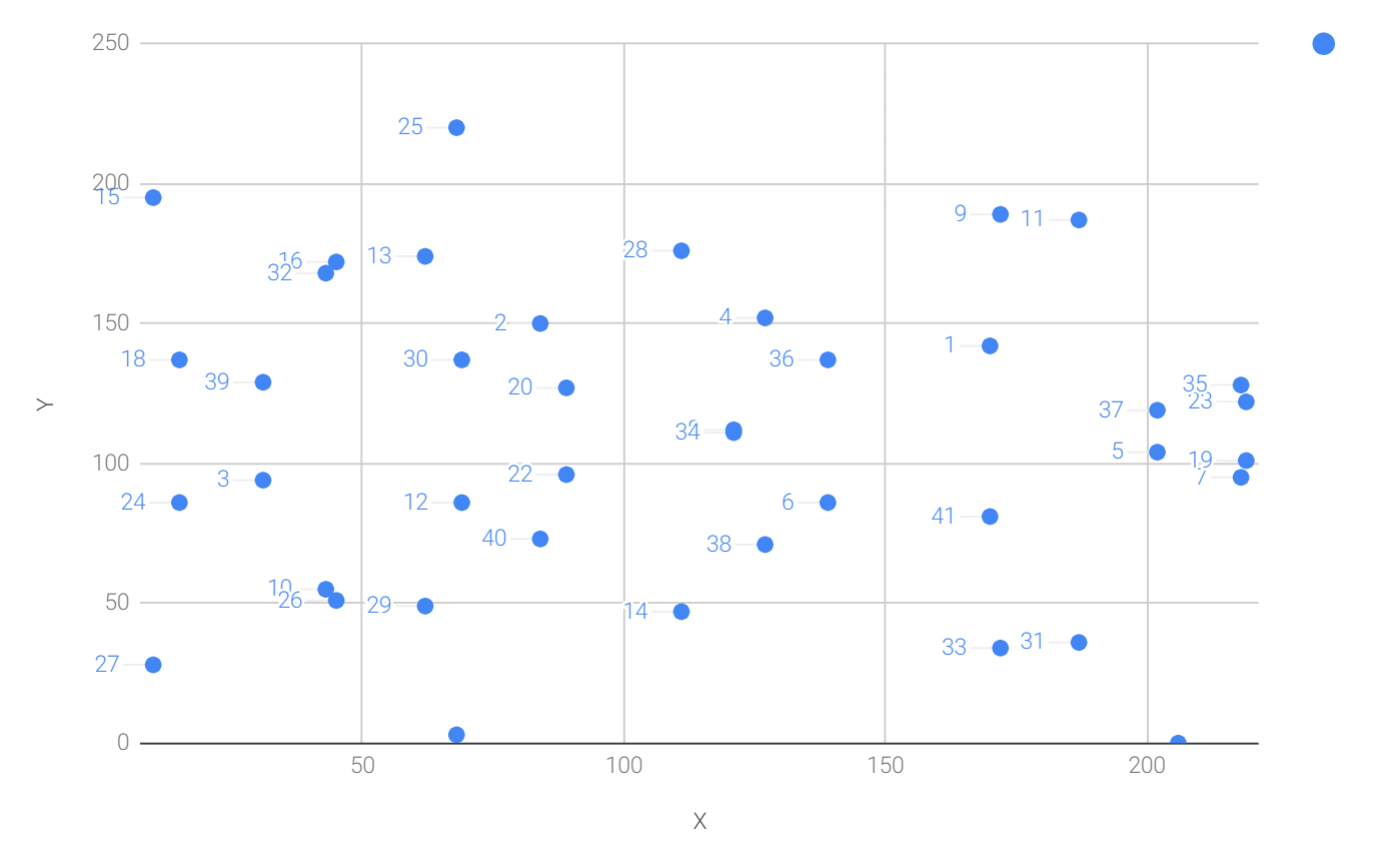
Because we’re evaluating the equation over a Finite Field, the plot of the equation looks vastly different:
As you can see, it’s very much a scattershot of points and there’s no smooth curve here. This is not surprising since the points are discrete. About the only pattern is that the curve is symmetric right around the middle, which is due to the fact that the graph is symmetric, not over the x-axis as in the curve over reals, but about half-way up the y-axis.
What’s important here to realize is that we can evaluate the same equation using the addition, subtraction, multiplication, division and exponentiation as we defined them for Finite Fields and everything still works. This may seem surprising, but abstract math has regularities like this despite being different than the traditional modes of calculation you may be familiar with.
Because we defined an Ellptic curve point and utilize the +,-,* and / operators for Finite Fields, we can actually just combine the two classes to evaluate Elliptic Curve Points over a Finite Field.
>>> from ecc import FieldElement, Point
>>> a = FieldElement(num=0, prime=223)
>>> b = FieldElement(num=7, prime=223)
>>> x = FieldElement(num=192, prime=223)
>>> y = FieldElement(num=105, prime=223)
>>> p1 = Point(x, y, a, b)
>>> print(p1)
Point(192, 105)_223When initializing Point, we will run through this part of the code:
class Point:
def __init__(self, x, y, a, b):
self.a = a
self.b = b
self.x = x
self.y = y
if self.x is None and self.y is None:
return
if self.y**2 != self.x**3 + self.a*self.x + self.b:
raise ValueError('Point ({},{}) is not on the curve'.format(x,y))The addition (+), multiplication (), exponentiation (*) and equality (!=) here will end up utilizing the __add__, __mul__, __pow__ and __ne__ methods from FiniteField respectively and not the integer equivalents. As we will see, being able to do the same equation but with different definitions for the basic arithemtic operators is what will allow us to construct an Elliptic Curve Cryptography library.
We’ve already coded the two classes that we need to implement Elliptic Curve points over a Finite Field. However, to check our work, it will be useful to create a test suite. We will do this using the results of the previous exercise.
from unittest import TestCase
class ECCTest(TestCase):
def test_on_curve(self):
prime = 223
a = FieldElement(0, prime)
b = FieldElement(7, prime)
valid_points = ((192,105), (17,56), (1,193))
invalid_points = ((200,119), (42,99))
# iterate over valid points
for x_raw, y_raw in valid_points:
x = FieldElement(x_raw, prime)
y = FieldElement(y_raw, prime)
# Creating the point should not result in an error
Point(x, y, a, b) # (1)
# iterate over invalid points
for x_raw, y_raw in invalid_points:
x = FieldElement(x_raw, prime)
y = FieldElement(y_raw, prime)
# check that creating the point results in a ValueError
with self.assertRaises(ValueError):
Point(x, y, a, b) # (1)-
We pass in
FieldElementobjects into thePointclass for initialization. This will, in turn, utilize all the overloaded methods inFieldElement
We can now run this test like so:
>>> import ecc
>>> from helper import run_test # (1)
>>> run_test(ecc.ECCTest('test_on_curve'))
.
----------------------------------------------------------------------
Ran 1 test in 0.001s
OK-
helper is a module with some very useful utility functions, including the ability to run unit tests individually.
We can use all the same equations over finite fields, including the linear equation:
y=mx+b
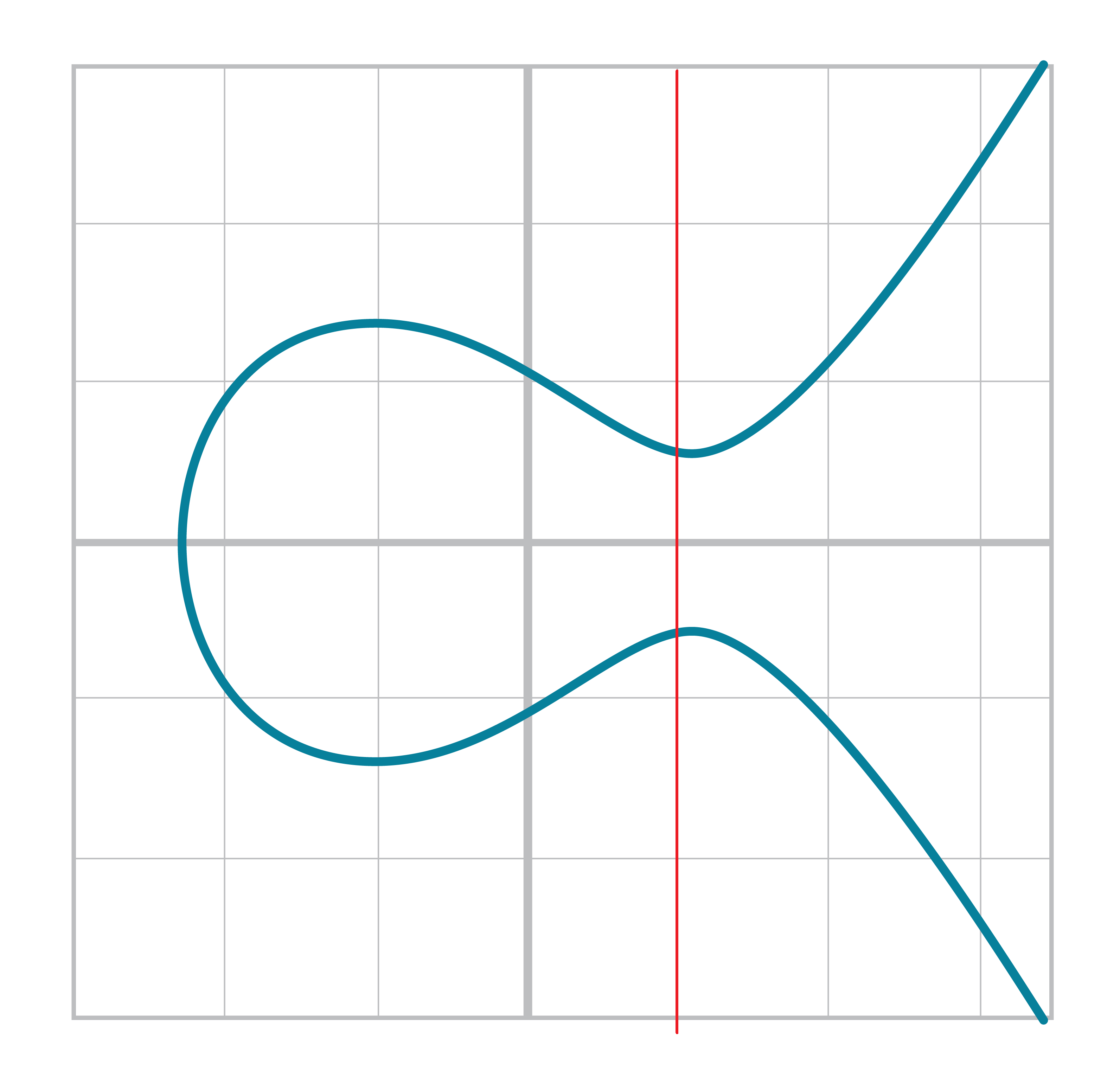
It turns out that a "line" in a finite field is not quite what you’d expect, either:
Still, the equation works and we can calculate what y should be for a given x.
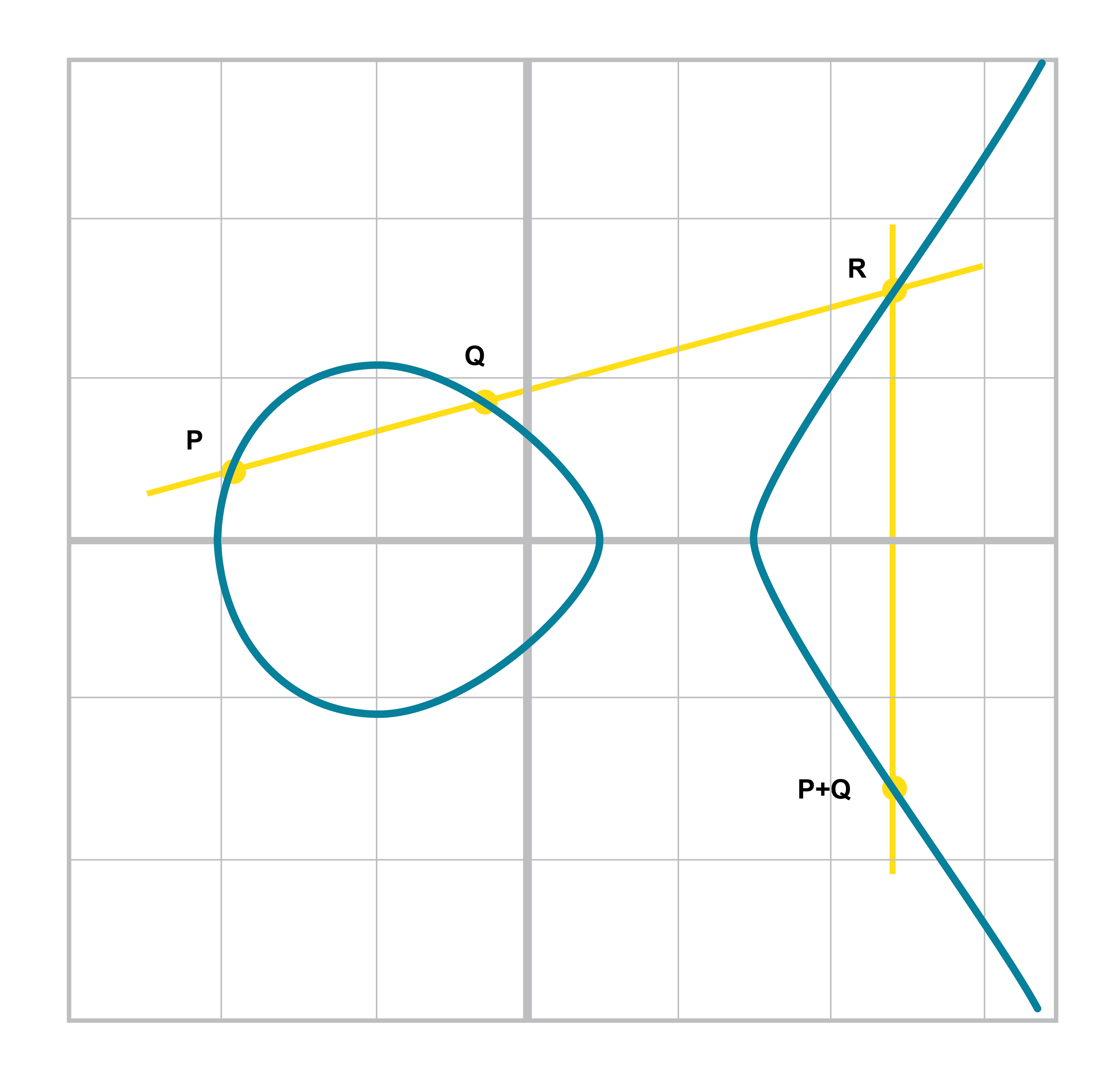
Remarkably, point addition works over finite fields as well. This is because the elliptic curve and line equations still work! The same exact formulas we used to calculate Point Addition over Reals work just as well over Finite Fields. Specifically:
when x1≠x2
P1=(x1,y1), P2=(x2,y2), P3=(x3,y3)
P1+P2=P3
s=(y2-y1)/(x2-x1)
x3=s2-x1-x2
y3=s(x1-x3)-y1
when P1=P2
P1=(x1,y1), P3=(x3,y3)
P1+P1=P3
s=(3x12+a)/(2y1)
x3=s2-2x1
y3=s(x1-x3)-y1
All of the equations for Elliptic Curves work over Finite Fields and that sets us up to create some Cryptographic primitives.
Because we coded FieldElement in such a way as to define __add__, __sub__, __mul__, __truediv__, __pow__, __eq__ and __ne__, we can simply initialize Point with FieldElement objects and point addition will work:
>>> from ecc import FieldElement, Point
>>> prime = 223
>>> a = FieldElement(num=0, prime=prime)
>>> b = FieldElement(num=7, prime=prime)
>>> x1 = FieldElement(num=192, prime=prime)
>>> y1 = FieldElement(num=105, prime=prime)
>>> x1 = FieldElement(num=17, prime=prime)
>>> y1 = FieldElement(num=56, prime=prime)
>>> p1 = Point(x1, y1, a, b)
>>> p2 = Point(x2, y2, a, b)
>>> print(p1+p2)
Point(170,142)_223Because we can add a point to itself, we can introduce some new notation:
(170,142) + (170,142) = 2⋅(170,142)
Similarly, because we have associativity, we can actually add the point again:
2⋅(170,142) + (170,142) = 3⋅(170, 142)
We can actually do this as many times as we want. This is what we call Scalar Multiplication. That is, we have a scalar number in front of the point. We can do this because we have defined point addition.
What’s interesting about scalar multiplication is that it’s really hard to predict without actually calculating:
Each point is labeled by how many times we’ve added the point. You can see that this is a complete scattershot.
This is because point addition is non-linear. That is, not easy to calculate. In fact, doing the scalar multiplication is more or less straightforward, but doing the opposite, Point division, is not.
This is called the Discrete Log problem and is the basis of Elliptic Curve Cryptography.
The interesting thing about Scalar Multiplication is that at a certain number, we get to the point at infinity (remember, point at infinity is the additive identity or 0). If we imagine a point G and scalar multiply until we get the point at infinity, we end up with a set like this:
{ G, 2G, 3G, 4G, … nG }
It turns out that this set is called a Group and because n is finite, we have a Finite Group. Groups are interesting mathematically because they behave a lot like addition:
G+4G=5G or aG+bG=(a+b)G
When we combine the fact that scalar multiplication is easy to go in one direction but hard in the other and the mathematical properties of a Group, we have exactly what we need for Elliptic Curve Cryptography.
You may be wondering why the problem of scalar multiplication is referred to as the discrete log problem.
We called the operation between the points "addition", but we could easily have called it a point "operation". Typically, a new operation that you define in math utilizes the dot operator (⋅). The dot operator is also used for multiplication, and it sometimes helps to think that way:
P1⋅P2=P3
When you do lots of multiplying, that’s the same as exponentiation. Scalar multiplication when we called it "point addition" becomes scalar exponentiation:
P7=Q
The discrete log problem is really the ability to reverse this:
logPQ=7
The log equation on the left is not analytically calculatable. That is, there is no known formula that you can plug in to get the answer generally. This is all a bit confusing, but it’s fair to say that we could call the problem the "Discrete Point Division" problem instead of Discrete Log.
Scalar Multiplication is adding the same point to itself some number of times. The key insight to set up Public Key Cryptography is the fact that scalar multiplication on Elliptic Curves is very hard to reverse. Note the previous exercise. Most likely, you calculated the point s⋅(47,71) in F223 for s from 1 until 21. Here are the results:
>>> from ecc import FieldElement, Point
>>> prime = 223
>>> a = FieldElement(0, prime)
>>> b = FieldElement(7, prime)
>>> x = FieldElement(47, prime)
>>> y = FieldElement(71, prime)
>>> p = Point(x, y, a, b)
>>> for s in range(1,21):
>>> result = s*p
>>> print('{}*(47,71)=({},{})'.format(s,result.x.num,result.y.num))
1*(47,71)=(47,71)
2*(47,71)=(36,111)
3*(47,71)=(15,137)
4*(47,71)=(194,51)
5*(47,71)=(126,96)
6*(47,71)=(139,137)
7*(47,71)=(92,47)
8*(47,71)=(116,55)
9*(47,71)=(69,86)
10*(47,71)=(154,150)
11*(47,71)=(154,73)
12*(47,71)=(69,137)
13*(47,71)=(116,168)
14*(47,71)=(92,176)
15*(47,71)=(139,86)
16*(47,71)=(126,127)
17*(47,71)=(194,172)
18*(47,71)=(15,86)
19*(47,71)=(36,112)
20*(47,71)=(47,152)If we look closely at the numbers, there’s no real discernible pattern to the scalar multiplication. The x-coordinates don’t always increase or decrease and neither do the y-coordinates. About the only pattern in this set is that between 10 and 11, the x coordinates seem to be aligned (10 and 11 have the same x, as do 9 and 12, 8 and 13 and so on).
Scalar Multiplication looks really random and that’s what we’re going to use for what we call an assymetric problem. An assymetric problem is one that’s easy to calculate in one direction, but hard to reverse. For example, it’s easy enough to calculate 12⋅(47,71). But if we were presented this:
s⋅(47,71)=(194,172)
Would you be able to solve for s? We can look up the table above, but that’s because we have a small field. We’ll see later that when we have numbers that are a lot larger, this becomes problematic.
The preceding math (Finite Fields, Elliptic Curves, combining the two), was really to bring us to this point. What we really want to generate for the purposes of Public Key Cryptography are Finite Cyclic Groups and it turns out that if we take a Generator Point from an Elliptic Curve over a Finite Field, we can then generate this Finite Cyclic Group.
Unlike fields, groups have only a single operation. In our case, Point Addition is our operation. We also have a few other properties like closure, invertibility, commutativity and associativity. Lastly, we need the identity.
It turns out that we have all of these things with Point Addition. Let’s look at each property
If you haven’t guessed by now, the identity is defined as the point at infinity. This is the point, when added to any other point produces the other point. So:
0 + P = P
We call 0 the point at infinity because visually, it’s the point that exists to help the math work out:
This is perhaps the easiest to prove since we generated the group in the first place by adding G over and over. Thus, two different elements look like this:
aG + bG
We know that the result is going to be:
(a+b)G
How do we know if this element is in the group? If a+b < n, then we know it’s in the group by definition. If a+b >= n, then we know a < n and b < n, so a+b<2n so a+b-n<n.
(a+b-n)G=aG+bG-nG=aG+bG-O=aG+bG
So we know that this element is in the group, proving closure.
Visually, invertibility is easy to see:
Mathematically, we know that if aG is in the group, (n-a)G is also in the group. You can add them together to get 0.
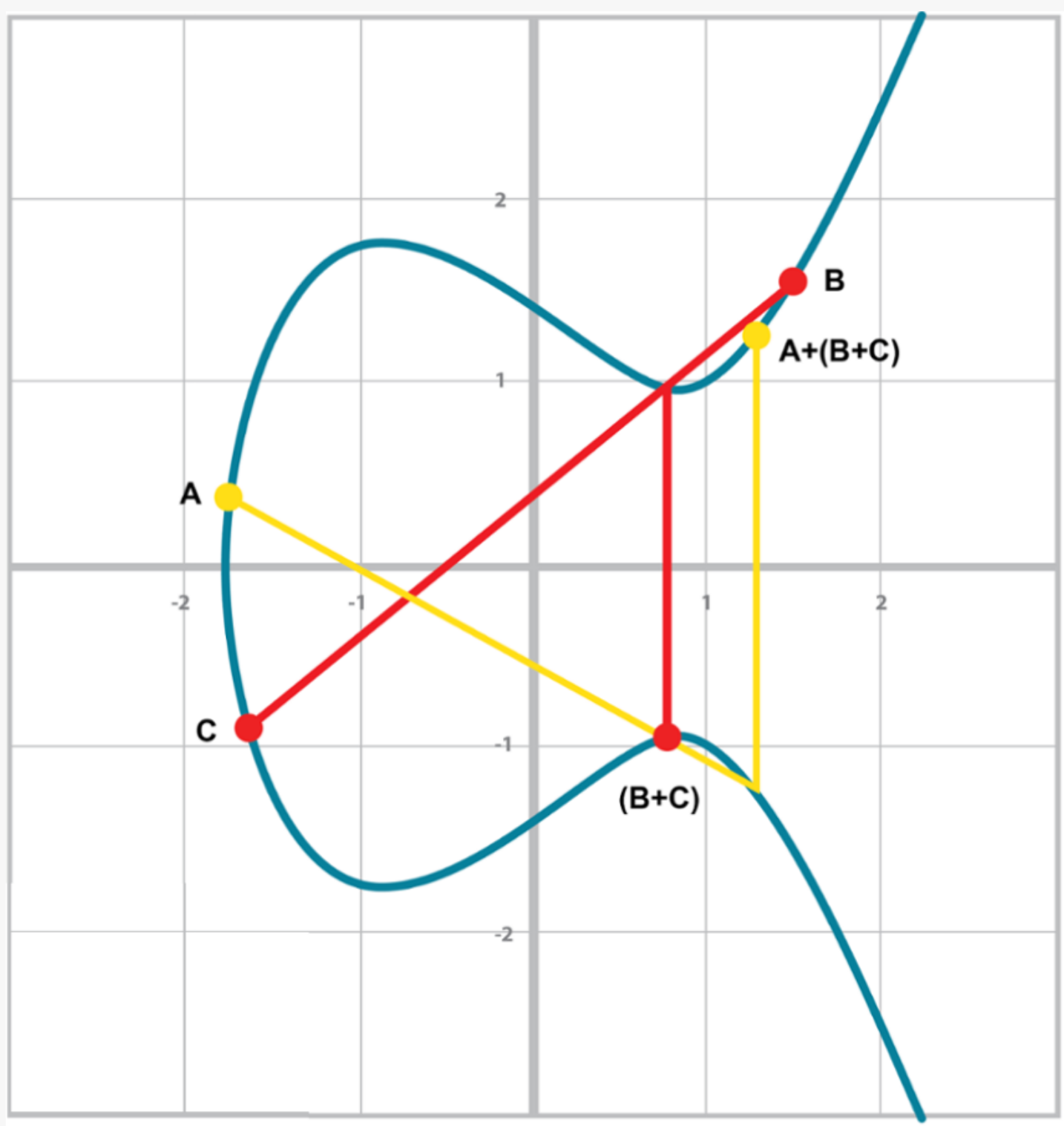
Again, this is very easy to see visually:
Clearly, P+Q=Q+P because they end up drawing the same line.
The equations for figuring out the third point also make this clear:
P1=(x1,y1), P2=(x2,y2), P3=(x3,y3)
x3=s2-x1-x2
y3=s(x1-x3)-y1=s(x2-x3)-y2
You can swap P1 and P2 to get the exact same equation.
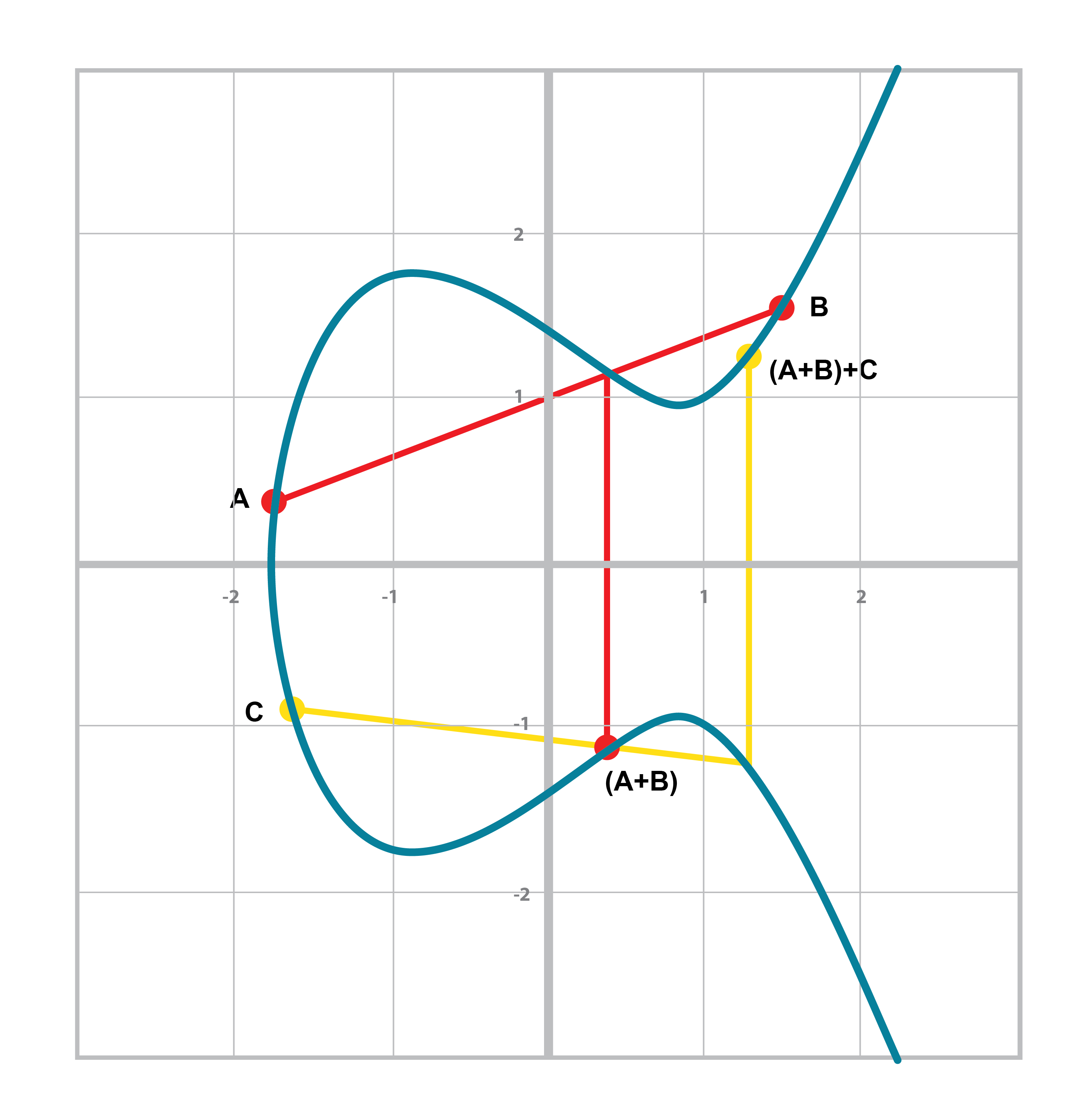
This is the hardest to prove but can be seen visually from the last chapter:
Mathematically, this is a bit more involved, but the math can be proven given the definition that we have. There are proofs of this, but the polynomials involved take several pages and are thus outside the scope of this book.
What we’re trying to do with the last exercise is something like this:
>>> from ecc import FieldElement, Point
>>> prime = 223
>>> a = FieldElement(0, prime)
>>> b = FieldElement(7, prime)
>>> x = FieldElement(15, prime)
>>> y = FieldElement(86, prime)
>>> p = Point(x, y, a, b)
>>> 7*p
Point(infinity)We want to be able to scalar multiply the point with some number. Thankfully, there’s a method in Python called __rmul__ that can be used to override the front multiplication. A naive implementation looks something like this:
class Point:
...
def __rmul__(self, coefficient):
product = self.__class__(None, None, self.a, self.b) # (1)
for _ in range(coefficient): # (2)
product += self
return product-
We start the
productat "zero", which in case of Point Addition is the point at infinity. -
We loop
coefficienttimes and add the point each time
This is fine for small coefficients, but what if we have a very large coefficient? That is, a number that’s so large that we won’t be able to get out of this loop in a reasonable amount of time? If coefficient is 1 trillion, this is going to take a really long time, for example.
It turns out there’s a really fun technique called binary expansion. If bits is the number of bits required to represent the number coefficient, we only have to loop bits times. Note that 1 trillion is still only 40 bits, so we only have to loop 40 times for a number that’s generally considered very large.
import math
class Point:
...
def __rmul__(self, coefficient):
bits = math.ceil(math.log(coefficient, 2))
current = self # (2)
result = Point(None, None, self.a, self.b) # (3)
for _ in range(self.bits): # (4)
if coefficient & 1: # (5)
result += current
current += current # (6)
coefficient >>= 1 # (7)
return result-
We can calculate how many bits a number takes up by doing a log and then taking the ceiling of that number.
-
currentrepresents the point that’s at the current bit. First time through the loop it represents 1*self, the second time, it will be 2*self, third time, 4*self, then 8*self and so on. We double the point each time. In binary the coefficients are 1, 10, 100, 1000, 10000, etc. -
We start the result at "zero", or in Point Addition, the point at infinity.
-
We need to double the point until we’re past how big the coefficient can be.
-
This is a bitwise and, which tells us if the last binary digit is a 1. If so, we add the point corresponding to that bit (1*self, 2*self, 4*self, etc)
-
This is how we double the point.
-
We need to bit shift the coefficient to the right.
This is an advanced technique and if you don’t understand bitwise operators, think of representing the coefficient in binary and only adding the point where there are 1’s.
With __add__ and __rmul__, we can now start defining some more complicated Elliptic Curves.
While we’ve been using relatively small primes for the sake of examples, we are not restricted to such small numbers. Small primes mean that we can use a computer to search through the entire Group. That is try every single point in the group. That is, if the group has a size of 301, the computer can easily do 301 computations to figure out what the scalar multiple was.
But what if we made the prime larger? It turns out that we can choose much larger primes than we’ve been using. Indeed the security of Elliptic Curve Cryptography depends on computers not being able to go through the entire space of the group.
Any Elliptic Curve has to be defined with the following parameters:
-
We have to define a, b of the curve y2=x3+ax+b.
-
We also define the prime of the finte field, p.
-
We define the x and y coordinates of the generator point G
-
We also have the order of the group generated by G, n.
These numbers are known publicly and together form the curve. There are many curves and they have different security/convenience tradeoffs, but the one we’re most interested in is the one defined for Bitcoin. Specifically, the curve secp256k1. The parameters for secp256k1 are thus:
-
a = 0, b = 7, making the equation y2=x3+7
-
p = 2256-232-977
-
G = (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
-
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
The numbers starting with '0x' indicate this is a hexadecimal number.
There are a few things to notice about this curve. First, the equation is relatively simple. Many curves have a and b that are 256 bits long. secp256k1 has a really simple equation.
Second, p is really, really close to 2256. This means that most numbers under 2256 are in the prime field. n is also very close to 2256. This means most points on the curve are in the group. The curve was chosen, in part, because n is so close to P.
Third, 2256 is a really big number (See the sidebar to see just how huge). Amazingly, any number below 2256 can be stored in 32 bytes. This means that we can still store the private key relatively easily.
Lastly, the curve itself is one that was published by Centcom, and is not a NIST curve. NIST stands for xxx and is published by the NSA and Satoshi apparently didn’t trust any curves chosen by the NSA.
2256 doesn’t seem that big because we can express it succinctly, but in reality, it is an enormous number. To give you an idea, here are some relative scales:
2256 ~ 1077
-
Number of atoms in and on earth ~ 1050
-
Number of atoms in the solar system ~ 1057
-
Number of atoms in the Milky Way ~ 1068
-
Number of atoms in the universe ~ 1080
A trillion (109) computers doing a trillion computations every trillionth (10-9) of a second for a trillion years is still only 1056 computations. It’s simply infeasible to brute force a private key.
Think of finding a private key this way. It is a billion times easier to find a particular atom in the Milky Way than to find a private key in Bitcoin.
Since we know all of the parmeters for secp256k1, we can verify in Python whether the generator point, G, is on the curve y2=x3+7:
>>> gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
>>> gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
>>> p = 2**256 - 2**32 - 977
>>> gy**2 % p == (gx**3 + 7) % p
TrueFurthermore, we can verify in Python whether the generator point, G, has the order N.
>>> from ecc import FieldElement, Point
>>> gx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
>>> gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
>>> p = 2**256 - 2**32 - 977
>>> n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
>>> x = FieldElement(gx, p)
>>> y = FieldElement(gy, p)
>>> seven = FieldElement(7, p)
>>> zero = FieldElement(0, p)
>>> G = Point(x, y, zero, seven)
>>> n*G
Point(infinity)Since we know the curve we will work in, this might be a good time to create a subclass in Python to work exclusively with the parameters for secp256k1. We’ll define the equivalent FieldElement and Point objects, but specific to the secp256k1 curve. Let’s start by defining the field we’ll be working in.
P = 2**256 - 2**32 - 977
class S256Field(FieldElement):
def __init__(self, num, prime=None):
super().__init__(num=num, prime=P)
def __repr__(self):
return '{:x}'.format(self.num).zfill(64)We’re really only just subclassing the FieldElement so we don’t have to pass in P all the time. We also want to have a nice way to display a 256-bit number and we do this by using the hexadecimal representation and make sure it fills 64 characters so we can see any leading zeroes.
Similarly, we can define a point on the secp256k1 curve and call it S256Point.
A = 0
B = 7
class S256Point(Point):
zero = S256Field(0) # (1)
def __init__(self, x, y, a=None, b=None):
a, b = S256Field(A), S256Field(B)
if type(x) == int:
super().__init__(x=S256Field(x), y=S256Field(y), a=a, b=b)
else:
super().__init__(x=x, y=y, a=a, b=b) # (2)
def __repr__(self):
if self.x is None:
return 'Point(infinity)'
else:
return 'Point({},{})'.format(self.x, self.y)-
zeroneeds to be defined as aS256Fieldobject so that the equality in the __add__ method still works. -
In case we initialize with the point at infinity, we need to let x and y through directly instead of using the
S256Fieldclass.
This should give us an easier way to initialize a point on the secp256k1 curve, without having to define the a and b every time like we have to with the Point class.
We can also define __rmul__ a bit more efficiently since we know the order of the group, N.
class S256Point(Point):
...
def __rmul__(self, coefficient):
coef = coefficient % N # (1)
current = self
result = S256Point(None, None)
while coef:
if coef & 1:
result += current
current += current
coef >>= 1
return result-
We can mod by N because
N*G==Point(infinity). That is, every N times we add G to itself or any member of this group, we effectively go back to zero (Point at infinity).
We can also define G directly and keep it around since we’ll be using it a lot going forward. We’ll also define N since that’s very useful.
G = S256Point(
0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8,
)
N = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141Now checking that the order of G is N is trivial:
>>> from ecc import G, N
>>> N*G
Point(infinity)We can now describe Public Key Cryptography and how we can use Elliptic Curves over finite fields to build this up. In general, we need a finite cyclical group, which we have with point addition in order to make everything work.
The key here is that when we have P=eG that this is an asymmetric equation. We can easily compute P when we know e and G, but we cannot easily compute s when we know P and G. This is the Discrete Log Problem described earlier.
We’ll use the fact that it’s extremely difficult to compute e to create signing and verification.
Generally, we call e the Private Key and P the Public Key. We’ll note here that the private key is a single 256-bit number and the public key is a coordinate (x,y) where x and y are each 256-bit numbers.
To set up the motivation for why signing and verification exists, imagine this scenario. You want to prove that you are a really good archer, like at the level where you can hit any target you want within 500 yards.
Now if someone could observe you and interact with you, proving this would be easy. Perhaps they would position your son 400 yards away with an apple on his head and challenge you to hit that apple with an arrow. You, being a very good archer do this and prove that you are indeed, a very good archer. The target, if specified by the challenger, is easy for that challenger to verify.
Unfortunately, this doesn’t scale very well. If, for example you wanted to prove this to 10 people, you would have to shoot 10 different arrows at 10 different targets from 10 different challenges. What we want is something that you can do once, requires no interaction but still proves that you are indeed, a good archer.
If, for example, you shot an arrow into a target of your choosing, then the people observing afterwards won’t necessarily be convinced. After all, you may be a sneaky person that paints the target around wherever your arrow happened to land. So what can you do?
Here’s a very clever thing you can do. Forge the tip of the arrow with the name of the target that you’re hitting ("apple on top of my son’s head") and then hit that target with your arrow. Now anyone seeing the target can take an x-ray machine and look at the tip of the embedded arrow and see that the tip indeed says exactly where it was going to hit. The tip clearly had to be forged before the arrow was shot, so this can prove you are indeed a good archer.
This is the same technique we’re using with signing and verification, except what we’re proving isn’t that we’re good archers, but that we know a secret number. We want to prove possession of the secret without revealing the secret itself. We do this by putting the target into our calculation and hitting that target.
Ultimately this is going to be used in Transactions which will prove that the rightful owners of the secrets are spending the Bitcoins and not someone who doesn’t know the secret.
The forging of the target depends on the signature algorithm, and in our case, our signature algorithm is called Elliptic Curve Digital Signature Algorithm, or ECDSA for short.
The secret in our case is e satisfying:
eG = P
Where P is the public key and e is the private key.
The target that we’re going to aim at is more or less random. We are going to choose a random value k which is a 256-bit number. We then do this:
kG = R
R is our target. This is what we’re aiming for. And in fact, we’re only going to care about the x-coordinate of R, which we’ll call r. You may have guessed already that r here stands for random.
We claim at this point that this equation is equivalent to the Discrete Log Problem:
uG+vP=kG where k was chosen randomly and u,v≠0 can be chosen and G,P are known
This is due to the fact that:
uG+vP=kG implies vP=(k-u)G
we know v≠0, so we can divide by the scalar multiple v.
P=((k-u)/v)G
If we can choose k, u and v to solve this equation, then we can solve for e:
eG=((k-u)/v)G implies e = (k-u)/v
This means either we can break the Discrete Log problem or we knew e all along. Since we assume Discrete Log is hard, we can say e is known by the one who came up with u and v.
One subtle thing that we haven’t talked about is that we have to incorporate the purpose of our shooting. This is a contract that gets fulfilled as a result of the shooting at the target. William Tell, for example, was shooting so that he could save his son (shoot the target and you get to save your son). You can imagine there would be other reasons to hit the target and the "reward" that the person hitting the target would receive. This has to be incorporated into our equations.
In signature/verification parlance, this is called the signature hash. This generally is the hash of the message that both parties agree to that reveal the intent of the shooter. We denote this with the letter z. This is incorporated into our uG+vP calculation this way:
u = r/s, v = z/s
Since r is used in the calculation of u, we now have the tip of the arrow forged. We also have the intent of the shooter incorporated into v, so both the reason for shooting and the target that is being aimed at are now a part of the equation.
To make the equation work, we can calculate s:
uG+vP=R=kG
uG+veG=kG
u+ve=k
r/s+ze/s=k
(r+ze)/s=k
s=(r+ze)/k
This is indeed the basis of the signature algorithm and the two numbers actually communicated as part of the signature are r and s.
Verification is simple:
uG+vP where u,v≠0
uG+vP=(r/s)G+(ze/s)G=r+ze)/s)G=((r+ze)/((r+ze)/kG=kG=(r,y)
kAt this point, you might be wondering why we don’t reveal k and instead reveal the x-coordinate of R or r. If we were to reveal k, then:
uG+vP=R
uG+veG=kG
kG-uG=veG
(k-u)G = veG
(k-u) = ve
(k-u)*1/v = e
Means that we’ll be revealing our secret, which would defeat the whole purpose of the signature. We can, however, reveal R.
Generally, signatures sign some fixed-length value (our "contract"), in our case something that’s 32 bytes. The fact that 32 bytes is 256 bits is not a coincidence as the thing we’re signing needs to be a scalar for G.
In order to guarantee that thing we’re signing is 32 bytes, we hash the document first. In Bitcoin, the hashing function is double-sha256. This guarantees the thing that we’re signing is exactly 32 bytes. We will call the result of the hash, z.
The actual signature that we are verifying has two components, (r, s). The r is as above, it’s the x-coordinate of some point R that we’ll come back to. s is going to be defined as this:
s = (z+re)/k
Keep in mind that we know e (eG = P, or what we’re proving we know in the first place), we know k (kG = R, remember?) and we know z.
We will now construct R=uG+vP by defining u and v this way:
u = z/s v = r/s
Thus:
uG + vP = (z/s)G + (r/s)P = (z/s)G + (re/s)G = ((z+re)/s)G
We know s = (z+re)/k so:
uG + vP = z+re)/((z+re)/kG = kG = R
We’ve successfully chosen u and v in a way as to generate R as we intended. Furthermore, we used r in the calculation of v proving we knew what R should be. The only way we could know the details of R beforehand is if we know e, proving we know e.
To whit, here are the steps:
-
We are given (r, s) as the signature, z as the hash of the thing being signed and P, the public key (or public point) of the signer.
-
We calculate u = z/s, v = r/s
-
We calculate uG + vP = R
-
If R’s x coordinate equals r, the signature is valid.
The calculation of z requires two rounds of sha256. You may be wondering why there are two rounds when only 1 is necessary to get a 256-bit number. The reason is for security.
There is a well-known hash collision attack on SHA1 called a birthday attack which basically makes finding collisions much easier. This is how Google found a SHA1 collision in 2017. Using SHA1 twice, or double-SHA1 is the way to defeat this attack.
There is no known SHA2 (of which SHA256 is a part) birthday attack, but is doubled in case one is found.
We can now verify a signature using some of the primitives that we have.
>>> from ecc import S256Point, G, N
>>> z = 0xbc62d4b80d9e36da29c16c5d4d9f11731f36052c72401a76c23c0fb5a9b74423
>>> r = 0x37206a0610995c58074999cb9767b87af4c4978db68c06e8e6e81d282047a7c6
>>> s = 0x8ca63759c1157ebeaec0d03cecca119fc9a75bf8e6d0fa65c841c8e2738cdaec
>>> point = S256Point(0x04519fac3d910ca7e7138f7013706f619fa8f033e6ec6e09370ea38cee6a7574, 0x82b51eab8c27c66e26c858a079bcdf4f1ada34cec420cafc7eac1a42216fb6c4)
>>> u = z * pow(s, N-2, N) % N # (1)
>>> v = r * pow(s, N-2, N) % N # (2)
>>> print((u*G + v*point).x.num == r) # (3)
True-
u = z/s. Note that we use Fermat’s Little Theorem for 1/s, since N is prime.
-
v = v/s. Note that we use Fermat’s Little Theorem for 1/s, since N is prime.
-
uG+vP = (r,y). We need to check that the x-coordinate is r)
Verify whether these signatures are valid:
P = (0x887387e452b8eacc4acfde10d9aaf7f6d9a0f975aabb10d006e4da568744d06c,
0x61de6d95231cd89026e286df3b6ae4a894a3378e393e93a0f45b666329a0ae34)
# signature 1
z, r, s = 0xec208baa0fc1c19f708a9ca96fdeff3ac3f230bb4a7ba4aede4942ad003c0f60,
0xac8d1c87e51d0d441be8b3dd5b05c8795b48875dffe00b7ffcfac23010d3a395,
0x68342ceff8935ededd102dd876ffd6ba72d6a427a3edb13d26eb0781cb423c4
# signature 2
z, r, s = 0x7c076ff316692a3d7eb3c3bb0f8b1488cf72e1afcd929e29307032997a838a3d,
0xeff69ef2b1bd93a66ed5219add4fb51e11a840f404876325a1e8ffe0529a2c,
0xc7207fee197d27c618aea621406f6bf5ef6fca38681d82b2f06fddbdce6feab6We already have a class S256Point which is the publc point for the private key. For a variety of reasons, we’re going to create a Signature class that houses the r and s values:
class Signature:
def __init__(self, r, s):
self.r = r
self.s = sWe will be doing more with this class later.
We can create an actual verify method on S256Point based on the above.
class S256Point(Point):
...
def verify(self, z, sig):
s_inv = pow(sig.s, N-2, N) # (1)
u = z * s_inv % N # (2)
v = sig.r * s_inv % N # (3)
total = u*G + v*self # (4)
return total.x.num == sig.r (5)-
s_inv (1/s) is calculated using Fermat’s Little Theorem on the order of the group
Nwhich is prime. -
u = z/s. Note that we can mod by N as that’s the order of the group.
-
v = r/s. Note that we can mod by N as that’s the order of the group.
-
uG+vP should be R
-
We check that the x-coordinate is r
So given a public key (or point on the elliptic curve), we can verify whether a signature is valid or not.
Given that we know how verification should work, signing is more or less straightforward. The only missing step is figuring out what k, and thus R=kG to use.
It turns out that we can choose k at random and everything still works. We do this by choosing a random k.
Signing Procedure:
-
We are given z. We know e and eG=P.
-
Choose a random k
-
Calculate R=kG and r=x-coordinate of R
-
Calculate s = (z+re)/k
-
Signature is (r,s)
Note that the pubkey P and z have to be transmitted to whoever wants to verify as well. We’ll see later that z is computed and P is sent along with the signature.
We can now create a signature using some of the primitives that we have.
>>> from ecc import S256Point, G, N
>>> from random import randint
>>> from helper import double_sha256
>>> e = int.from_bytes(double_sha256(b'my secret'), 'big') # (1)
>>> z = int.from_bytes(double_sha256(b'my message'), 'big') # (2)
>>> k = randint(0, N)
>>> r = (k*G).x.num # (3)
>>> k_inv = pow(k, N-2, N)
>>> s = (z+r*e) * k_inv % N # (4)
>>> point = e*G # (5)
>>> print(point)
S256Point(028d003eab2e428d11983f3e97c3fa0addf3b42740df0d211795ffb3be2f6c52,0ae987b9ec6ea159c78cb2a937ed89096fb218d9e7594f02b547526d8cd309e2)
>>> print(hex(z))
0x231c6f3d980a6b0fb7152f85cee7eb52bf92433d9919b9c5218cb08e79cce78
>>> print(hex(r))
0x3b5847f623a77be3be544c00b8abb83540ad44c691a1e0df7f60fcedd912d311
>>> print(hex(s))
0x40dbad2b4e539ffe797a6f41d414de5e38c5bd09aafe54b87a6dffe68c60f224-
This would be something like a "brain wallet". Please don’t use this for a real secret.
-
This is the message that we’re signing.
-
kG = (r,y) so we take the x coordinate only
-
s = (z+re)/k. We mod by N because we know this is a cyclical group of order N
-
The public point needs to be known by the verifier
Sign the following message with the secret
e = 12345
z = int.from_bytes(double_sha256('Programming Bitcoin!'), 'big')In order to program message signing, we first need to create a PrivateKey class which will house our secret/scalar/private key.
class PrivateKey:
def __init__(self, secret):
self.secret = secret
self.point = secret*GWe keep around the public key (self.point) for convenience. We can now create the sign method.
from random import randint
...
# class PrivateKey
def sign(self, z):
k = randint(0, N) # (1)
r = (k*G).x.num # (2)
k_inv = pow(k, N-2, N) # (3)
s = (z + r*self.secret) * k_inv % N # (4)
if s > N/2: # (5)
s = N - s
return Signature(r, s) # (6)-
randint chooses a random integer from (0,N).
-
r is the x-coordinate of kG
-
We use Fermat’s Little Theorem again and N, which is prime
-
s = (z+re)/k
-
It turns out that we have to use a low-s value for malleability reasons
-
We return a Signature object from above.
The s here has to be a low value
There’s an important rule in signatures that utilize a random component like we have here. The k needs to be random. That is, it cannot get reused. In fact, a k that’s reused will result in you losing your secret! This is because:
Our secret is e and our z is the same.
k1G=(r1,y), k2G=(r2,y) s1 = (z+r1e), s2 = (z+r2e)
s1-s2 = (r1-r2)e e = (s1-s2) / (r1-r2)
If anyone sees both signatures, they can run this formula and find our secret!
To combat this, there is a deterministic k generation standard which uses our secret and z to create a unique k every time. The specification is laid out in RFC6979 and the code looks like this:
class PrivateKey:
...
def deterministic_k(self, z):
k = b'\x00' * 32
v = b'\x01' * 32
if z > N:
z -= N
z_bytes = z.to_bytes(32, 'big')
secret_bytes = self.secret.to_bytes(32, 'big')
s256 = hashlib.sha256
k = hmac.new(k, v + b'\x00' + secret_bytes + z_bytes, s256).digest()
v = hmac.new(k, v, s256).digest()
k = hmac.new(k, v + b'\x01' + secret_bytes + z_bytes, s256).digest()
v = hmac.new(k, v, s256).digest()
while 1:
v = hmac.new(k, v, s256).digest()
candidate = int.from_bytes(v, 'big')
if candidate >= 1 and candidate < N:
return candidate # (1)
k = hmac.new(k, v + b'\x00', s256).digest()
v = hmac.new(k, v, s256).digest()-
This algorithm’returns a candidate that’s suitable.
The nice thing about this algorithm is that the k is with very high probability not going to be utilized again. This is because SHA256 is collision-resistant and no collisions to date have been found.
We’ve covered Elliptic Curve Cryptography and we can now prove that we know a secret by signing something and we can also verify that the person with the secret actually signed a message. We now turn to serializing a lot of these structures so that we can store them on disk, send them over the network and so on.