Skip to content

Latest commit

 

History

History
454 lines (337 loc) · 19.9 KB

ch04.asciidoc

File metadata and controls

454 lines (337 loc) · 19.9 KB
Raw

Serialization

We’ve created a lot of classes thus far, including PrivateKey, S256Point, and Signature. We now need to start thinking about how to transmit these objects to other computers on the network, or even to disk. This is where serialization comes into play. We want to communicate or store a S256Point or a Signature or a PrivateKey. Ideally, we want to do this efficiently, for reasons we’ll see in [chapter_networking] (Networking).

Uncompressed SEC format

We’ll start with the S256Point class, which is the public key class. Recall that the public key in Elliptic Curve Cryptography is really a coordinate in the form of (x,y). How can we serialize this data?

It turns out there’s already a standard for serializing ECDSA public keys called SEC. SEC stands for Standards for Efficient Cryptography, and as the word "Efficient" in the name suggests, it’s got minimal overhead. There are two forms of SEC format that we need to be concerned with: uncompressed SEC format and the compressed SEC format.

Here is how the uncompressed SEC format for a given point P = (x,y) is generated:

  1. Start with the prefix byte, which is 0x04.

  2. Next, append the x coordinate in 32 bytes as a Big-Endian integer.

  3. Next, append the y coordinate in 32 bytes as a Big-Endian integer.

The uncompressed SEC format is in Uncompressed SEC Format:

Uncompressed SEC Format
Figure 1. Uncompressed SEC Format
Warning
Big- and Little-Endian

The motivation for Big- and Little-Endian encodings is storing a number on disk. A number under 256 is easy enough to encode, as a single byte (28) is enough to hold it. When it’s bigger than 256, how do we serialize the number to bytes?

Arabic numerals are read left to right. A number like 123 is 100 + 20 + 3 and not 1 + 20 + 300. This is what we call Big-Endian because the Big End starts first.

Computers can sometimes be more efficient using the opposite order, or Little-Endian—that is, starting with the Little End first.

Since computers work in bytes, which have 8 bits, we have to think in base 256. This means that a number like 500 looks like 01f4 in Big-Endian. That is, 500 = 1 × 256 + 244 (f4 in hexadecimal). The same number looks like f401 in Little-Endian.

Unfortunately, some serializations in Bitcoin (like the SEC-format x and y coordinates) are Big-Endian. Other serializations in Bitcoin (like the transaction version number in [chapter_tx_parsing]) are in Little-Endian. This book will let you know which ones are Big- versus Little-Endian.

Creating the uncompressed SEC format serialization is pretty straightforward. The trickiest part being converting a 256-bit number into 32 bytes, Big-Endian. Here’s how this is done in code:

class S256Point(Point):
...
    def sec(self):
        '''returns the binary version of the sec format'''
	return b'\x04' + self.x.num.to_bytes(32, 'big') \
            + self.y.num.to_bytes(32, 'big')  # (1)

  1. In Python 3, you can convert a number to bytes using the to_bytes method. The first argument is how many bytes it should take up and the second argument is the endianness (see Big and Little Endian).

Compressed SEC Format

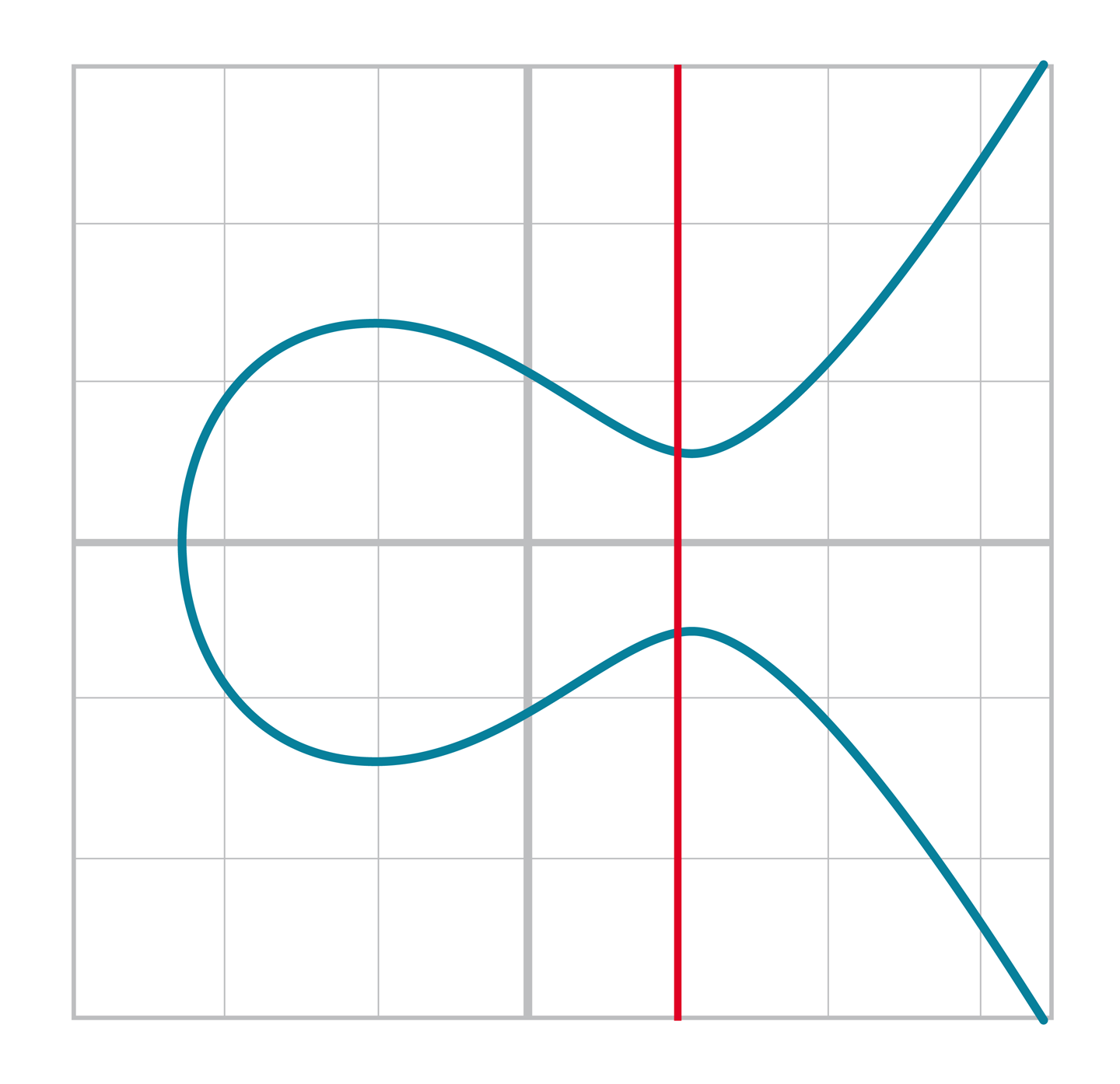
Recall that for any x coordinate, there are at most two y coordinates due to the y2 term in the elliptic curve equation (The two possible values for y are where this vertical line intersects the curve):

Elliptic Curve Vertical Line
Figure 2. The two possible values for y are where this vertical line intersects the curve

It turns out that even over a Finite Field, we have the same symmetry.

This is because for any (x,y) that satisfies y2 = x3 + ax + b, (x,–y) also satisfies the equation. Furthermore, in a Finite Field, –y (mod p) = p – y. Or more accurately, if (x,y) satisfies the elliptic curve equation, (x,p – y) also satisfies the equation. These are the only two solutions for a given x as shown above, so if we know x, we know y coordinate has to be either y or p-y.

Since p is a prime number greater than 2, we know that p is odd. Thus, if y is even, p-y (odd minus even) will be odd. If y is odd, p-y will be even. In other words, between y and p-y exactly one will be even and one will be odd. This is something we can use to our advantage to shorten the Uncompressed SEC Format. We can provide the x coordinate and the even-ness of the y coordinate. We call this the Compressed SEC format because of how the y coordinate is compressed into a single byte (namely, whether it’s even or odd).

Here is the serialization of the Compressed SEC format for a given point P=(x,y):

  1. Start with the prefix byte. If y is even, it’s 0x02, otherwise it’s 0x03.

  2. Next, append the x coordinate in 32 bytes as a Big-Endian integer.

The Compressed SEC format is in Compressed SEC format:

Compressed SEC format
Figure 3. Compressed SEC format

Again, the procedure is pretty straightforward. We can update the sec method to handle compressed SEC keys.

class S256Point(Point):
...
link:code-ch04/ecc.py[role=include]

The big advantage of the Compressed SEC format is that it only takes up 33 bytes instead of 65 bytes. This is a big savings when amortized over millions of transactions.

At this point, you may be wondering how you can analytically calculate y given the x coordinate. This requires us to calculate a square root in a Finite Field.

Stated mathematically:

Find w such that w2 = v when we know v.

It turns out that if the Finite Field prime p % 4 = 3, we can do this rather easily. Here’s how.

First, we know:

  • p % 4 == 3

which implies

  • (p + 1) % 4 == 0

That is, (p + 1)/4 is an integer.

By definition,

  • w2 = v

We are looking for a formula to calculate w. From Fermat’s Little Theorem:

  • wp–1 % p = 1

which means:

  • w2=w2 ⋅ 1 = w2 ⋅ wp–1=w(p+1)

Since p is odd (recall p is prime), we know we can divide (p+1) by 2 and still get an integer implying

  • w = w(p+1)/2

Now we can use (p+1)/4 being an integer this way:

  • w = w(p+1)/2 = w2(p+1)/4 = (w2)(p+1)/4 = v(p+1)/4

So our formula for finding the square root becomes:

  • if w2 = v and p % 4 = 3, w = v(p+1)/4

It turns out that the p used in secp256k1 is such that p % 4 == 3, so we can use this formula:

  • w2 = v

  • w = v(p+1)/4

That will be one of the two possible w's; the other will be p – w. This is due to taking the square root means that both the positive and negative will work.

We can add this as a general method in the S256Field:

class S256Field(FieldElement):
...
link:code-ch04/ecc.py[role=include]

When we get a serialized SEC pubkey, we can write a parse method to figure out which y we need:

class S256Point:
...
link:code-ch04/ecc.py[role=include]

  1. The uncompressed is pretty straightforward.

  2. The evenness of the y coordinate is given in the first byte.

  3. We take the square root of the right side of the Elliptic Curve equation to get the y.

  4. Determine evenness and return the correct point.

DER Signatures

Another class that we need to learn to serialize is Signature. Much like the SEC format, it needs to encode two different numbers, r and s. Unfortunately, unlike S256Point, Signature cannot be compressed as s cannot be derived solely from r.

The standard for serializing signatures (and lots of other things, for that matter) is called DER format. DER stands for Distinguished Encoding Rules and was used by Satoshi to serialize signatures. This was most likely because the standard was already defined in 2008, supported in the OpenSSL library (used in Bitcoin at the time), and was easy enough to adopt, rather than creating a new standard.

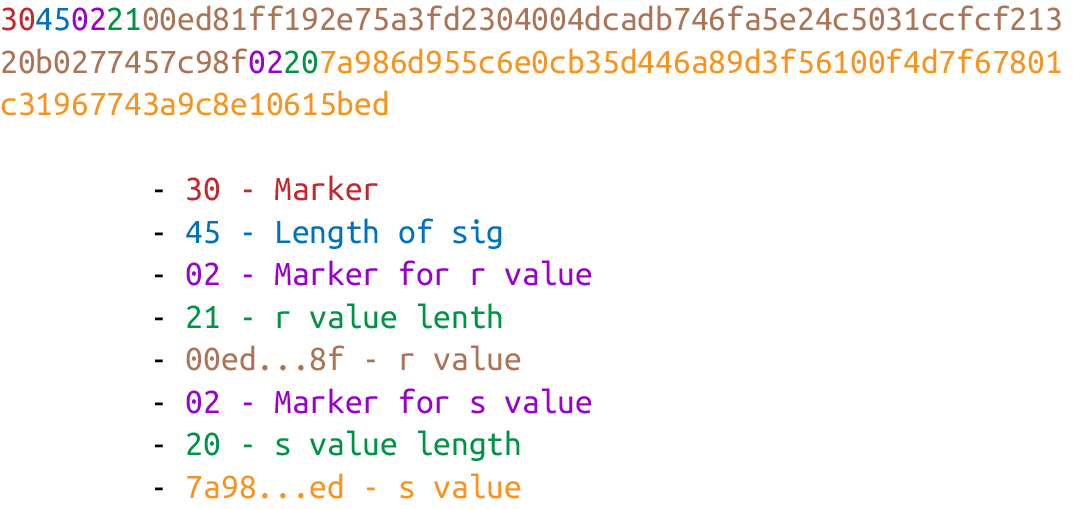
DER Signature format is defined like this:

  1. Start with the 0x30 byte.

  2. Encode the length of the rest of the signature (usually 0x44 or 0x45) and append.

  3. Append the marker byte 0x02.

  4. Encode r as a Big-Endian integer, but prepend with 0x00 byte if r’s first byte ≥ `0x80. Prepend the resulting length to r. Add this to the result.

  5. Append the marker byte 0x02.

  6. Encode s as a Big-Endian integer, but prepend with 0x00 byte if s’s first byte ≥ `0x80. Prepend the resulting length to s. Add this to the result.

The rules for #4 and #6 with the first byte starting with something greater than or equal to 0x80 is because DER is a general encoding and allows for negative numbers to be encoded. The first bit being 1 means that the number is negative. All numbers in an ECDSA signature are positive, so we have to prepend with 0x00 if the first bit is zero which is equivalent to first byte ≥ 0x80.

The DER format is shown in DER format.

DER format
Figure 4. DER format

Because we know r is a 256-bit integer, r will be at most 32 bytes expressed as Big-Endian. It’s also possible the first byte could be ≥ 0x80, so part 4 can be at most 33 bytes. However, if r is a relatively small number, it could be less than 32 bytes. Same goes for s and part 6.

Here’s how this is coded in Python:

class Signature:
...
link:code-ch04/ecc.py[role=include]

  1. In Python 3, you can convert a list of numbers to the byte equivalents using bytes([some_integer1, some_integer2])

Overall, this is an inefficient way to encode r and s as there are at least 4 bytes that aren’t strictly necessary.

Base58

In the early days of Bitcoin, Bitcoins were assigned to public keys specified in SEC format (uncompressed) and then were redeemed using DER signatures. For reasons we’ll get to in [chapter_script], using this particular very simple script turned out to be both wasteful for storing UTXOs and a little less secure than the scripts in more prominent use now. For now, we’ll go through what addresses are and how they are encoded.

Transmitting Your Public Key

In order for Alice to pay Bob, she has to know where to send the money. This is true not just in Bitcoin, but any method of payment. Since Bitcoin is a digital bearer instrument, the address can be something like a public key in a public key cryptography scheme. Unfortunately, SEC format, especially uncompressed is a bit long (65 or 33 bytes). Furthermore, the 65 or 33 bytes are in binary format, not something that’s easy to read, at least raw.

There are three major considerations. The first is that the public key be readable (easy to hand-write and not too difficult to mistake, say, over the phone). The second is that it’s short (not be so long that it’s cumbersome). The third is that it’s secure (harder to make mistakes).

So how do we get readability, compression, and security? If we express the SEC format in hexadecimal (4 bits per character), it’s double the length (130 or 66 characters). Can we do better?

We can use something like Base64, which can express 6 bits per character and becomes 87 characters for uncompressed SEC and 44 characters for compressed SEC. Unfortunately, Base64 is prone to mistakes, as a lot of letters and numbers look similar (0 and O, l and I, - and _). If we remove these characters, we can have something that’s got good readability and decent compression (around 5.86 bits per character). Lastly, we can add a checksum at the end to ensure that mistakes are easy to detect.

This construction is called Base58. Instead of hexadecimal (base 16) or Base64, we’re encoding numbers in Base58.

The actual mechanics of doing the Base58 encoding are as follows.

All numbers, uppercase letters, and lowercase letters are utilized except for the aforementioned 0/O and l/I. That leaves us with 10 + 26 + 26 – 4 = 58. Each of these characters represents a digit in base 58. We can encode with a function that does exactly this:

link:code-ch04/helper.py[role=include]
...
link:code-ch04/helper.py[role=include]

  1. The purpose of this loop is to determine how many of the bytes at the front are 0 bytes. We want to add them back at the end.

  2. This is the loop that figures out what Base58 digit to use.

  3. Finally, we prepend all the zeros that we counted at the front because otherwise, they wouldn’t show up as prefixed ones. This annoyingly happens with pay-to-pubkey-hash (p2pkh). More on that in [chapter_script].

This function will take any bytes in Python 3 and convert it to Base58.

Note
Why Base58 Is on the Way Out

Base58 has been used for a long time, and while it does make it somewhat easier than something like Base64 to communicate, it’s not really that convenient. Most people prefer to copy and paste the addresses, and if you’ve ever tried to communicate a Base58 address over voice, you know it can be a nightmare.

What’s much better is the new Bech32 standard, which is defined in BIP0173. Bech32 uses a 32-character alphabet that’s just numbers and lowercase letters except 1, b, i and o. These are thus far only used for Segwit ([chapter_segwit]).

Address Format

The 264 bits from a compressed SEC format are still a bit too long, not to mention a bit less secure (see [chapter_script]). To both shorten and increase security, we can use the ripemd160 hash to reduce the size to a 20-byte hash.

By not using the SEC format directly, we can go from 33 bytes to 20 bytes, shortening the address significantly. Here is how a Bitcoin address is created:

  1. For mainnet addresses, start with the prefix 0x00, for testnet 0x6f.

  2. Take the SEC format (compressed or uncompressed) and do a sha256 operation followed by the ripemd160 hash operation, the combination which is called a hash160 operation.

  3. Combine the prefix from #1 and resulting hash from #2.

  4. Do a hash256 of the result from #3 and get the first 4 bytes.

  5. Take the combination of #3 and #4 and encode in Base58.

Step 4 of this process is called the checksum. We can do steps 4 and 5 in one go this way:

link:code-ch04/helper.py[role=include]
Note
What Is Testnet?

Testnet is a parallel bitcoin network that’s meant to be used by developers. The coins on there are not worth anything and the proof-of-work required to find a block is relatively easy. The mainnet chain as of this writing has around 550,000 blocks, while testnet has significantly more (around 1,450,000 blocks).

The process of doing a sha256 operation followed by a ripemd160 operation is called a hash160 operation in Bitcoin. We can implement this in helper.py.

link:code-ch04/helper.py[role=include]

  1. Note that hashlib.sha256(s).digest() does the sha256 and the wrapper around it does the ripemd160.

We can also update S256Point to with hash160 and address methods.

class S256Point:
...
link:code-ch04/ecc.py[role=include]

WIF Format

The private key in our case is a 256-bit number. Generally, we are not going to need to serialize our secret that often, as it doesn’t get broadcast (that would be a bad idea!). That said, there are instances where we may want to transfer your private key from one wallet to another, for example, from a paper wallet to a software wallet.

For this purpose, there is a format called WIF, which stands for Wallet Import Format. WIF is a serialization of the private key that’s meant to be human readable. WIF uses the same Base58 encoding that addresses use.

Here is how the WIF format is created:

  1. For mainnet private keys, start with the prefix 0x80, for testnet 0xef.

  2. Encode the secret in 32-byte Big-Endian.

  3. If the SEC format used for the public key address was compressed, add a suffix of 0x01.

  4. Combine the prefix from #1, serialized secret from #2, and suffix from #3.

  5. Do a hash256 of the result from #4 and get the first 4 bytes.

  6. Take the combination of #4 and #5 and encode in Base58.

We can now create the wif method on the PrivateKey class.

class PrivateKey
...
link:code-ch04/ecc.py[role=include]

Big- and Little-Endian Redux

It will be very useful to know how Big- and Little-Endian are done in Python, as the next few chapters will be parsing and serializing numbers to and from Big-/Little-Endian quite a bit. In particular, Satoshi used a lot of Little-Endian for Bitcoin and unfortunately, there’s no easy-to-learn rule for where Little-Endian is used and where Big-Endian is used. Recall that SEC format uses Big-Endian encoding as do addresses and WIF. From [chapter_tx_parsing] onward, we will use Little-Endian encoding a lot more. For this reason, we turn to the next two exercises. The last exercise of this section is to create a testnet address for yourself.

Go to a testnet faucet (https://faucet.programmingbitcoin.com) and send some testnet coins to that address (it should start with m or n or else something is wrong). If you succeeded, congrats! You’re now the proud owner of some testnet coins!

Conclusion

In this chapter we learned how to serialize a lot of different structures that we created in the previous chapters. We now turn to Transactions that we can parse and understand.