📢 This app is now released and deployed at: https://saeed-option-pricing.streamlit.app/
🚀 I am excited to share my project focusing on pricing options. I implemented the Black-Scholes model, Monte Carlo simulations, and the Binomial Tree method for pricing options. I am further developing the project by adding backtesting, a machine learning model, and deploying the app.
👨🏻💻 About me: I believe in hands-on learning. As a Senior Data Scientist with a PhD in Computational Physics, I have a strong foundation in analytical thinking and complex problem-solving. Through hands-on work in finance, I am leveraging my data science skills to gain practical experience and build a robust understanding of financial systems.
Contact my LinkedIn 👨🏻💻
In this project, Black-Scholes model, Monte Carlo simulations, and the Binomial Tree method are vital tools in financial markets for pricing options. Each method offers a distinct approach to estimating the price of call and put options, relying on parameters such as stock price, strike price, time to maturity, risk-free rate, and volatility. I conducted backtesting using Apple Inc. (AAPL) stock data from the year 2013, sourced from https://optiondata.org/. Real-world stock data is fetched via the Yahoo Finance API to compute option prices, historical volatility, and option sensitivities (the Greeks). The project also provides visualisations and comparisons of option prices using all three methods.
- Fetches real-time stock data (e.g., Apple stock) using
yfinance. - Computes option prices for call and put options using:
- Black-Scholes
- Monte Carlo
- Binomial Tree
- Backtesting
- Calculates historical volatility based on daily returns.
- Computes the Greeks: Delta, Gamma, Vega, Theta, and Rho.
- Calculates Implied Volatility based on market prices.
- Provides visualisations showing how option prices vary with stock price for both calls and puts.
- Compares pricing results from the three methods.
- Stock Ticker
- Stock Price (S)
- Strike Price (K)
- Days to Expiration
- Risk-Free Rate (r)
- Market Price of the Option
The script will generate the following output:
-
options_report.txt: a report file containing:
- Call and Put Option Prices using Black-Scholes, Monte Carlo, and Binomial Tree methods.
- Greeks and implied volatility.
-
Plots containing:
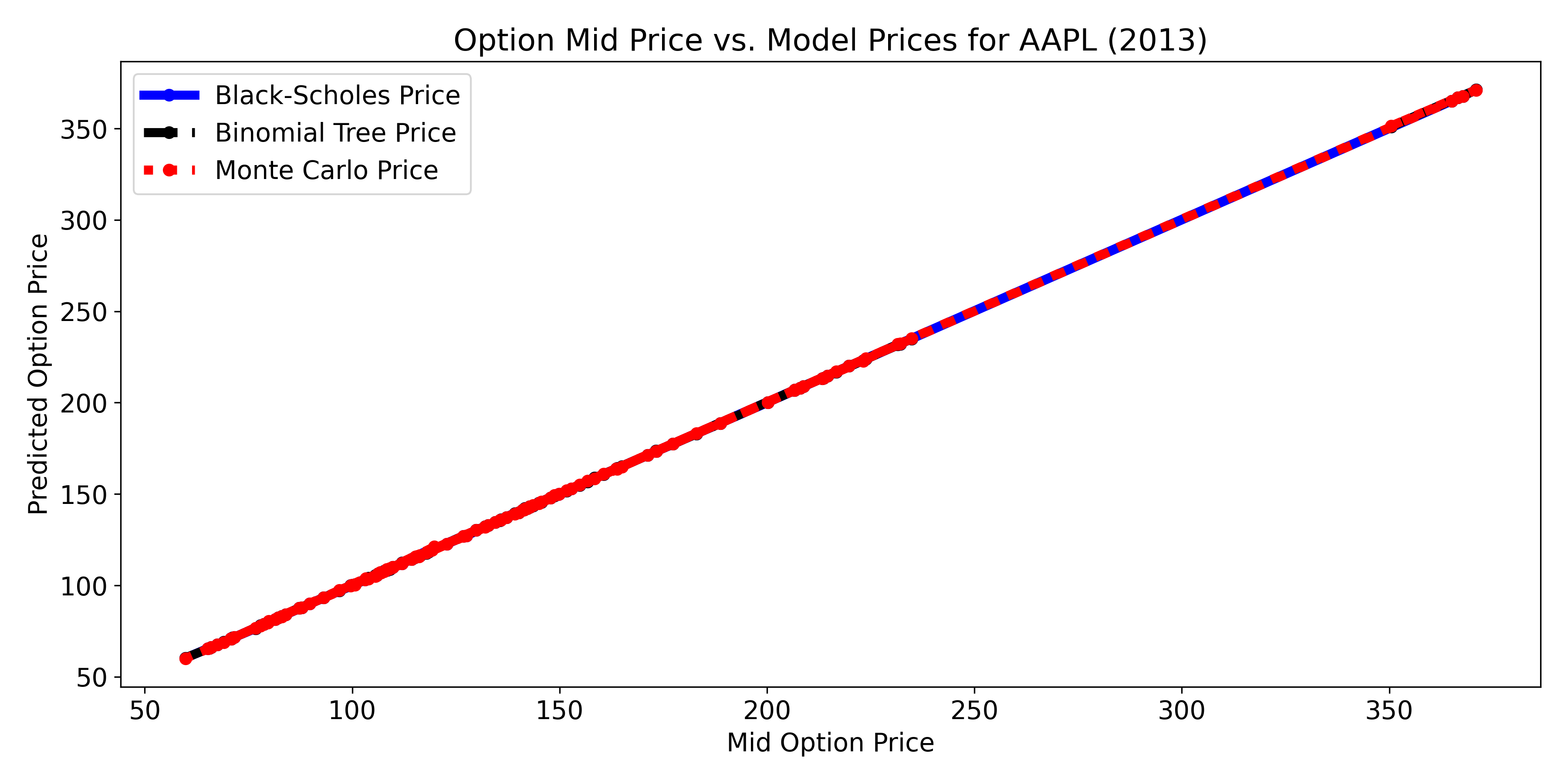
- Comparing the predictions by different models
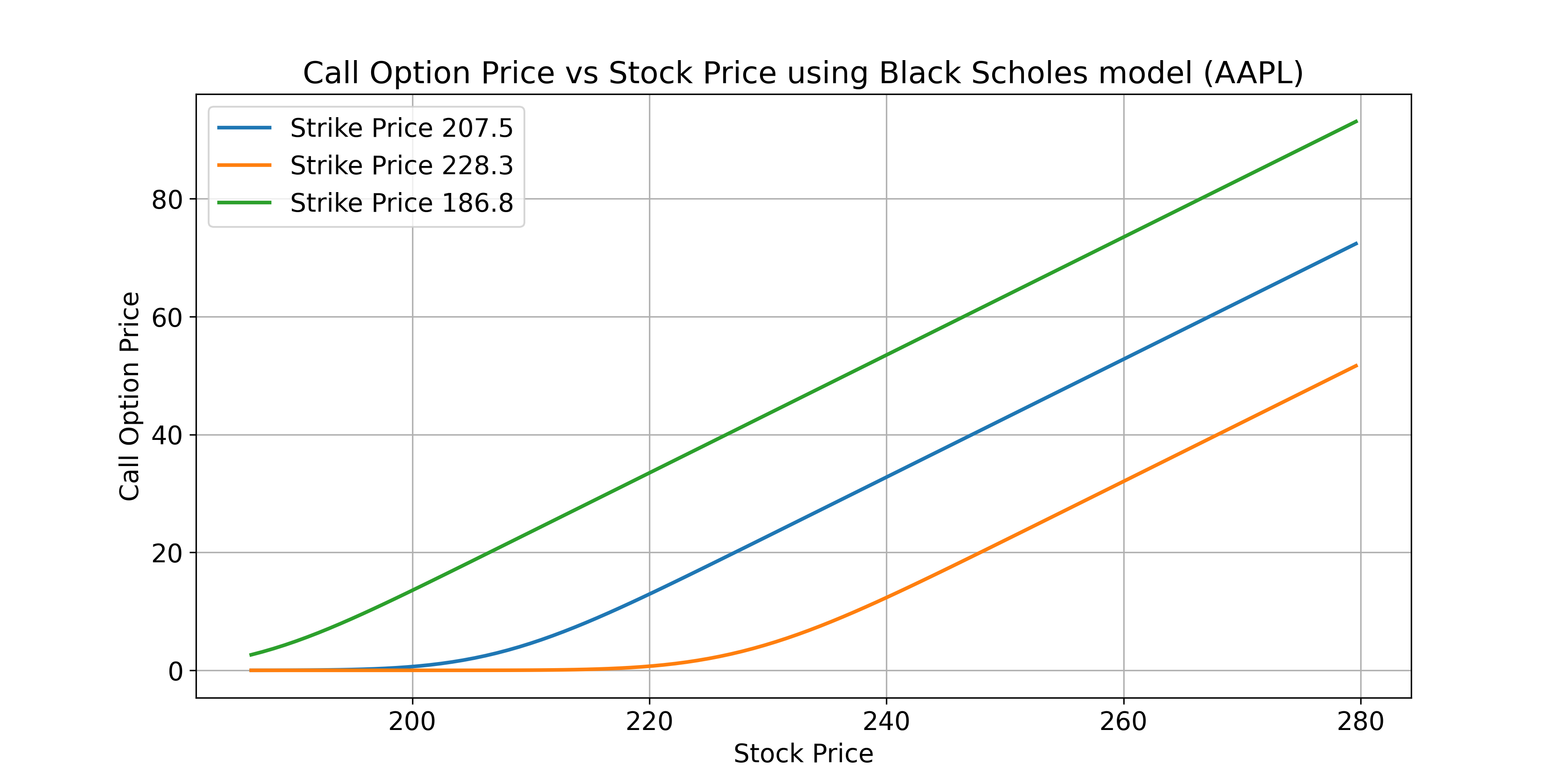
- Option price vs stock price (using Black Scholes model)
- Monte Carlo payoff histogram
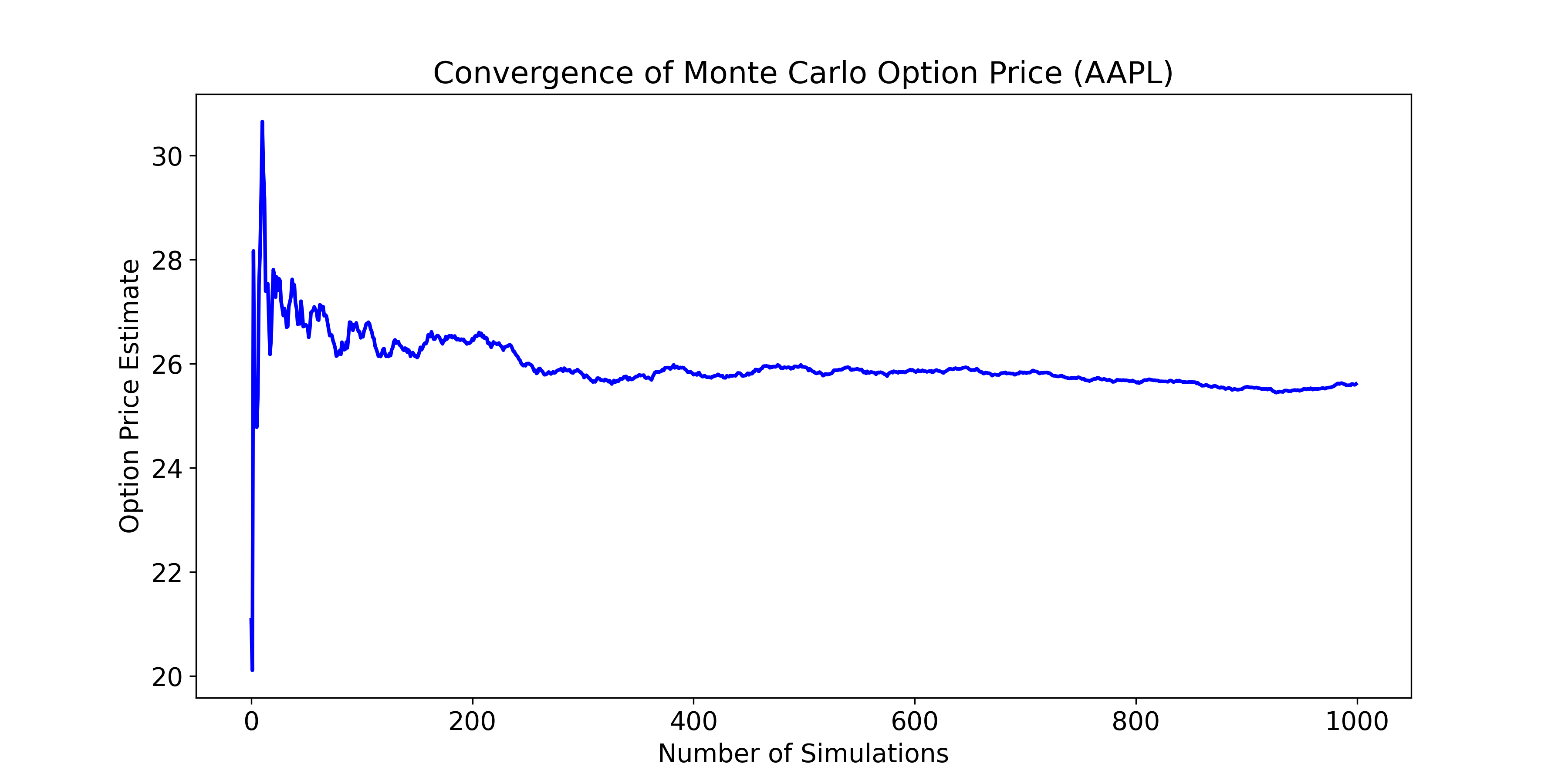
- Monte Carlo convergence plot
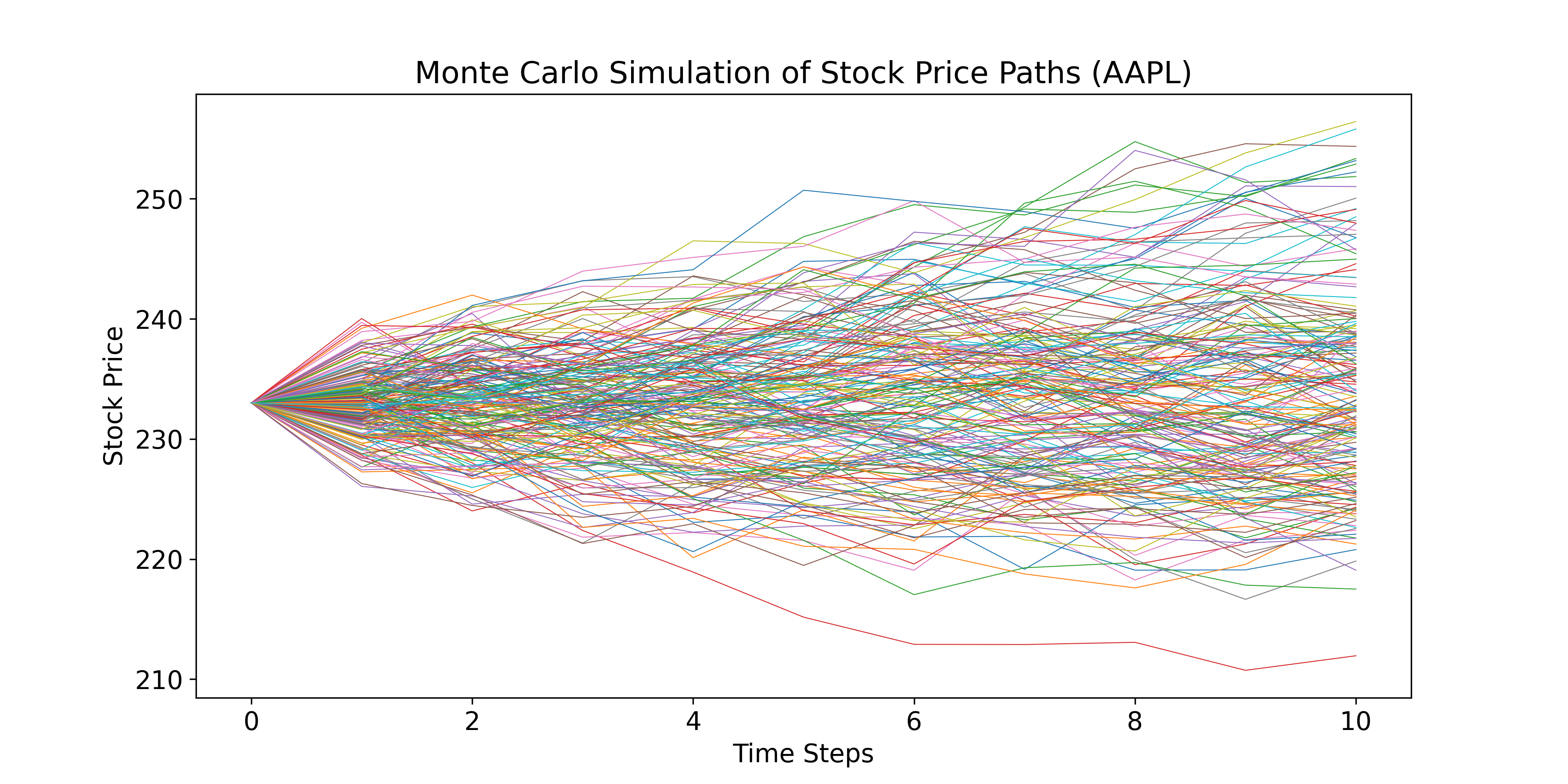
- Monte Carlo paths
Options Pricing and Greeks Calculation Report
1. User Inputs:
- Option type: call
- Stock Ticker: AAPL
- Stock Price (S): 226.5
- Strike Price (K): 207.5
- Days to Expiration: 7 days
- Risk-Free Rate (r): 5.00%
- Market Price of the Option: 22.25
- Start and end date for calculating Historical Volatility: 2023-01-01 - 2024-09-24
2. Calculated Intermediate Values:
- Time to Maturity (T): 0.0192 years
- Historical Volatility (σ): 21.91%
3. Option Prices:
- Option Price (Black-Scholes): 19.17
- Option Price (Monte Carlo): 19.24
- Option Price (Binomial Tree): 19.17
4. Greeks:
- Delta: 0.9983
- Gamma: 0.0008
- Vega: 0.1710
- Theta: -11.3226
- Rho: 3.9682
5. Implied Volatility Calculation:
- Implied Volatility (IV): 82.16%
.
├── option_pricing.py # Main Python script for the project
├── option_pricing_app.py # Streamlit app
├── setup.py # Setup Python script to install the required libraries
├── README.md # This README file
├── output # Output folder containing the reports and plots
You can customise this project by:
- Changing the stock ticker (e.g., from
AAPLtoMSFT). - Modifying the strike price, risk-free rate, time to maturity, or volatility.
- Adjusting the number of simulations for the Monte Carlo method or the number of steps for the Binomial Tree method.
- Clone the repository.
- Install the following Python setup file including the necessary libraries:
python setup.py install- Execute the Python code
option_pricing.pyor the Jupyter Notebook scriptoption_pricing.ipynb.
You can modify the following parameters in the script:
ticker: Ticker symbol of the stock (e.g.,AAPLfor Apple).K: Strike price of the option.T: Time to maturity in years.r: Risk-free rate (annualised).mc_num_sim: Number of simulations for the Monte Carlo method.bt_num_step: Number of steps in the Binomial Tree method.
The Black-Scholes model gives a closed-form solution for pricing call and put options, based on the assumption that stock prices follow a geometric Brownian motion.
For call options:
For put options:
where:
Monte Carlo simulation is used to estimate the price of options by simulating the future stock price paths and calculating the corresponding option payoffs. The method relies on Geometric Brownian Motion (GBM), which models stock price evolution as:
where:
-
$S_t$ is the stock price at time$t$ . -
$r$ is the risk-free interest rate. -
$\sigma$ is the volatility of the stock. -
$\Delta t$ is the time increment (daily or another small step). -
$Z$ is a random variable from a standard normal distribution (representing the random walk).
For each simulation:
- Stock price over time is simulated using the GBM formula.
- Option payoff at maturity is calculated:
-
Call Option:
$\max(0, S_T - K)$ -
Put Option:
$\max(0, K - S_T)$ ,
-
Call Option:
where
- The payoff is discounted back to present value using the risk-free rate:
where
This approach is flexible and can handle a wide variety of option types though it requires many simulations for accuracy.
The Binomial Tree method approximates option prices by constructing a tree of possible future stock prices, calculating option prices by working backwards from the terminal nodes.
- Time is divided to expiration into
nintervals. - Each interval allows the stock price to increase by a factor
uor decrease by a factord. - Option prices are computed by working backwards using risk-neutral probabilities.
-
$\Delta$ : Sensitivity of the option price to changes in the underlying stock price. -
$\Gamma$ : Rate of change of delta with respect to the underlying stock price. -
$\nu$ : Sensitivity of the option price to changes in volatility. -
$\Theta$ : Sensitivity of the option price to time decay. -
$\rho$ : Sensitivity of the option price to changes in the risk-free interest rate.
Implied volatility is derived from the Black-Scholes model to match the market price of an option, calculated through trying Newton-Raphson first, then Bisection, and finally Brent's method. They usually converge to the same solution.
All methods provide alternative means to calculate option prices, especially for options with complex features. Why not running the code and observe the comparison plot?
- Black-Scholes Model - Investopedia
- Monte Carlo Methods - Investopedia
- Binomial Tree Model - Investopedia
- Yahoo Finance API
- Backtesting data source
This project is open-source and available under the MIT License.