机器人技术的一个基本需求是拥有将人类任务的 高级规范 转换 为 如何移动 的 低级描述的算法。
运动规划 和 轨迹规划
机器人运动规划通常忽略动力学和其他差异约束,主要关注 移动目标 所需的平移和旋转。
然而,最近的工作确实考虑了其他方面,例如不确定性,差异约束,建模误差和最优性。
轨迹规划通常指的是从机器人运动规划算法中获取解决方案并确定如何以尊重机器人的机械限制的方式移动解决方案的问题。
A. 运动规划 motion planning
在连续状态空间中进行规划”Planning in Continuous State Spaces
1. 几何表示和转换 Geometric Representations and Transformations
给出了表达运动规划问题的重要背景。
如何构建几何模型,其余部分说明了如何转换它们。
2. 配置空间 Configuration Space
介绍拓扑中的概念,并使用它们来表示配置空间,即运动规划中出现的状态空间。
3.基于采样的运动规划Sampling-Based Motion Planning
近年来在文献中占主导地位的运动规划算法,并已应用于机器人内外的领域。
如果您了解配置空间代表连续状态空间的基本思想,那么大多数概念都应该是可以理解的。
除了运动规划和机器人技术之外,它们甚至适用于出现连续状态空间的其他问题。
4. 组合运动规划Combinatorial Motion Planning
有时称为精确算法,因为它们构建离散表示而不会丢失任何信息。
它们是完整的,这意味着如果存在,它们必须找到解决方案;否则,它们会报告失败。
基于抽样的算法在实践中更有用,但它们只能实现较弱的完整性概念。
5. 基本运动规划的扩展 Extensions of Basic Motion Planning
封闭运动链的规划;
6. 反馈运动规划 Feedback Motion Planning
一个过渡性章节,将 反馈 引入 运动规划问题,但仍未引入 差异约束
侧重于计算开环规划,这意味着规划执行期间可能发生的任何错误都会被忽略
使用反馈产生闭环规划,该规划在执行期间响应不可预测的事件。
B.决策理论规划Decision-Theoretic Planning
在不确定性下进行规划Planning Under Uncertainty。
大部分涉及离散状态空间discrete state spaces,
但是,有些部分涵盖了连续空间的扩展;
1. 基本决策理论Basic Decision Theory
主要思想是为面临其他决策者干预的决策者设计最佳决策。
其他人可能是游戏中真正的对手,也可能是虚构的,以模拟不确定性model uncertainties.
侧重于一步做出决定,并为第三部分提供构建模块,因为在不确定性下的计划可被视为多步决策 multi-step decision making。
2. 顺序决策理论Sequential Decision Theory
通过将一系列基本决策问题链接在一起来扩展它们。
动态编程Dynamic programming 概念在这里变得很重要。
假设当前状态始终是已知的。存在的所有不确定性都与预测未来状态有关,而不是测量当前状态。
3. 传感器和信息空间Sensors and Information Spaces
一个框架,用于在执行期间当前状态未知时进行规划。
关于状态的信息是从传感器观察 和 先前应用的动作的记忆中获得的。
信息空间服务类似检测不确定性问题的目的,因为配置空间具有运动规划。
4. 感知不确定性下的规划Planning Under Sensing Uncertainty
介绍了涉及感知不确定性的几个规划问题和算法。
这包括定位localization,地图构建 map building,pursuit-evasion跟踪? 和 操作 等问题。
所有这些问题都是在信息空间规划的思想下统一起来的.
C. 差异约束下的规划Planning Under Differential Constraints
这里,在运动规划中出现的连续状态空间上可能存在全局(障碍)和局部(差分)约束。
还考虑动态系统,其产生包括位置和速度信息的状态空间(这与控制理论中的状态空间或物理和微分方程中的相空间的概念一致)。
1. 差分模型Differential Models
介绍涉及差异约束的众多模型,
包括车轮滚动产生的约束 以及 机械系统 动力学 产生的约束。
2. 差分约束下的基于抽样的规划 Sampling-Based Planning Under Differential Constraints
所有方法都是基于采样的,因为在差分约束的情况下,组合技术很少能实现。
3. 系统理论和分析技术System Theory and Analytical Techniques
概述了主要在控制理论文献中开发的概念和工具,
通常在差分约束下开发规划算法时提供重要的见解或组成部分。
机器人学 —— 轨迹规划(Configuration Space) A* 或者 DJ 算法
机器人学 —— 轨迹规划(Artificial Potential 人工势场)
一本圣经《Planning Algorithms》伊利诺伊大学教授Lavalle于2006年写的这本书
Filtering and Planning in Information Spaces
A Literature Review of UAV 3D Path Planning 综述论文
sampling-based algorithms 基于采样的算法
node-based algorithms 基于节点的算法
mathematical model based algorithms 基于数学模型的算法
Bio-inspired algorithms 生物启发式算法
multi-fusion based algorithms 多数据融合算法
比较传统的如栅格法、人工势场法、模糊规则等,以及它们相应的改进算法。
路径规划算法发展的历程:
这幅图上的算法罗列的还是很全面的,体现了各个算法的出生顺序。但是并不能很好的对他们进行一个本质的分类。
分类,两大类:
1. 完备的(complete),
(有解是可以求出来的),主要应用于二维三维的grid(栅格),多维的计算量就大了;
2. 基于采样的(sampling-based)又称为概率完备的,
(有解不一定能求出来的,可能经过足够多的采样可以得到解,是概率上的可能能得到解);
Dijstra算法、A*、Theta*
所谓完备就是要达到一个systematic的标准,
即:如果在起始点和目标点间有路径解存在那么一定可以得到解,如果得不到解那么一定说明没有解存在。
这一大类算法在移动机器人领域通常直接在 occupancy grid网格地图 上进行规划(可以简单理解成二值地图的像素矩阵),
以深度优先寻路算法、广度优先寻路算法、Dijkstra(迪杰斯特拉)算法为始祖,
以A*算法(Dijstra算法上以减少计算量为目的加上了一个启发式代价)最为常用,
近期的Theta*算法是在A*算法的基础上增加了line-of-sight优化使得规划出来的路径不完全依赖于单步的栅格形状,
答主以为这个算法意义不大,不就是规划了一条路径再简单平滑了一下么
完备的算法的优势在与它对于解的捕获能力是完全的,但是由此产生的缺点就是算法复杂度较大。
这种缺点在二维小尺度栅格地图上并不明显,但是在大尺度,尤其是多维度规划问题上,
比如机械臂、蛇形机器人的规划问题将带来巨大的计算代价。
这样也直接促使了第二大类算法的产生。
这种算法一般是不直接在grid地图进行最小栅格分辨率的规划,
它们采用在地图上随机撒一定密度的粒子来抽象实际地图辅助规划。
如PRM算法及其变种就是在原始地图上进行撒点,抽取roadmap在这样一个拓扑地图上进行规划;
RRT以及其优秀的变种RRT-connect则是在地图上每步随机撒一个点,
迭代生长树的方式,连接起止点为目的,最后在连接的图上进行规划。
这些基于采样的算法速度较快,但是生成的路径代价(可理解为长度)较完备的算法高,
而且会产生“有解求不出”的情况(PRM的逢Narrow space卒的情况)。
这样的算法一般在高维度的规划问题中广泛运用。
除了这两类之外还有
间接的规划算法:Experience-based(Experience Graph经验图算法)算法:基于经验的规划算法,
这是一种存储之前规划路径,建立知识库,依赖之进行规划的方法,题主有兴趣可以阅读相关文献。
这种方法牺牲了一定的空间代价达到了速度与完备兼得的优势。
此外还有基于广义Voronoi图的方法进行的Fast-marching规划,类似dijkstra规划和势场的融合,
该方法能够完备地规划出位于道路中央,远离障碍物的路径。
APF(人工势场)算法,
至于D* 、势场法、DWA(动态窗口法)、SR-PRM,
属于在动态环境下为躲避动态障碍物、考虑机器人动力学模型设计的规划算法。
最后推荐一本圣经《Planning Algorithms》伊利诺伊大学教授Lavalle于2006年写的这本书,可以网上看看英文原版的
http://planning.cs.uiuc.edu/booka4.pdf
Dijkstra算法和A*算法都是最短路径问题的常用算法,下面就对这两种算法的特点进行一下比较。
1.Dijkstra算法计算源点到其他所有点的最短路径长度,A*关注点到点的最短路径(包括具体路径)。
2.Dijkstra算法建立在较为抽象的图论层面,A*算法可以更轻松地用在诸如游戏地图寻路中。
3.Dijkstra算法的实质是广度优先搜索,是一种发散式的搜索,所以空间复杂度和时间复杂度都比较高。
对路径上的当前点,A*算法不但记录其到源点的代价,还计算当前点到目标点的期望代价,
是一种启发式算法,也可以认为是一种深度优先的算法。
4.由第一点,当目标点很多时,A*算法会带入大量重复数据和复杂的估价函数,
所以如果不要求获得具体路径而只比较路径长度时,Dijkstra算法会成为更好的选择
这里列出,是因为它代表了一大类基于采样的路径规划方法。PRM是一种多查询(multiple-query)方法:先通过采样,在位姿空间中建里roadmap,然后利用A*或类A*算法在roadmap上查询路径。所以,这种方法的核心不在于寻路,而在于如何采样并在此基础上建立roadmap。roadmap可以复用,这就是“multiple-query”的含义。有人将PRM改造成单查询(single-query)方法,即不必在整个位姿空间中采样(像多查询方法那样在整个位姿空间中采样是非常耗时的),因为单查询主要解决的是“一次性”问题:每次查询仅仅进行局部采样,原则是“够用就好”。因为采样不均导致有些路径明明存在却规划不到的现象时有存在,这类经典问题叫做narrow passage,针对这些问题,有很多PRM变体被提出,这里不赘述了。
只不过这个旧瓶能装各种各样的新酒,所以列出来。RRT算法家族是恐怕目前是最经典的一类基于采样的单查询方法了。
用RRT做路径规划的过程如下:分别以位姿空间中的起始点和目标点为根,同时生成两棵树,每次给它们一个随机增量,
让它们相向生长,直到它们合并在一起。树的“长速”非常快,很快就能覆盖起始点和目标点之间的位姿空间,
于是得名Rapid exploring rand tree。树长好之后,路径自然也就得到了:对于一棵树,从起始点到目标点有且只有一条路径。
RRT算法是RRT算法的变种算法,算法可以收敛到最优解,不仅可以实现二维环境下的路径规划,
多维度的环境也可以使用RRT算法,而且由于算法是均匀采样,并不会出现局部最小的情况。
RPM 要先构建roadmap,因此可以多次使用的,graph中的node还可以相互连接的
RRT是直接从start node延增出去的,每个node只有一个parent的。
从名字可以看出,它们分别基于PRM和RRT——这也是我首先列出PRM和RRT的原因——同时,
它们分别是PRM和RRT的渐进最优(asymptotically optimal)形式。PRM*与PRM的主要区别是选择最近邻的方法不同。
在建立roadmap时,每个采样点都要尝试和它邻域内的k个最近采样点建立连接,PRM的邻域半径r是固定的,
而PRM*的领域半径r是采样点数量n的函数,n越大,r越小。对原始RRT算法稍加修改,
可以得到RRG(Rapidly-exploring Random Graph)。每当新生成一个采样点,RRT和RRG都要将这个点和树上距它最近的点相连,
于是这个点就被加到了树中;不同之处在于,RRG还需要尝试连接新采样点和它邻域中的所有采样点,
所以,RRG中可能包含环路,RRG是一个图。RRT*是RRG的一个变体。
与RRG不同,RRT*并不会将新采样点和树上距它最近的点相连,
而是在尝试连接新采样点和它邻域中的所有采样点时,保留cost最小的那个连接。
这里的cost是指机器人从树的根节点运动到新采样点的代价,可以是距离代价,也可以是其他代价。
假设新采样点为P1,连接到的邻域采样点为P2,如果发现从根节点到P1的cost与从P1到P2的cost之和比从根节点到P2的cost小,
则将P1作为P2的新parent。同时将P2和它的原parent之间的边删除,将P1和P2之间的边加入树中。
这个算法被用到了NASA的火星车上,所以非常值得一提。
D*的含义是“Dynamic A*”,可见它和A*是有渊源的。D*的优势在于高效的重规划。
一旦环境发生改变,从头规划一条新路径是很耗时的,
D*则只进行局部重规划,所以之前规划出的部分路径可以复用。
D*有个同宗兄弟叫做D* Lite,它不是D*的变体,但是它的效果和D*一样。
构造一个函数 = an attractive potential field + a repulsive potential field
= 一个离目标点越近能量越低的函数 + 一个离障碍物越远能量越低的函数
下面
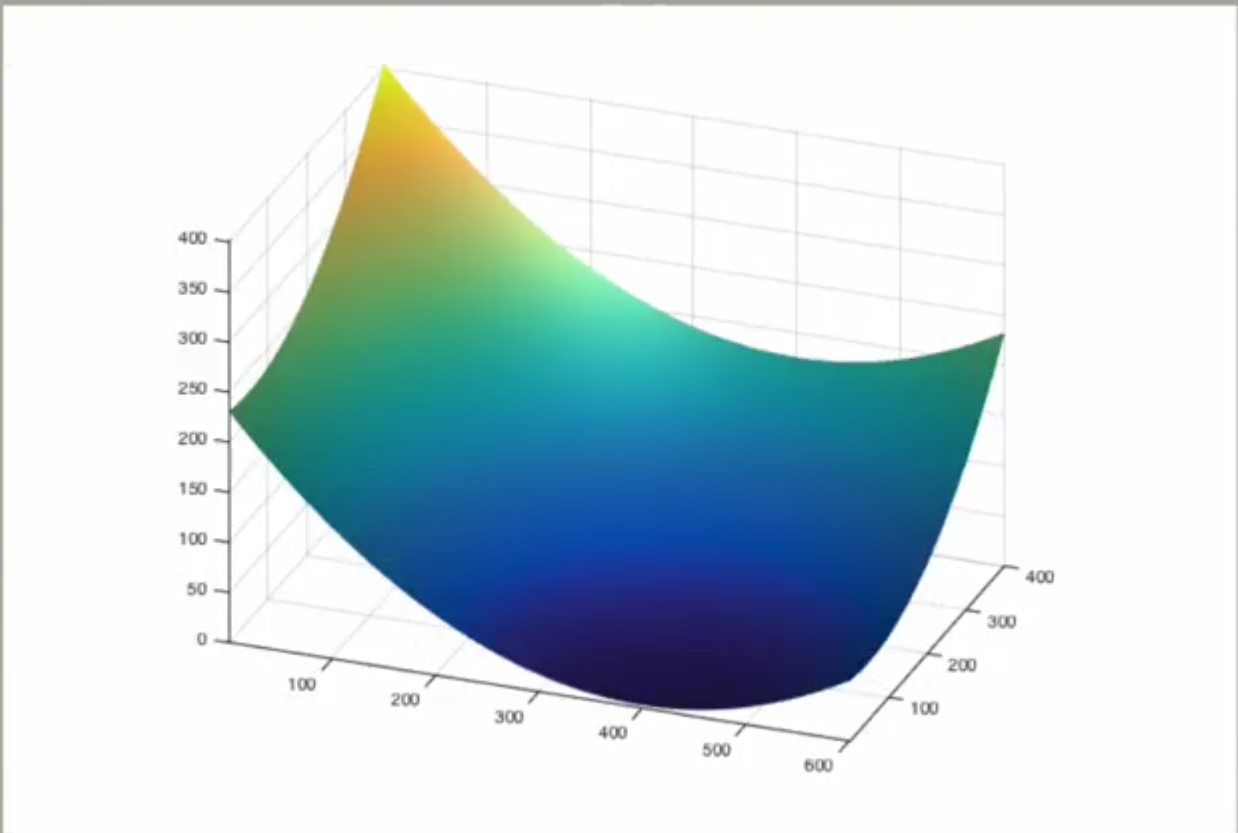
第一张图是黑色障碍物,
第二张图是attractive potential field ,
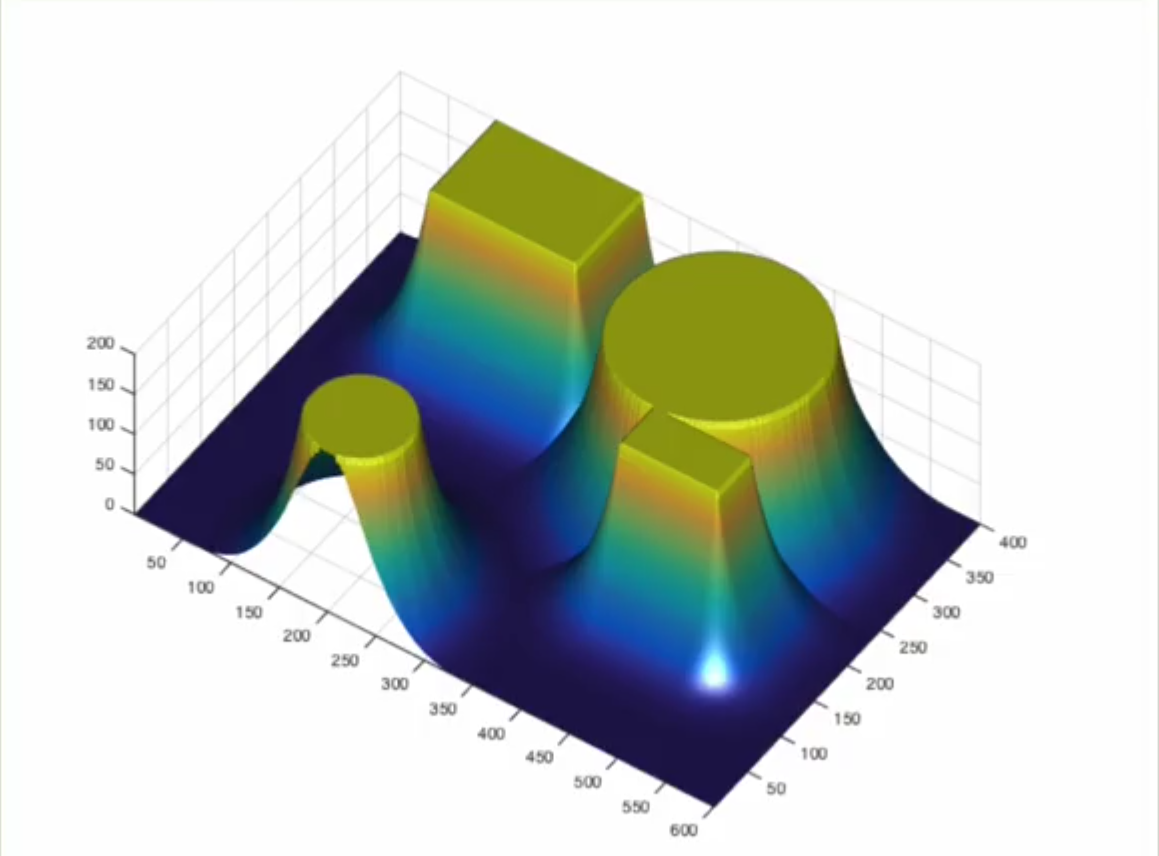
第三张图是 repulsive potential field,
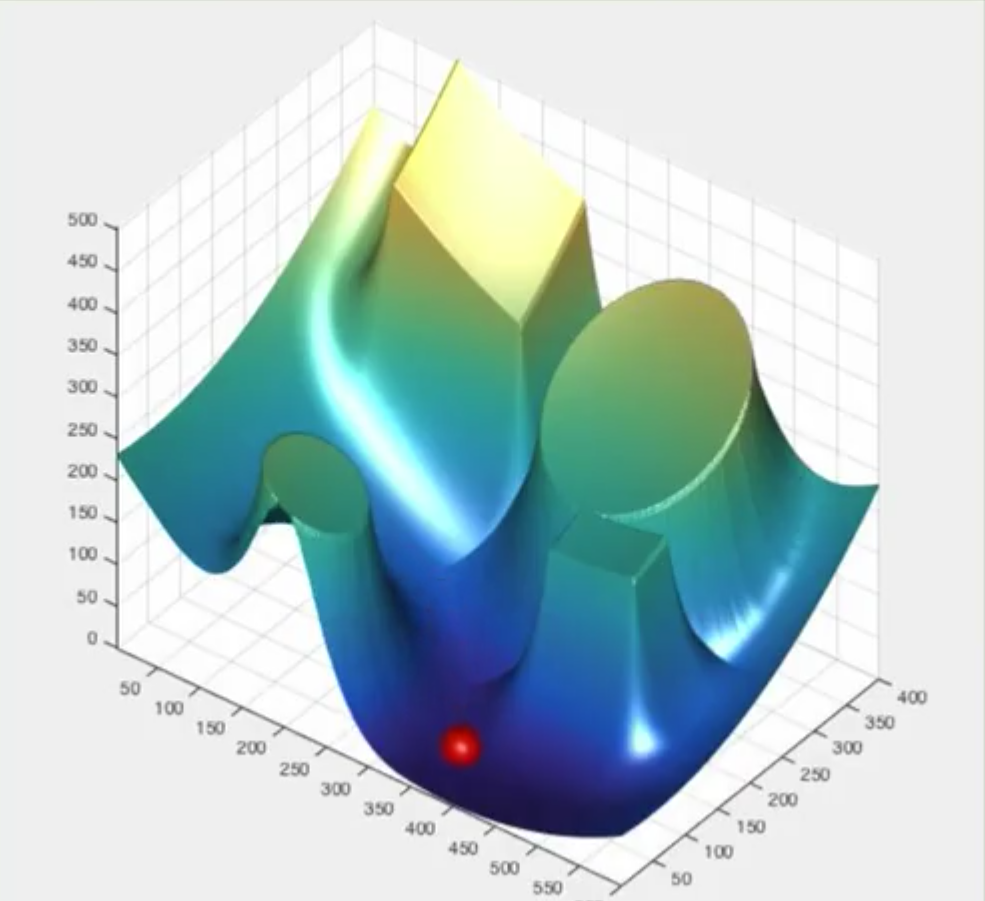
最后一张是上面两个的相加得到的最终构造的函数。
可能会陷入到local minimum 局部最小值
ethz 开源的一个路径规划算法库
需要的是里程计tf坐标变换和3d点云数据,计算下个位置的gain,这
个gain也考虑了octomap中格子的概率,考虑的是看到还没有mapped的格子
,尽可能寻找相应多的格子进行路径规划,
代码中的mesh_structure.h,对我们的作用不是很大,主要是用于导入CAD图纸,
不用在线输入点云数据,这时候寻找的是看到的surface最多的下一个目标点
工具显示的第三个维度是概率的大小,可视化,针对的是moveit这个开源工具,没有试过别的可不可以