[TOC]
PPO算法(Proximal Policy Optimization Algorithms)于2017年由John Schulman提出,是一种基于策略优化的强化学习算法。PPO算法易于实现且在许多任务上取得了很好的效果,是目前强化学习领域的主流算法之一。PPO最主要的优点是:
- 算法简单,易于实现,且在许多任务上取得了很好的效果。
- 允许对采样得到的数据进行多次利用,从而提高数据的利用效率,降低了样本复杂度(sample complexity)。
- 其优化目标对策略更新进行了约束,使得策略更新的幅度受到限制,从而避免了策略更新过大导致的性能下降或训练不稳定,这正是其名称中Proximal的含义。
类比于登山,每个箭头表示一次策略更新,箭头越长表示更新幅度越大。显然,黄色箭头式的小幅迭代更新更可能到达山顶。黄色代表稳重,粉红色代表激进。
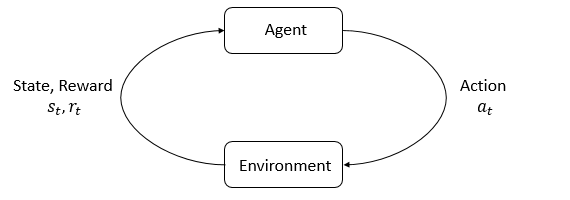
在进入正题前,我们先简要回顾下RL的基本概念。在强化学习中,智能体(Agent)通过与环境(Environment)交互,观察环境的状态(State:
- 策略(Policy):策略是在某个状态下选择动作的概率分布,通常用$\pi_\theta(a|s)$表示。
- 轨迹(Trajectory):轨迹是从初始状态到终止状态的状态、动作、奖励序列,通常用$\tau = (s_0, a_0, r_0, s_1, a_1, r_1, \cdots)$表示。
- 回报(Return):回报是在轨迹中获得的折算奖励的总和,通常用$R(\tau) = \sum_{t=0}^T \gamma^t r_t$表示。
- 价值函数(Value Function):价值函数是状态$s$的期望回报,通常用$V(s)=\mathbb{E}_{\tau \sim \pi} [R(\tau) | s_0 = s]$表示。
- 动作价值函数(Action Value Function):动作价值函数是在状态$s$下执行动作$a$的期望回报,通常用$Q(s, a)=\mathbb{E}_{\tau \sim \pi} [R(\tau) | s_0 = s, a_0 = a]$表示。
- 优势函数(Advantage Function):优势函数是在状态$s$下执行动作$a$的期望回报相对于价值函数的差值,其朴素形式为$A(s, a) = Q(s, a) - V(s)$,后面我们会介绍Generalized Advantage Estimation。
首先我们令将要更新的策略和更新之前的策略的比值为$r_t(\theta) = \frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$,则PPO试图最大化的优化目标Clipped Surrogate Objective为:
$$
L^{CLIP}(\theta) = \mathbb{E}_{t} \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) A_t \right) \right]
$$
我们对一个时间步的$\min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) A_t \right)$进行分析,可以得到下图:

当$A>0$时,最大化$L^{CLIP}$可以使$r$变大,对应于小红点从左下方向右上方移动,但是不会超过$1+\epsilon$(超出部分发生截断);当$A<0$时,最大化$L^{CLIP}$可以使$r$变小,对应于小红点从右下方向左上方移动,但是不会超过$1-\epsilon$(超出部分发生截断)。这样,PPO算法就可以保证策略更新的幅度受到限制,总是不会偏离旧策略$\pi_{\theta_{old}}$太远。为方便理解,我们也可以通过下表来展示上述结论:
| Return Value of |
Objective is Clipped | Sign of Objective | Gradient | ||
|---|---|---|---|---|---|
| + | no | + | ✓ | ||
| - | no | - | ✓ | ||
| + | no | + | ✓ | ||
| - | yes | - | 0 | ||
| + | yes | + | 0 | ||
| - | no | - | ✓ |
算法中假设我们可以跑N个actor,每个actor采样T个时间步,总共得到NT个时间步的数据。值得注意的是,由于PPO算法策略更新的幅度不大,可以多次利用采样得到的数据进行梯度更新(
记TD residual为$\delta_t^{V} = r_t + \gamma V(s_{t+1}) - V(s_t)$,我们可以得到$k$时间步展开的优势函数$\hat{A}t^{(k)}$: $$ \begin{align*} \hat{A}t^{(1)} &:= \delta^{V}t &&= -V(s_t) + r_t + \gamma V(s{t+1}) \ \hat{A}t^{(2)} &:= \delta^{V}t + \gamma \delta^{V}{t+1} &&= -V(s_t) + r_t + \gamma r{t+1} + \gamma^2 V(s{t+2}) \ \hat{A}t^{(3)} &:= \delta^{V}t + \gamma \delta^{V}{t+1} + \gamma^2 \delta^{V}{t+2} &&= -V(s_t) + r_t + \gamma r{t+1} + \gamma^2 r_{t+2} + \gamma^3 V(s_{t+3}) \ & \vdots \ \hat{A}t^{(k)} &:= \sum{l=0}^{k-1} \gamma^l \delta^{V}{t+l} &&= -V(s_t) + r_t + \gamma r{t+1} + \dots + \gamma^{k-1} r_{t+k-1} + \gamma^k V(s_{t+k}) \ \hat{A}t^{(\infty)} &:= \sum{l=0}^{\infty} \gamma^l \delta^{V}{t+l} &&= -V(s_t) + \sum{l=0}^{\infty} \gamma^l r_{t+l}, \end{align*} $$ 对这些项取指数加权平均,我们即得到GAE的表达式:
$$ \begin{align*} \hat{A}t^{\text{GAE}(\gamma, \lambda)} &:= (1 - \lambda) \left( \hat{A}t^{(1)} + \lambda \hat{A}t^{(2)} + \lambda^2 \hat{A}t^{(3)} + \dots \right) \ &= (1 - \lambda) \left( \delta^{V}t + \lambda (\delta^{V}t + \gamma \delta^{V}{t+1}) + \lambda^2 (\delta^{V}t + \gamma \delta^{V}{t+1} + \gamma^2 \delta^{V}{t+2}) + \dots \right) \ &= (1 - \lambda) \left( \delta^{V}t (1 + \lambda + \lambda^2 + \dots) + \gamma \delta^{V}{t+1} (\lambda + \lambda^2 + \lambda^3 + \dots) \right. \ & \qquad \left. + \gamma^2 \delta^{V}{t+2} (\lambda^2 + \lambda^3 + \lambda^4 + \dots) + \dots \right) \ &= (1 - \lambda) \left( \delta^{V}t \left( \frac{1}{1 - \lambda} \right) + \gamma \delta^{V}{t+1} \left( \frac{\lambda}{1 - \lambda} \right) + \gamma^2 \delta^{V}{t+2} \left( \frac{\lambda^2}{1 - \lambda} \right) + \dots \right) \ &= \sum{l=0}^{\infty} (\gamma \lambda)^l \delta^{V}{t+l} \end{align*} $$
我们用一个python文件实现了完整的PPO算法,GAE的计算,mlp,cnn,离散及连续动作的actor,以及CartPole和乒乓球两个游戏的学习及动画效果,仅依赖pytorch和gymnasium(gym),总共400多行代码:https://github.com/schinger/PPO-simplest
策略为actor,价值函数为critic,我们用神经网络mlp或cnn来拟合这两个函数,合为ac。用类PPOBuffer来存储采样数据(轨迹),计算GAE及回报。ppo算法实现为一个函数。Policy Loss为:
pi, logp = ac.pi(obs, act)
ratio = torch.exp(logp - logp_old)
clip_adv = torch.clamp(ratio, 1-clip_ratio, 1+clip_ratio) * adv
loss_pi = -(torch.min(ratio * adv, clip_adv)).mean()Value Function Loss 为:
((ac.v(obs) - ret)**2).mean()这是一个连续动作actor的例子,我们采用高斯分布GaussianActor来建模动作分布,将标准差对角化并将其对数设为模型的参数 log_std,用神经网络去预测均值mu_net。用CPU训练几分钟即可完全掌握这个游戏。
这是一个离散动作actor的例子,我们采用softmax分布CategoricalActor来建模动作分布。这个例子从像素点开始学习,我们利用类FramePreStacking来将连续的n帧图像堆叠起来,预处理得到类似位置,速度,加速度等信息(用差分来近似),然后用CNN网络cnn来进一步提取特征。用GPU训练几小时即可击败内置AI。
另外附上一个Vanilla Policy Gradients的实现,仅基于numpy,手工计算梯度,共一百来行代码,供参考:https://github.com/schinger/pong_actor-critic
近年来PPO的大火主要是因为LLM中RLHF(Reinforcement Learning from Human Feedback)首先应用的是PPO,我们也实现了训练LLama的PPO算法,仅依赖于pytorch,不调用其他包:https://github.com/schinger/FullLLM 。
然而值得指出的是,PPO算法并不是在所有场景下都是最优的,比如在LLM中,有研究指出,Vanilla Policy Gradients(Reinforce)在LLM中表现更好。
PPO源于对TRPO的简化。在TRPO这篇论文中,作者先推导出了一个理论上保证期望回报单调递增的策略迭代算法(即,论文中的Algorithm 1),然后经过参数化和近似,得到了约束目标的采样估计,最后,经过重要性采样估计(Importance Sampling Estimator),用$q$表示采样分布,得到下式: $$ \sum_a \pi_\theta(a|s_n) A_{\theta_{\text{old}}}(s_n, a) = \mathbb{E}{a \sim q} \left[ \frac{\pi\theta(a|s_n)}{q(a|s_n)} A_{\theta_{\text{old}}}(s_n, a) \right] $$ 如果另$q = \pi_{\theta_{\text{old}}}$,再将TRPO的KL约束条件简化为PPO的Clip约束,即可得到PPO算法,所以PPO是TRPO的简化(trick of clip function),它避免了TRPO中复杂的约束优化问题 (need to use the conjugate gradient algorithm (Hessian-vector products) followed by a line search),在主流机器学习框架中易于实现,所以流传更广。
另外,我们可以从梯度的视角来看待PPO算法与vanilla policy gradients的关系。在vanilla policy gradients中,策略梯度为: $$ \hat{g} = {\mathbb{E}}t \left[ \nabla\theta \log \pi_\theta(a_t | s_t) {A}t \right] = {\mathbb{E}}t \left[ \frac{\nabla\theta \pi\theta(a_t | s_t)}{\pi_\theta(a_t | s_t)} {A}t \right] $$ 不带clip的PPO算法的梯度为: $$ \hat{g} = \nabla\theta \mathbb{E}t \left[ \frac{\pi\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)} A_t \right] = \mathbb{E}t \left[ \frac{\nabla\theta \pi_\theta(a_t|s_t)}{\pi_{\theta_{\text{old}}}(a_t|s_t)} A_t \right] $$ 两者在$\pi_\theta(a_t|s_t) = \pi_{\theta_{\text{old}}}(a_t|s_t)$时相等。但是在$\pi_\theta(a_t|s_t) \neq \pi_{\theta_{\text{old}}}(a_t|s_t)$,且二者向超过一定的分歧迈进时,PPO的梯度会被置零(见上文表格),即避免了策略更新的幅度过大,提高了训练的稳定性。