Time series symbolic discretization with SAX

This code is released under GPL v.2.0 and implements in Python:

• Symbolic Aggregate approXimation (i.e., SAX) toolkit stack (zNormalization, PAA, SAX) [1]
• EMMA -- an algorithm for time series motif discovery [2]
• HOT-SAX - a time series anomaly (discord) discovery algorithm [3]

[1] Lin, J., Keogh, E., Patel, P., and Lonardi, S., Finding Motifs in Time Series, The 2nd Workshop on Temporal Data Mining, the 8th ACM Int'l Conference on KDD (2002)

[2] Patel, P., Keogh, E., Lin, J., Lonardi, S., Mining Motifs in Massive Time Series Databases, In Proc. ICDM (2002)

[3] Keogh, E., Lin, J., Fu, A., HOT SAX: Efficiently finding the most unusual time series subsequence, In Proc. ICDM (2005)

Note that all of the library's functionality is also available in R and Java

Citing this work:

If you are using this implementation for you academic work, please cite our Grammarviz 2.0 paper:

[Citation] Senin, P., Lin, J., Wang, X., Oates, T., Gandhi, S., Boedihardjo, A.P., Chen, C., Frankenstein, S., Lerner, M., GrammarViz 2.0: a tool for grammar-based pattern discovery in time series, ECML/PKDD Conference, 2014.

0.0 SAX transform in a nutshell

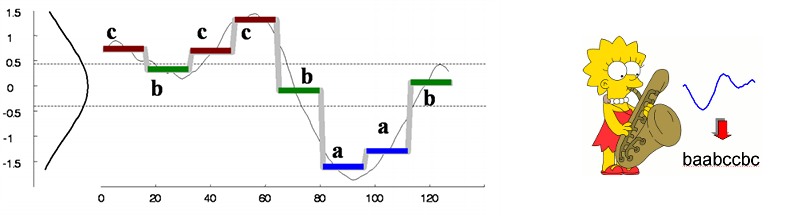
SAX is used to transform a sequence of rational numbers (i.e., a time series) into a sequence of letters (i.e., a string). An illustration of a time series of 128 points converted into the word of 8 letters:

As discretization is probably the most used transformation in data mining, SAX has been widely used throughout the field. Find more information about SAX at its authors pages: SAX overview by Jessica Lin, Eamonn Keogh's SAX page, or at sax-vsm wiki page.

1.0 Building

The code is written in Python and hosted on PyPi, so use pip to install it. This is what happens in my clean test environment:

$ pip install saxpy
Collecting saxpy
Downloading saxpy-1.0.0.dev154.tar.gz (180kB)
	100% |████████████████████████████████| 184kB 778kB/s 
Requirement already satisfied: numpy in /home/psenin/anaconda3/lib/python3.6/site-packages (from saxpy)
Requirement already satisfied: pytest in /home/psenin/anaconda3/lib/python3.6/site-packages (from saxpy)
...
Installing collected packages: coverage, pytest-cov, codecov, saxpy
Successfully installed codecov-2.0.15 coverage-4.5.1 pytest-cov-2.5.1 saxpy-1.0.0.dev154

2.0 Simple time series to SAX conversion

To convert a time series of an arbitrary length to SAX we need to define the alphabet cuts. Saxpy retrieves cuts for a normal alphabet (we use size 3 here) via cuts_for_asize function:

from saxpy.alphabet import cuts_for_asize
cuts_for_asize(3)

which yields an array:

array([      -inf, -0.4307273,  0.4307273])

To convert a time series to letters with SAX we use ts_to_string function but not forgetting to z-normalize the input time series (we use Normal alphabet):

import numpy as np
from saxpy.znorm import znorm
from saxpy.sax import ts_to_string
ts_to_string(znorm(np.array([-2, 0, 2, 0, -1])), cuts_for_asize(3))

this produces a string:

'abcba'

3.0 Time series to SAX conversion with PAA aggregation (i.e., by "chunking")

In order to reduce dimensionality further, the PAA (Piecewise Aggregate Approximation) is usually applied prior to SAX:

import numpy as np
from saxpy.znorm import znorm
from saxpy.paa import paa
from saxpy.sax import ts_to_string

dat = np.array([-2, 0, 2, 0, -1])
dat_znorm = znorm(dat)
dat_paa_3 = paa(dat_znorm, 3)

ts_to_string(dat_paa_3, cuts_for_asize(3))

and three-letters string is produced:

'acb'

4.0 Time series to SAX conversion via sliding window

Typically, in order to investigate the input time series structure in order to discover anomalous (i.e., discords) and recurrent (i.e., motifs) patterns we employ time series to SAX conversion via sliding window. Saxpy implements this workflow

import numpy as np
from saxpy.sax import sax_via_window

dat = np.array([0., 0., 0., 0., 0., -0.270340178359072, -0.367828308500142,
            0.666980581124872, 1.87088147328446, 2.14548907684624,
            -0.480859313143032, -0.72911654245842, -0.490308602315934,
            -0.66152028906509, -0.221049033806403, 0.367003418871239,
            0.631073992586373, 0.0487728723414486, 0.762655178750436,
            0.78574757843331, 0.338239686422963, 0.784206454089066,
            -2.14265084073625, 2.11325193044223, 0.186018356196443,
            0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.519132472499234,
            -2.604783141655, -0.244519550114012, -1.6570790528784,
            3.34184602886343, 2.10361226260999, 1.9796808733979,
            -0.822247322003058, 1.06850578033292, -0.678811824405992,
            0.804225748913681, 0.57363964388698, 0.437113583759113,
            0.437208643628268, 0.989892093383503, 1.76545983424176,
            0.119483882364649, -0.222311941138971, -0.74669456611669,
            -0.0663660879732063, 0., 0., 0., 0., 0.,])

sax1 = sax_via_window(dat, 6, 3, 3, "none", 0.01)

sax1

the result is represented as a data structure of resulting words and their respective positions on time series:

defaultdict(list,
        {'aac': [4, 10, 11, 30, 35],
         'abc': [12, 14, 36, 44],
         'acb': [5, 16, 21, 37, 43],
         'acc': [13, 52, 53],
         'bac': [3, 19, 34, 45, 51],
         'bba': [31],
         'bbb': [15, 18, 20, 22, 25, 26, 27, 28, 29, 41, 42, 46],
         'bbc': [2],
         'bca': [6, 17, 32, 38, 47, 48],
         'caa': [8, 23, 24, 40],
         'cab': [9, 50],
         'cba': [7, 39, 49],
         'cbb': [33],
         'cca': [0, 1]})

sax_via_window is parameterised with a sliding window size, desired PAA aggregation, alphabet size, z-normalization threshold, and a numerosity reduction strategy as follows:

def sax_via_window(series, win_size, paa_size, alphabet_size=3,
               nr_strategy='exact', z_threshold=0.01)

5.0 Time series discord discovery with HOT-SAX

Saxpy implements HOT-SAX discord discovery algorithm in find_discords_hotsax function which can be used as follows:

import numpy as np
from saxpy.hotsax import find_discords_hotsax
from numpy import genfromtxt
dd = genfromtxt("data/ecg0606_1.csv", delimiter=',')  
discords = find_discords_hotsax(dd)
discords

and discovers anomalies easily:

[(430, 5.2790800061718386), (318, 4.1757563573086953)]

The function has a similar parameterization: sliding window size, PAA and alphabet sizes, z-normalization threshold, and a parameter specifying how many discords are desired to be found:

def find_discords_hotsax(series, win_size=100, num_discords=2, a_size=3,
                     paa_size=3, z_threshold=0.01)

Saxpy also provides a brute-force implementation of the discord search if you'd like to verify discords or evaluate the speed-up:

find_discords_brute_force(series, win_size, num_discords=2,
                          z_threshold=0.01)

which can be called as follows:

discords = find_discords_brute_force(dd[100:500], 100, 4)
discords

[(73, 6.198555329625453), (219, 5.5636923991016136)]

6.0 Time series motif discovery with EMMA

ToDo...

Made with Aloha!