Time series symbolic discretization with SAX

This code is released under GPL v.2.0 and implements in Python:

• Symbolic Aggregate approXimation (i.e., SAX) toolkit stack [1]
• a function for time series motif discovery (EMMA) [2]
• HOT-SAX - a time series anomaly (discord) discovery algorithm [3]

[1] Lin, J., Keogh, E., Patel, P., and Lonardi, S., Finding Motifs in Time Series, The 2nd Workshop on Temporal Data Mining, the 8th ACM Int'l Conference on KDD (2002)

[2] Patel, P., Keogh, E., Lin, J., Lonardi, S., Mining Motifs in Massive Time Series Databases, In Proc. ICDM (2002)

[3] Keogh, E., Lin, J., Fu, A., HOT SAX: Efficiently finding the most unusual time series subsequence, In Proc. ICDM (2005)

Note that the most of the library's functionality is also available in R and Java

Citing this work:

If you are using this implementation for you academic work, please cite our Grammarviz 2.0 paper:

[Citation] Senin, P., Lin, J., Wang, X., Oates, T., Gandhi, S., Boedihardjo, A.P., Chen, C., Frankenstein, S., Lerner, M., GrammarViz 2.0: a tool for grammar-based pattern discovery in time series, ECML/PKDD Conference, 2014.

0.0 SAX transform in a nutshell

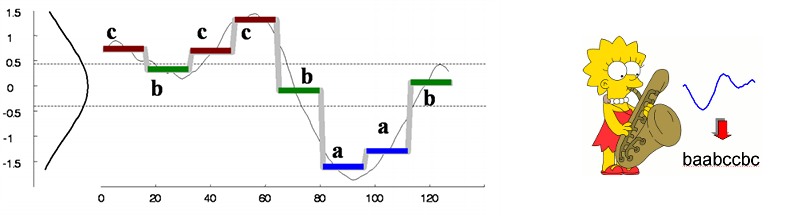
SAX is used to transform a sequence of rational numbers (i.e., a time series) into a sequence of letters (i.e., a string). An illustration of a time series of 128 points converted into the word of 8 letters:

As discretization is probably the most used transformation in data mining, SAX has been widely used throughout the field. Find more information about SAX at its authors pages: SAX overview by Jessica Lin, Eamonn Keogh's SAX page, or at sax-vsm wiki page.

1.0 Building

The code is written in Python and hosted on PyPi, so use pip to install it. This is what happens in my clean test environment:

$ pip install saxpy
Collecting saxpy
Downloading saxpy-1.0.0.dev154.tar.gz (180kB)
	100% |████████████████████████████████| 184kB 778kB/s 
Requirement already satisfied: numpy in /home/psenin/anaconda3/lib/python3.6/site-packages (from saxpy)
Requirement already satisfied: pytest in /home/psenin/anaconda3/lib/python3.6/site-packages (from saxpy)
...
Installing collected packages: coverage, pytest-cov, codecov, saxpy
Successfully installed codecov-2.0.15 coverage-4.5.1 pytest-cov-2.5.1 saxpy-1.0.0.dev154

2.0 Time series to SAX conversion

To convert a time series of an arbitrary length to SAX we need to define the alphabet cuts. Saxpy retrieves cuts for a normal alphabet (we use size 3 here) via cuts_for_asize function:

from saxpy.alphabet import cuts_for_asize
cuts_for_asize(3)

which yields an array:

array([      -inf, -0.4307273,  0.4307273])

To convert a time series to letters with SAX we use ts_to_string function but not forgetting to z-Normalize the input time series:

from saxpy.znorm import znorm
from saxpy.sax import ts_to_string
ts_to_string(znorm(np.array([-2, 0, 2, 0, -1])), cuts_for_asize(3))

this produces a string:

'abcba'

3.0 API usage

There two classes implementing end-to-end workflow for SAX. These are TSProcessor (implements time series-related functions) and SAXProcessor (implements the discretization). Below are typical use scenarios:

3.1 Discretizing time-series by chunking:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization
String str = sp.ts2saxByChunking(ts, paaSize, na.getCuts(alphabetSize), nThreshold);

// print the output
System.out.println(str);

3.2 Discretizing time-series via sliding window:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization
SAXRecords res = sp.ts2saxViaWindow(ts, slidingWindowSize, paaSize, 
	na.getCuts(alphabetSize), nrStrategy, nThreshold);

// print the output
Set<Integer> index = res.getIndexes();
for (Integer idx : index) {
	System.out.println(idx + ", " + String.valueOf(res.getByIndex(idx).getPayload()));
}

3.3 Multi-threaded discretization via sliding window:

// instantiate classes
NormalAlphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// read the input file
double[] ts = TSProcessor.readFileColumn(dataFName, 0, 0);

// perform the discretization using 8 threads
ParallelSAXImplementation ps = new ParallelSAXImplementation();
SAXRecords res = ps.process(ts, 8, slidingWindowSize, paaSize, alphabetSize, 
	nrStrategy, nThreshold);

// print the output
Set<Integer> index = res.getIndexes();
for (Integer idx : index) {
	System.out.println(idx + ", " + String.valueOf(res.getByIndex(idx).getPayload()));
}

3.4 Time series motif (recurrent pattern) discovery

Class SAXRecords implements a method for getting the most frequent SAX words:

    // read the data
double[] series = TSProcessor.readFileColumn(DATA_FNAME, 0, 0);

// instantiate classes
Alphabet na = new NormalAlphabet();
SAXProcessor sp = new SAXProcessor();

// perform discretization
saxData = sp.ts2saxViaWindow(series, WIN_SIZE, PAA_SIZE, na.getCuts(ALPHABET_SIZE),
    		NR_STRATEGY, NORM_THRESHOLD);
    		
    // get the list of 10 most frequent SAX words
ArrayList<SAXRecord> motifs = saxData.getMotifs(10);
SAXRecord topMotif = motifs.get(0);
    
    // print motifs
System.out.println("top motif " + String.valueOf(topMotif.getPayload()) + " seen " + 
	   		topMotif.getIndexes().size() + " times.");

3.5 Time series anomaly detection using brute-force search

The BruteForceDiscordImplementation class implements a brute-force search for discords, which is intended to be used as a reference in tests (HOTSAX and NONE yield exactly the same discords).

discordsBruteForce = BruteForceDiscordImplementation.series2BruteForceDiscords(series, 
   WIN_SIZE, DISCORDS_TO_TEST, new LargeWindowAlgorithm());
    
    for (DiscordRecord d : discordsBruteForce) {
       System.out.println("brute force discord " + d.toString());
    }

3.6 Time series anomaly (discord) discovery using HOTSAX

The HOTSAXImplementation class implements a HOTSAX algorithm for time series discord discovery:

  discordsHOTSAX = HOTSAXImplementation.series2Discords(series, DISCORDS_TO_TEST, WIN_SIZE,
      PAA_SIZE, ALPHABET_SIZE, STRATEGY, NORM_THRESHOLD);
      
  for (DiscordRecord d : discordsHOTSAX) {
    System.out.println("hotsax hash discord " + d.toString());
  }

Note, that the "proper" strategy to use with HOTSAX is NumerosityReductionStrategy.NONE but you may try others in order to speed-up the search, exactness however, is not guaranteed.

The library source code has examples (tests) for using these here and here.

Made with Aloha!