lambdai — Untyped Lambda Calculus Interpreter

This application tries to reduce arbitrary lambda terms to their normal form using either normal oder applicative order. δ- as well as β-reductions are supported. The trace of the whole reduction is shown to the user.

This application is designed for educational purposes.

Installation

This package uses Cabal.[fn:1] Therefore you can use the following commands in the root of the source tree.

cabal configure
cabal build
cabal install

Usage

Invoke by the use of cabal run in the root of the source tree or lambdai if the package is installed.

Evaluation Order

This package implements two evaluation orders: normal order (outermost left first) and applicative order (innermost left first). Of which the default evaluation order is the normal order.

The evaluation order can be changed by using the :evalOrder directive.

Change to normal order:

:render normal

Change to applicative order:

:render applicative

Argument Passing

Two argument passing strategies are supported. If arguments are passed by value they are evaluated before the function is applied to them. If they’re passed by label they aren’t evaluated before application.

In this package this is implemented so that the arguments are reduced only by the use of β-reductions until no further possible, before the function is applied to them, if pass by value is selected.

The default argument passing strategy is pass by name.

Change to pass by name:

:passBy name

Change to pass by value:

:passBy value

Output

The two different modes for rendering reduction traces are described below.

Terminal

Terminal (or command line) is the default output mode. To change the output mode to terminal use:

:render cl

LaTeX

When the LaTeX output mode is used, all traces are rendered as LaTeX code. To use the output in your document, you need to place it in a math environment. And include the amsmath and amssymb packages.

To change the output mode to LaTeX use:

:render latex

Example:

\documentclass{standalone}

\usepackage{amsmath}
\usepackage{amssymb}

\begin{document}

\begin{math}
  \begin{aligned}
        & \underline{square}\;(square\;5)                                                \\
    =\; & \underline{(\lambda x.*\;x\;x)\;(square\;5)}         & \quad \therefore \delta \\
    =\; & *\;(\underline{square}\;5)\;(square\;5)              & \quad \therefore \beta  \\
    =\; & *\;(\underline{(\lambda x.*\;x\;x)\;5})\;(square\;5) & \quad \therefore \delta \\
    =\; & *\;(*\;5\;5)\;(\underline{square}\;5)                & \quad \therefore \beta  \\
    =\; & *\;(*\;5\;5)\;(\underline{(\lambda x.*\;x\;x)\;5})   & \quad \therefore \delta \\
    =\; & *\;(*\;5\;5)\;(*\;5\;5)                              & \quad \therefore \beta  \\
  \end{aligned}
\end{math}

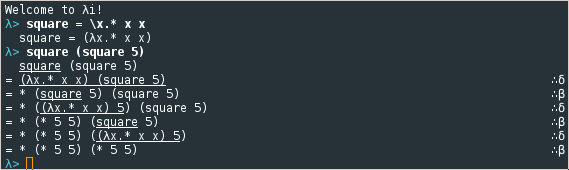
\end{document}

Example Session

Welcome to λi!
λ> square = \x.* x x
  square = (λx.* x x)
λ> square (square 5)
  square (square 5)
= (λx.* x x) (square 5)                                                       ∴δ
= * (square 5) (square 5)                                                     ∴β
= * ((λx.* x x) 5) (square 5)                                                 ∴δ
= * (* 5 5) (square 5)                                                        ∴β
= * (* 5 5) ((λx.* x x) 5)                                                    ∴δ
= * (* 5 5) (* 5 5)                                                           ∴β
λ> 

Footnotes

[fn:1] https://www.haskell.org/cabal/