lambdai — Untyped Lambda Calculus Interpreter

This application tries to reduce arbitrary lambda terms to their normal form using either normal oder applicative order. δ- as well as β-reductions are supported. The trace of the whole reduction is shown to the user.

This application is designed for educational purposes.

Installation

This package uses Stack as build system. Therefore you can use the following command in the root of the source tree.

stack install

Usage

Invoke by the use of stack exec lambdai or stack exec lambdaid respectively in the root of the source tree or lambdai ord lambdaid respectively if the package is installed.

λi Daemon

The λi daemon (lambdaid) runs on port 3000 by default. Each request is handled as a separate λi session. The reductions performed on the server are limited to 3000. The output is rendered using MathJax.

Evaluation Strategies

λi supports the following four distinct evaluation strategies out of the box. All four have in common, that they always prefer β-reductions over δ-reductions. This means δ-reductions are only performed if no further β-reductions are possible, given a certain evaluation order. When using pass by name or pass by value, terms are only reduced until they are in HNF (head normal form). Therefore even if β-reductions inside a lambda abstraction are still possible, δ-reductions outside the outermost lambda abstraction are performed, because these evaluation strategies don’t allow any furhter β-reductions in such a term.

normal order

Does reductions on leftmost outermost subterms first. This strategy always finds a NF (normal form) if it exists.

applicative order

Does reductions on the leftmost innermost subterms first. This strategy may not find a NF even if it exists, but requires fewer steps than normal order evaluation in certain situations.

pass by name

The same as normal order, except that no reductions inside of lambda abstractions are performed. This always finds a HNF if it exists.

pass by value

The same as applicative order, except that no reductions inside of lambda abstractions are performed. This doesn’t always find a HNF if it exists.

In lambdai one may use the :strategy <strategy> directive to change the evaluation strategy interactively.

<strategy> ::= normalOrder | applicativeOrder | callByName |
 		    callByValue

In lambdaid the evaluation strategy may be changed using the respective selection box.

Evaluation Step Limit

The maximum of reductions to be performed by λi may be limited in an interactive command line session and are always limited when using the web interface.

If the maximum of reductions is set to zero, an infinite amount of reductions are performed.

On the command line the :maxSteps <unsigned integer> directive may be used to change this limit.

Output (command line)

The two different modes for rendering reduction traces are described below.

Terminal

Terminal (or command line) is the default output mode. To change the output mode to command line use:

:render cl

LaTeX

When the LaTeX output mode is used, all traces are rendered as LaTeX code. To use the output in your document, you need to place it in a math environment. And include the amsmath and amssymb packages.

To change the output mode to LaTeX use:

:render latex

Example:

\documentclass{standalone}

\usepackage{amsmath}
\usepackage{amssymb}

\begin{document}

\begin{math}
  \begin{aligned}
        & \underline{square}\;(square\;5)                                                \\
    =\; & \underline{(\lambda x.*\;x\;x)\;(square\;5)}         & \quad \therefore \delta \\
    =\; & *\;(\underline{square}\;5)\;(square\;5)              & \quad \therefore \beta  \\
    =\; & *\;(\underline{(\lambda x.*\;x\;x)\;5})\;(square\;5) & \quad \therefore \delta \\
    =\; & *\;(*\;5\;5)\;(\underline{square}\;5)                & \quad \therefore \beta  \\
    =\; & *\;(*\;5\;5)\;(\underline{(\lambda x.*\;x\;x)\;5})   & \quad \therefore \delta \\
    =\; & *\;(*\;5\;5)\;(*\;5\;5)                              & \quad \therefore \beta  \\
  \end{aligned}
\end{math}

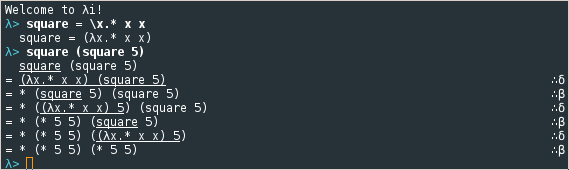
\end{document}

Example Session

Welcome to λi!
λ> square = \x.* x x
  square = (λx.* x x)
λ> square (square 5)
  square (square 5)
= (λx.* x x) (square 5)                                                       ∴δ
= * (square 5) (square 5)                                                     ∴β
= * ((λx.* x x) 5) (square 5)                                                 ∴δ
= * (* 5 5) (square 5)                                                        ∴β
= * (* 5 5) ((λx.* x x) 5)                                                    ∴δ
= * (* 5 5) (* 5 5)                                                           ∴β
λ>