- 数据结构与算法
数据分为数值性数据和非数值数据,其基本单位是数据元素,是计算机处理或访问的基本单位;
一个数据元素可以由若干数据项组成,数据项又称属性,字段,域,分为初等项(不可分割)和组合项;
结构:数据元素之间的关系;
数据结构是由与特定问题相关的某一数据元素的集合(对象)(Data)和该集合中数据元素之间的关系(Relationship)组成的;分为静态数据结构和动态数据结构,舍弃了实际的物理背景,是通用型的定义;
数据结构={D,R}
数据对象:狭义:具有一定关系的相同性质的数据元素的集合;广义:由数据抽象和处理数据构成的封装体
数据类型:一个值的集合和定义在这个值集合上的一组操作的总称,分为内置数据类型(亦称基本数据类型或原子类型,可直接使用)和构造数据类型(由不同成分的内置数据类型子结构按照一定的规则组成,是用编程语言描述的数据结构的存储映像),是数据结构的实例化;数据类型再实例化得到具体变量,如类与对象;
抽象数据类型ADT(Abstract Data Type):
抽象的本质就是抽取反映问题本质的东西,忽略非本质的细节;
特性:使用与实现相分离,数据封装与信息隐蔽;
在C++,java中用类描述。C中一般不使用ADT,数据和结构是分开的。
数据结构:
三要素:逻辑结构,存储结构,数据运算。
一,分解和抽象:1,数据分解划分出数据的层次,再抽象得到数据的逻辑结构;2,处理分解划分成各种功能,再通过抽象得到算法的定义。这是一个从具体(具体问题)到抽象(数据结构与算法)的过程;进一步通过对实现细节的进一步考虑得到存储结构和实现运算,从而完成程序设计的任务,实现从数据结构到具体实现。
二,逻辑结构和存储结构
数据的逻辑结构根据问题所要实现的功能建立(不考虑具体实现),存储结构根据问题所要的需求(响应速度,处理时间,等)来实现数据的逻辑结构。(数据结构一般指的就是逻辑结构,逻辑结构相同,即使存储结构不同也是相同的逻辑结构);
逻辑结构的分类:
线性结构 ,树形结构 ,图结构, 集合结构。
线性结构:元素之间的关系是一对一的,如线性表,向量,栈,队列,优先队列,字典等;
非线性结构:每个数据结构可能与零个或多个其他数据元素发生联系,分为树结构(一对多)和图结构(多对多)。 如多维数组和广义表等;
集合结构的实现往往采用其他逻辑结构的存储表示。
数据结构的存储结构:
存取结构根据存取方法的不同分为三类:
1,直接存取结构(向量,多维数组,散列表);
2,顺序存取结构(各种链表,图的邻接表);
3,索引存取结构(线性索引,多叉查找树);
常用的四种存储结构
1,顺序存储:元素之间的逻辑关系由存储单元的邻接位置关系体现,由此得到顺序存储结构,借助一维数组描述;
2,链接存储:元素之间的逻辑关系由附加的链接指针指示,由此得到链表存储结构,借助指针类型描述;
3,索引存储:在存储元素信息的同时还建立索引表,其中每一项称为索引项(包括关键码和地址),按针对一个元素还是一组元素分为稠密索引和稀疏索引;按是一层还是多层分为线性索引和多级索引;
4,散列存储:根据元素的关键码通过一个函数计算得到元素的存储地址。
前两种在内存中,也是基本的两种物理存储结构。后两个在外存中。/
选择存储结构的要素有<1>访问频率,<2>修改频率,<3>安全保密;
定义在数据结构上的操作:
1,创建;2,销毁;3,查找;4,插入;5,删除;6,排序。
好的数据结构:可以通过某种“线性化”规则被转化为线性结构,通常对应好的算法;
计算机本质上只能按照逻辑顺序处理指令和内存单元,例如图,树的遍历查找需要线性化。
大多数运算符结合方向是“自左至右”,即:先左后右,也叫“左结合性”,例如 a-b + c,表达式中有-和+两种运算符,且优先级相同,按先左后右结合方向,先围绕减号结合,执行a-b的运算,再围绕加号结合,完成运算(a-b) + c。除了左结合性外,C 语言有三类运算符的结合方向是从右至左,也叫“右结合性”,即:单目运算符(只有一个操作数)、条件运算符、以及赋值运算符。着重强调一点,无论是左结合性,还是右结合性,是针对两个相邻的优先级相同的运行符而言(不是表达中的运算对象),运算符是决定左右的基准点,先以前面的运算符(即位置上处于左边的运算符)构造运算,就是左结合,反之,就是右结合。
条件运算符嵌套时必要时用优先级最高的括号分隔
函数参数自右向左进栈,要考虑右边参数对左边的影响。
i++ 与 ++i 的主要区别有两个: 1、 i++ 返回原来的值,++i 返回加1后的值。 2、 i++ 不能作为左值,而++i 可以。
i=1; j=i+++i++;先执行两个i++,返回值分别为1和2;i自增两次,所以j=i=3;
只能用于左值,例如(num+1)--是错误的
char*==string.c_str();
sprintf(s, "%d", x);将%d形式的x以字符串形式放在s里,并自动添加结尾
int->string:
std::to_string(int)
std::to_string(long)
std::to_string(long long)
std::to_string(float)
std::to_string(double)
std::to_string(long double)
还支持各类unsigned,基本上主流数值类型都能无脑转换
string->int:
//#include<cstdlib>
std::stoi
std::stol
std::stoll
//看名字就知道对应为int,long,long long
int stoi (const string& str, size_t* idx = 0, int base = 10)
int x=stoi(s);
stoi(string.c_str(),idx,base);
//比atoi安全
//idx是一个指针,该指针指向一个size_t类型的对象
//传入指针地址后,该对象的值会被修改为string中数值后的第一个字符所在位置
//例如stoi("123abcd",&p),返回的p指向a所在
进制是输入数字的进制;不常用。
不用区分行列遍历
void Print(int *p,int n)//或int p[];
{
for(int i=0;i<n;i++)//存储在一块连续的区域
printf("%d ",p[i]);
printf("\n");
}
int main()
{
int s[2][3]={1,2,3,4,5,6};
Print((int*)s,6);//(int*)s==s[0];
return 0;
}
void Print(int **p)
{
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < 3; j++)
printf("%d ", *(( int* )p+ 2*i + j));//编译器寻址方式,根据二级指针不能自动寻址
}
printf("\n");
}
int main()
{
int s[2][3] = {1, 2, 3, 4, 5, 6};
Print((int **)s);
return 0;
}
二维数组名的类型是type (*)[n];是一个数组指针,可强制转换成type**和type*,地址是一样的
常用
int s[][n];n不能为空。一维数组也建议用int s[];较直观,便于与其他的指针区分。
int **s = (int **)malloc(2 * sizeof(int *));
for (int i = 0; i < 2; i++)
s[i] = (int *)malloc(3 * sizeof(int));
for(int j = 0; j <2;j++)
{
for(int k = 0;k<3;k++)
s[j][k]=1;
}
for(int j = 0; j <2;j++)//逐层由内向外释放
free(s[j]);
free(s);
int *s[2];
for (int i = 0; i < 2; i++)
s[i] = (int *)malloc(3 * sizeof(int));
for(int j = 0; j <2;j++)
{
for(int k = 0;k<3;k++)
s[j][k]=1;
}
for(int j = 0; j <2;j++)//不用也不能释放s,它不是动态分配的
free(s[j]); void* realloc(void* ptr, unsigned newsize);
//对malloc申请的内存进行大小的调整.
void* calloc(size_t numElements, size_t sizeOfElement);
//初始化分配的内存,设置为0
void *memset(void *s, int ch, size_t n);
//将s中当前位置后面的n个字节 (typedef unsigned int size_t )用 ch 替换并返回 s 。
//memset函数按字节对内存块进行初始化,所以不能用它将int数组初始化为0和-1之外的其他值(除非该值高字节和低字节相同)。calloc相当于malloc加memset;
函数需要返回字符串时不能返回局部变量,只能返回形参中的字符串或用动态分配的空间,一般用calloc(不用担心结尾是否为0)
如果A为假,则A&&B短路,如果A为真,则A||B短路,不再判断B。
应用:对于A||B如果A真时B可能溢出则A必须在前;
避免短路时可用按位操作,注意只能是bool之间比较
1,*(type(*)[len])arrname;强制转换为数组指针(它的最本质类型),再取值。
2,*(arrname)@len;用这个简单。
void delchar( char *str, char c )//删除单个位置的元素时用顺移较为简单
{
int i=0,j=0;//
while(str[i])//用j的话需要在结尾加\0
{
if(str[j]!=c)
str[i++]=str[j];
j++;
}
}
while (i<L.num)//线性表删除特定元素
{
if (L.data[i] != x)
{
L.data[j++] = L.data[i];
}
i++;
}
L.num =j;
for (i = 1; i < L.num; i++)//无序线性表删除重复元素,有序的与有序区的结尾元素进行比较即可
{
for (j = 0; j <= k; j++)//k:border of non-repreting region
{
if (L.data[i] == L.data[j])
break;
}
if (j > k)
L.data[++k] = L.data[i];
}
L.num = k + 1;
while(i<A.num&&j<B.num)//求有序表共有元素
{
if(A.data[i]<B.data[j])
i++;//跳过小的元素
else if(A.data[i]>B.data[j])
j++;
else same=A.data[i];
}void ten2two(int n)
{
if(n>0)
{
ten2two(n/2);
printf("%d",n%2); //递归为逆序输出,故先写调用函数,后写printf
}
else
return;int convert(int n)
{
if(n==0||n==1)
return n;
else
return n%10+2*convert(n/10);
}将2到36进制数转换为10进制
int Atoi(string s,int radix) //s是给定的radix进制字符串
{
int ans=0;
for(int i=0;i<s.size();i++)
{
char t=s[i];
if(t>='0'&&t<='9') ans=ans*radix+t-'0';
else ans=ans*radix+t-'a'+10;
}
return ans;
}
//利用库函数
string s = "bacppp";
char *stop;
cout << strtol(s.c_str(), &stop, 16) <<endl<<stop<< endl;//stop是非法部分,注意引用符号
//返回值类型是long
2988
ppp
//利用栈
void SysConvert( string s, int init, int k)
{
char *t;
long num = strtol(s.c_str(), &t, init);
SeqStack(S);
InitStack(S,int(log(num)/log(k))+1);
while(num)
{
Push(S,num%k);
num/=k;
}
PrintStack(S);
}#include<stdio.h>
#include<math.h>
int main(){
printf("%f\n",log(10)); //以e为底的对数函数
printf("%f\n",log10(100)); //以10为底的对数函数
printf("%f\n",log(8)/log(2)); //计算log_2^8,运用换底公式
printf("%f\n",exp(1)); //计算自然常数e
return 0;
} for(int j=0,index;j<i-1;j++)
{
index=j;
for(int k=j+1;k<i-1;k++)
{
if(strlen(s[k])<strlen(s[index]))
index=k;
}
printf("%s ",s[index]);//如果只是要输出将最小的依次输出然后把最小值替换即可,不用交换
strcpy(s[index],s[j]);
}结构体是一种类,拷贝概念上可近似看待
浅拷贝:拷贝过程中是按字节复制的,对于指针型成员变量只复制指针本身,而不复制指针所指向的目标。 值传递能保证值不变,但不能保证值上的值不变。函数传参时默认拷贝函数就是浅拷贝。 手动实现可以直接等或者用memcpy
memcpy(&CpA,&A,sizeof(struct SeqList));
另一个mem函数:void *memset(void *str, char c, size_t n) 复制字符 c(一个无符号字符)到参数 str 所指向的字符串的前 n 个字符。 memset(str,'$',7);
深拷贝:自定义拷贝函数,以实现完全复制
void DeepCopy(SeqList &CpTemp, SeqList A)
{
CpTemp.num = A.num;
CpTemp.data = new DataType[Length];
for (int i = 0; i < A.num; i++)
{
CpTemp.data[i] = A.data[i];
}
}struct stu
{
int i;
char c;
char* p;
stu& operator=( const stu& stuTmp)//显式定义拷贝构造函数
{
i = stuTmp.i;//i==this->i;两侧能区分时可以省略
c = stuTmp.c;
p = new char(strlen(stuTmp.p) + 1);
strcpy(p, stuTmp.p);
return *this;返回拷贝的结构体
};
};
s2 = s1;当以拷贝的方式初始化一个对象时,会调用拷贝构造函数;当给一个对象赋值时,会调用重载过的赋值运算符
相当于s2.operator(s1);operator=() 的返回值类型为引用,这样不但能够避免在返回数据时调用拷贝构造函数,还能够达到连续赋值的目的
从X到Y,有Y-X+1个数,所以要产生从X到Y的数,只需要这样写: k=rand()%(Y-X+1)+X;
每次获取前运行srand(time(NULL));改变随机数计算函数初值,在time.h下。
一字节(byte)等于八位(bit);
整数取值范围:$\overbrace{100000....000}^{31}=-2^{31}$ 补码是源码除符号位外取反加一,逆推原码也是这样或者减一取反。$\overbrace{01111111111111111}^{32} =2^31-1$,具体值用pow表达式或者用确切值。
C:stdlib.h
void qsort(
void *base,
size_t number,
size_t width,//Element size in bytes.
int (__cdecl *compare )(const void *, const void *)//qsort calls the compare routine one or more times during the sort, and passes pointers to two array elements on each call. If compare indicates two elements are the same, their order in the resulting sorted array is unspecified.
);切记比较函数的参数类型是const void *
| Compare function return value | Description |
|---|---|
| < 0 | elem1 less than elem2 |
| 0 | elem1 equivalent to elem2 |
| > 0 | elem1 greater than elem2 |
小于时返回0也行,即要升序时用return elem1>elem2; The array is sorted in increasing order, as defined by the comparison function. To sort an array in decreasing order, reverse the sense of "greater than" and "less than" in the comparison function.
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>//极限:里面有INT_MIN,INT_MAX;
/*#define INT_MAX 2147483647
#define INT_MIN (-INT_MAX - 1),是一个符号而不是实际存在的数
INT_MAX + 1 = INT_MIN
INT_MIN - 1 = INT_MAX
abs(INT_MIN) = INT_MIN<0
*/
//快排整形
int compare_ints(const void* a, const void* b)
{
int arg1 = *(const int*)a;
int arg2 = *(const int*)b;
if (arg1 < arg2) return -1;
if (arg1 > arg2) return 1;
return 0;
// return (arg1 > arg2) - (arg1 < arg2); // possible shortcut,注意这种写法
// return arg1 - arg2; // erroneous shortcut (fails if INT_MIN is present)必须在整形范围内
}
int main(void)
{
int ints[] = { -2, 99, 0 ,-743, 2, INT_MIN, 4 };
int size = sizeof ints / sizeof *ints;//*ints=ints[0];注意学习
qsort(ints, size, sizeof(int), compare_ints);
for (int i = 0; i < size; i++) {
printf("%d ", ints[i]);
}
printf("\n");
}
//快排字符串
// crt_qsort.c
// arguments: every good boy deserves favor
/* This program reads the command-line
* parameters and uses qsort to sort them. It
* then displays the sorted arguments.
*/
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
int compare( const void *arg1, const void *arg2 );\\把程序本身的名字赋值给argv[0],接着,把后面的第一个字符串赋给argv[1]
int main( int argc, char **argv )
{
int i;
/* Eliminate argv[0] from sort: */
argv++;//注意学习
argc--;
/* Sort remaining args using Quicksort algorithm: */
qsort( (void *)argv, (size_t)argc, sizeof( char * ), compare );//被排元素是字符串指针
//前两个类型转换可以省略
/* Output sorted list: */
for( i = 0; i < argc; ++i )
printf( " %s", argv[i] );
printf( "\n" );
}
int compare( const void *arg1, const void *arg2 )
{
/* Compare all of both strings: */
return _stricmp( * ( char** ) arg1, * ( char** ) arg2 );//*(**)将一般指针转化为字符串指针
//stricmp相当于_stricmp的alias,是不区分大小写的strcmp,windows独有,linux下用strcasecmp替代
}cpp:algorithm
void sort( RandomIt first, RandomIt last );
sort(a,a+10);//
void sort( RandomIt first, RandomIt last, Compare comp );
sort(a,a+10,compare);
sort(a,a+10,less<int>());
sort(a,a+10,greater<int>());
bool compare(int a,int b)
{
return a>b;//降序
}
std::array<int, 10> ints = {5, 7, 4, 2, 8, 6, 1, 9, 0, 3};
sort(ints.begin(), ints.end(), compare_ints);
for (int i = 0; i < ints.size(); i++)
{
printf("%d ", ints[i]);
}
comp:For all a, comp(a,a)==false
If comp(a,b)==true then comp(b,a)==false
if comp(a,b)==true and comp(b,c)==true then comp(a,c)==true
c的comp参数为(常无类型)指针,返回值为int(不支持bool),c++的comp参数为元素本身,返回值为bool。 c return a>b是升序,c++的是降序(less的在前);
**快排的时间复杂度为O(nlogn);
算法:一个有穷的指令集。
1,有输入:可以通过输入语句由外部显式提供,也可以由赋值或定值语句隐式提供,即 “0个输入“ 情况; 2,有输出; 3,确定性:每一步都确切,无歧义的定义,对于一组确定的输入对应一条确定的路径运算,如果会因系统状态而导致结果不一致,则只要对于每个系统状态有确定的处理手段就不影响确定性,没赋初值导致的结果不同没有对应不同状态的处理,违反确定性。 4,有穷性:初值导致算法不收敛的与算法本身无关,不违反有穷性; 5,可行性:每一条运算都足够基本(可以用基本操作或调用已实现的基本算法),都能精确执行,但并不一定都与机器指令有直接关系,并能在常数时间内完成。
基本设计步骤:理解需求->设计思路->算法框架->程序实现;
算法与程序的关系: (1)算法在描述上一般使用半形式化的语言,而程序是用形式化的计算机语言描述的。 (2) 程序是计算机指令的有序集合。 (3)程序并不都满足算法所要求的特征,例如操作系统,是一个在无限循环中执行的程序,因而不是一个算法。 (4)一个算法可以用不同的编程语言编写出不同的程序。 (5)算法是解决问题的步骤;程序是算法的代码实现。 (6)算法要依靠程序来完成功能;程序需要算法作为灵魂。 (7)程序=算法+数据结构。
算法设计基本方法:
1,穷举法(枚举法):<1>按规则列举,<2>盲目列举,并检查之前的列举是否重复;
2,迭代法(反复法):iteration:不断用原值得到的新值代替原值,直到得到满意的解 ,新值与原值之间的关系用迭代公式表示,主要用于很难用或无法用解析法求解的计算问题,例如区间折半法求方程的根,也用来遍历表树图等数据结构。
3,递推法:递归的递推求解使用递归法,自顶向下,非递归的递推求解使用迭代法,自底向上;
4,递归法:包括自身的数据对象和调用本身的过程是递归的;递归从问题规模为n的场合开始,通过递归降低问题规模,直到递归出口,再倒推回来得到最初的值;递推是从已知条件出发;一般一个递推算法总可以转化为递归算法;例如二分法求根和求Fibonacci数两种方式的转换。但递归法不仅仅用于递推的实现(还有数据结构如链表,树图等的建立等等)。
递归是算法设计的基本技术,是降低分析设计难度提高程序设计效率的重要手段和工具;迭代具有更高的时空效率。
穷举过程中被穷举对象可能需要其他方法求解,各种方法是配合使用的。
算法度量
算法的评价标准: 1,正确性; 2,健壮性:在不正确输入条件下能自我保护,包括自动检错,报错,与用户对话来纠错; 3,可读性;变量名,函数名要有实际意义,必须加入注释; 4,高效性:主要指算法的时间代价和空间代价; 5,简单性:主要用环路复杂度度量,等于程序中判断语句和子程序调用总数加一,软件工程要求不能超过10;
算法分析的主要方法:事后估算法(插入测量时间语句来估算)和事前统计法(通过对问题规模,执行频度,时间,空间复杂度的进行估算。主要目的是分析算法的效率以求改进。主要方面是时间性能和空间性能。
clock_t start_time, end_time;给两个变量赋给当时时间,它们的差就是它们之间程序的运行时间
clock_t是长整形。
用clock()(精确到豪秒)或者time(NULL/0)(精确到秒)
用time直接作差即可,用clock的需要使用表达式(double)(end_time-start_time)/CLOCK_PER_SEC(每秒钟clock的增量,linux下为1000000,window下为1000);
特别的sleep(x)(unisted.h)下会使linux下的clock暂停(它返回的是CPU耗费在本程序上的时间。也就是说,途中sleep的话,由于CPU资源被释放,那段时间将不被计算在内。)等待输入时clock也会暂停,带有sleep的程序运行时间精度要求不高时只能用time;windows不会;
window下sleep(n)单位是ms,linux下单位是s;linux下还有usleep(n),单位是um。里面乘以1000就等同于window下的sleep。
精确计算运行时间
#include <sys/time.h>
struct timeval start_time,end_time;
int main()
{
gettimeofday(&start_time,NULL);
/*
代码块
*/
gettimeofday(&end_time,NULL);
printf("%lf",(end_time.tv_sec-start_time.tv_sec)+(double)(end_time.tv_usec-start_time.tv_usec)/CLOCKS_PER_SEC);
return 0;
}
/*
gettimeofday()会把目前的时间用tv 结构体返回,当地时区的信息则放到tz所指的结构中。
一般情况下 ,我们并不需要时区信息,所以第二个参数通常为空。
timeStart.tv_sec 这个就是秒为单位的时间戳。(double)
timeStart.tv_usec 这是当前秒中的毫秒数。(int,需要除以CLOCK_PER_SEC并转为double);
*/C++利用chrono库也可以测量时间,可以使用更适合测量程运行时间的steady_clock()来测量。
#include <iostream>
#include <chrono>
struct Timer
{
std::chrono::time_point<std::chrono::high_resolution_clock> start, end;
//hign_resolution_clock是steady_clock的进阶版(系统所能提供的最精确),同时steady_clock(表在裁判手里,不能修改)相比于system_clock(表在系统手里,会被各种行为修改)更适合计时
std::chrono::duration<float> duration;
Timer()
{
start = std::chrono::high_resolution_clock::now();//nm clock
}
~Timer()
{
end = std::chrono::high_resolution_clock::now();
duration = end - start;
std::cout << "Timer took" << duration.count() * 1000<< "ms" << std::endl;
//float型的duration是mircoseconds类型,乘1000是毫秒
}
};
//在函数前面定义一个Timer对象即可计时
//手动计时
#include<thread>
#include <chrono>
#include<iostream>
using namespace std::chrono;
using namespace std::literals::chrono_literals;//为sleep部分提供命名空间
auto begin =high_resolution_clock::now();
this_thread::sleep_for(1s);
auto end = high_resolution_clock::now();
auto duration = end - begin;//auto推断得到的是 nanoseconds
double ms=(double)duration.count()/CLOCKS_PER_SEC;
//auto deration =duration_cast<milliseconds>(end-begin);//强制转换为ms,精度不如上面的方式
cout << duration.count() <<"ms"<< endl;
cout<<ms<<"ms"<<endl;算法的计算量的大小称为算法的复杂性。
问题规模从问题的描述中找到:例如在n个学生中查找和求解n阶线性方程组的问题规模都是n;
时间复杂度T(n):当问题的规模从1增加到n时,解决问题的算法所耗费的时间也由1增加到T(n);
空间复杂度S(n):空间由1到S(n);
两种度量都是问题规模n的函数,单位都是1,即单位时间(ont time unit)和单位空间都是1(ont space unit);
时间复杂度度量的计算
算法的执行频度=每条语句的执行次数(频度)x该语句执行时间(每一条基本语句执行时间视为单位时间1,语句执行时间等于语句中基本运算语句数)=算法中所有运算语句执行频度的总和;
for循环控制语句的执行次数为n+1,;单位执行时间(一次执行所需语句数)为2(不包括内部),执行频度(总次数)为2(n+1)(共执行n+1次表达式2,1次表达式1,n次表达式3),循环体执行次数是n;
运算赋值语句是一个基本运算语句(加减乘除,转移,存取以及他们的复合),如a=b+c,return b+c,执行频度都是1;定义语句不是运算语句;
递归算法的执行频度可通过写出T(n)的递推形式来计算;例如T(n)=2,n<=0(if判断和return);T(n)=2+T(n-1);n>0;(比上次多两次执行(if和return加和,调用函数以及return的执行次数和加和合并了,还是1);
空间复杂度度量指算法所需附加存储空间,包括固定部分和可变部分(与问题规模有关);
阶乘的非递归实现中,只用了一个整数存放连乘结果,附加空间数为1,空间复杂度也为1;
递归的空间复杂度=每次递归所要的辅助空间x递归深度
阶乘的递归i实现中每一层递归都需要三个栈空间来存放形式参数,返回值以及返回地址(一旦函数调用完成,程序应该知道返回的位置,即函数调用之前的点)
递归深度是n,所以所需的栈空间是3n,空间复杂度为3n;
动态分配所涉及的空间复杂度 等于malloc的空间减去free的空间;
执行频度不能确切地反映运行时间,所以用其来比较两个程序结果不一定有价值,所以只需给出算法执行频度的数量级即可达到分析的目的。
大O表示:当且仅当存在正整数c和n_0,使得T(n)<=cxf(n)对所有的n>=n_0成立,则称该算法的时间增长率在O(f(n))中,记为T(n)=O(f(n)).
算法时间复杂度T(n)增长的上限为f(n);Never to underestimate the runing time of the program.
O 函数的渐近上界 upper bound Ω 函数的渐近下界 lower dound Θ 函数的准确界
Θ(f(n))=T(n):存在正常数c1,c2和n0,使对所有的n⩾n0,有0⩽c1f(n)⩽T(n)⩽c2f(n) f(n)=2n^2+n,T(n)=n^2;(同阶)同速
O(f(n))=T(n): 存在正常数c和n0,使对所有n⩾n0,有0⩽T(n)⩽cf(n) f(n)=n^2;T(n)=2n^2+n; f(n)_rate>=T(n)_rate
Ω(f(n))=T(n): 存在正常数c和n0,使对所有n ⩾ n0,有0⩽cf(n)⩽T(n) f(n)=n^2,T(n)=2n^2+n;f(n)_rate<=T(n)_rate
o(f(n))=T(n): 对任意正常数c,存在常数n0>0,使对所有的n⩾n0,有0⩽T(n)⩽cf(n) T(n)=O(f(n))&&T(n)!=Ω(f(n));f(n)=2n^2+n;T(n)=2n;
f(n)_rate>T(n)_rate
lim(T(n)/f(n))=lim(T'(n)/f'(n))(n->inf):1,==c:Θ(f(n))=T(n);2,->inf:o(T(n))=f(n);3,==0;o(f(n))=T(n);
Thus T(n)=n^2=O(n^2)=O(n^3),the first option is the best answer.
一般情况下O就是指Θ,前者范围更广所以一般用前者表示。
If T(N)is a polynomial(/ˌpɑːliˈnoʊmiəl/ 多项式) of degree k(equal to k-order),then T(N)= Θ(N^k);
Lower-order terms can generally be ignored,and the constants can be throw away.
If T1(n) = O(F(N)) and T2(N) = O(g(N)),then (a),T1(N)+T2(N) = max{O(f(N)),O(g(N))} (b),T1(N)*T2(N) = O(f(N)*g(N)).
When n is sufficiently large, the growth of various functions has the following relationship:
c < log2n < (log2n)^k<n < nlog n < n^2 < n^3 < 2^n < 3^n < n! <n^n
Constant logarithmic Linear Quadratic Cubic Exponential factorial /ˌekspəˈnenʃl/ The logarithms grow very slowly.
the rate of logarithm slower than power slower than exponient,there is no power function between n and nlogn.
such as :
O(log2n)可以简记为O(logn);由换底公式知不同底数的对数阶只差了常数倍,n(log2n)也满足.
for loop statement:The total running time of a statement(语句) inside a group of nested loops(嵌套循环) is the running time of statement multiplied by the product(乘积) of the size of all the for loops;
if/else statement:time of test plus the lager of the running time of S1 and S2.
函数或语句嵌套的相乘,并列的取最大。
计算递归的时间复杂度时,简单的可以直接当作for循环来看,复杂的通过递推式计算,结束递归那一步的执行频度如果是c可以简化为1,递推式中的常数必须严格按其执行频度来,例如裴波那契数列递归式是T(n)=T(n-1)+T(n-2)+2(if和return那一句),n=1,2时看作1还是2无所谓。
图片:超链接的格式前加!
一个行内,两个行外;_下标,^上标 逻辑上的括号:{}
分数:\frac{}{}
方程组:\begin{cases} \\ \\ \\ \end{cases}
求和:\sum_{i=0}^k;
连乘:\prod_{i=0}^n
换行\\,空格\;
箭头\rightarrow
自适应括号\left( \right)
\sqrt{}
大于等于:\geq;
属于 \in
小于等于:\leq;
不等于:\neq;
$\lfloor x \rfloor$向下取整;
$\lceil x \rceil$向上取整
行内:一个\$,或**ctrlM**行外两个\$,
有两种省略号,\ldots 表示语文本底线对其的省略号,\cdots表示与文本中线对其的省略号。
\cap:∩ \bigcap \cup ∪ $
注意竖线与内容间的空格和标题与内容的分割线,不需要用$包围
| 名称 | 缩写 |
|---|---|
| JavaScript | js |
| Python | py |
| C++ | cpp |
| “:”:决定对齐方式 | |
| 题号 | 标题 |
| :--- | ---: |
| 1 | 两数之和 |
| 15 | 三数之和 |
| 262 | 行程和用户 |
{
int i,j,k,x=0,y=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
for(int k=1;k<=j;k++)
x=x+y;
}{
int func(int n)
{
int i=1,s=1;
while(s<n)
s+=++i;
return i
}
}
第一轮 :s=1+2;第二轮:s=1+2+3;第n轮:s=1+2+3+...+i;跳出循环时,函数执行次数i满足$\frac{n(n- 1)}{2}\geq n$;即
Find the maximum of subsequence(substring) sum in A[n]:{A0,A1,...An};
Algorithm 1
int MaxSubsequenceSum(const int A[],int N)
{
int ThisSum,Maxsum,i,j,k;
Maxsum=0;
for(i=0;i<N;i++)
for(j=i;j<N;j++)
{
ThisSum=0;
for(k=i;k<=j;k++)
ThisSum+=A[k];
if(ThisSum>Maxsum)
Maxsum=ThisSum;
}
return Maxsum;
}evaluated inside out(由内到外计算)
求内层变量和时外层的变量当常量对待。
时间复杂度为O(n^3);不需要精确计算时可以通过三层循环的次数都小于等于n得到结果;
Algorithm2:
int MaxSubsequenceSum(const int A[],int N)
{
int ThisSum,Maxsum,i,j,k;
Maxsum=0;
for(i=0;i<N;i++)
{
ThisSum=0;
for(j=i;j<N;j++)
{
ThisSum+=A[j];
if(ThisSum>Maxsum)
Maxsum=ThisSum;
}
}
return Maxsum;
}
clearly is O(n^2);Algorithm3:
#include <iostream>
int Max3(int a, int b, int c);
int MaxSubSum(const int A[], int Left, int Right);
int main()
{
int a[5] = {1, 3, -5, 0, -8};
printf("%d", MaxSubSum(a, 0, 4));
return 0;
}
int Max3(int a, int b, int c)
{
if (a > b)
return a;
else if (c > b)
return c;
else
return b;
}
int MaxSubSum(const int A[], int Left, int Ri ght)
{
int MaxLeftSum, MaxRightSum;
int MaxLeftBorderSum, MaxRightBorderSum;
int LeftBorderSum, RightBorderSum;
int Center, i;
if (Left == Right)//递归返回终点
if (A[Left] > 0)
return A[Left];
else
return 0;
Center = (Left + Right) / 2;
MaxLeftSum = MaxSubSum(A, Left, Center);//递归计算两边的最大子列和,分治思想体现。
MaxRightSum = MaxSubSum(A, Center + 1, Right);
MaxLeftBorderSum = 0;
LeftBorderSum = 0;
for (i = Center; i >= Left; i--)
{
LeftBorderSum += A[i];
if (LeftBorderSum > MaxLeftBorderSum)
MaxLeftBorderSum = LeftBorderSum;
}
MaxRightBorderSum = 0;
RightBorderSum = 0;
for (i = Center + 1; i <= Right; i++)
{
RightBorderSum += A[i];
if (RightBorderSum > MaxRightBorderSum)
MaxRightBorderSum = RightBorderSum;
}
return Max3(MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum);
// 最大值在这三个值里产生
}The algorithm uses a "divide-and-conqure"(分治) strategy.The idea is spit the problem into two roughly equal subproblems,which are the solved recursively.
An Algorithm isO(log(N))if it takes constant(O(1))time to cut the problem size by a fraction(which is usually 1/2).On the other hand,if constant time is required to merely reduce the problem by a constant amount(such as make the problem smaller by 1),then the algorithm isO(N).
Simple intuition obviates the need for a brute-force approach.
接收n个数据至少需要O(N)的复杂度,故O(logN)是针对对应函数而不是程序整体说的。
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题,1<k≤n,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
Algorithm4
int MaxSubsequenceSum(const int A[],int N)
{
int ThisSum,Maxsum,j;
ThisSum=MaxSum=0;Maxsum=0;
for(j=0;j<N;j++){
ThisSum+=A[j];
if(ThisSum>MaxSum)//ThisSum大于零时更新(段内回撤不大不影响本金,长期持有)
MaxSum= ThisSum;
else if(ThisSum<0)//小于零后对后面部分的增长没有作用(回撤过大,割肉跑路),断开重新计算下一段的最大和
ThisSum=0;
}
return Maxsum;
}
//A[N] has presorted(一次排序,永远方便,需要多次查找的都可以这样搞)
int BinarySearch(Const ElementType A[],ElementType X,int N)
{
int Low,Mid,High;
Low=0;High=N-1;
while(Low<=High)
{
Mid=(Low+High)/ 2;
if(X>A[Mid])
Low=Mid+1;
else
if(X<A[Mid])
High=Mid-1;
else
return Mid;//Found
}
return NotFound//is defined as -1;
}
每次循环使问题的规模减小一倍,故时间复杂度是O(logn);int GCD(int a , int b )//辗转相除法(Greatest Common Divisor)
{
int temp;
if(!(a%b))
{ return b;break;}
else
return GCD(b,a%b);//除数除余数
}
//都不用判断a,b大小,如果a<b,第一次递归或迭代会交换他们。
迭代写法(推荐):
int GCD(int M, int N) //(Euclid's algorithm)
{
int Rem;
while(N>0)
{
Rem=M%N;
M=N;
N=Rem;
}
return M;
}
if M>N,then M mod N < M/2;(If N<=M/2,then remainder is smaller than N;if N>M/2,then remainder is M-Nalso smaller than M/2);
考虑(a,b)$\rightarrow$(b,a mod b)这个迭代,有两种情况:
1,如果a>b,那么迭代两次后得到(a mod b,b mod (a mod b)),
有a mod b <
}
int gcd(int m,int n)更相减损术
{
if(m>n)
return gcd(m-n,n);
else if(n>m)
return gcd(m,n-m);//大数减小数
else
return m;
}设gcd(a,b)=c,lcm(a,b)=d,即ab的最大公因数为c,最小公倍数为d,则一定有a=k1*c , b=k2*c (1) a=d/t1 b=d/t2 (2),其中k1,k2必然互质(反证法:假设k1,k2不互质,则必定有一个大于1的最大公因数,设其为x,则有a=k1/x * xc, b=k2/x * xc,此时k1/x和k2/x已经互质,但是明显a和b有一个公因数xc,又因为x>1,则xc>c,和前提ab的最大公因数c矛盾,则k1,k2必然互质,同理可证t1,t2互质)
对于(1)式,可有b/a=k2/k1.对于(2)式,可有b/a=t1/t2,即k2/k1=t1/t2,定有常数y,使得k2=y*t1,k1=y*t2,即k2/k1=y*t1/y*t2=t1/t2,
而k2和k1是互质的,y只能为1,所以k2=t1,k1=t2,而k1=a/c,t2=d/b,所以a/c=d/b,即ab=cd,证毕
double f(double x)
{
return a3*(x)*(x)*(x)+a2*(x)*(x)+a1*(x)+a0;
}
double isroot(double a,double b)
{
if(fabs(f((a+b)/2))<1e-6)//也可用区间长度作为控制精度结束条件
return (a+b)/2;
if(f((a+b)/2)*f(a)<0)
return isroot(a,(a+b)/2);
else
return isroot((a+b)/2,b);
//Exponentiation:
long int Pow(long int x,int N)
{
if(N==0)
return 1;
if(N==1)//unneceaaary
return 1;
if(IsEven(N))
retuen Pow(x*x,N/2);
else
retuen Pow(x*x,N/2)*x;
}
O(log N)
void hanoi(int n, char A, char B, char C)//盘子数量,初始轴,中间轴,目标轴;
{
if (n == 1)//!最频繁的操作,是两个递归调用的终止条件
{
move(1,A, C);
return;//或else
}
hanoi(n - 1, A, C, B);//将A上面n-1个移动到B
move(n,A, C);//将A上最后一个最大的移动到C,也是移动每个子递归上最大的;
hanoi(n - 1, B, A, C);//将中间轴B上的移动到C
}
void move(int n,char A, char C)
{
cout << m++<<':'<<n<<"from" << A << " to" << C << endl;
}
Algorithm1:
int A[MAXN] = {0},i,j,temp;
for (i = 0; i < MAXN; )
{
srand(time(NULL));
temp = rand() % 10 + 1;
for (j = 0; j < i; j++)
{
if (temp == A[j])
break;
}
if(j==i)
A[i++]=temp;
}
The expected number of random numbers that need to be tried is N/(N-i), This is obtained as follows: i of the N numbers would be duplicates.Thus the probability of success is N-i/N(if成功的概率); Thus the expected number of independent trials is N/N-i(if 成功一次所需的次数);在x次独立重复事件中,该事件发生xp次;所以该事件发生一次的概率是1/p(两边同除以xp) The time bound is thus:
The time bound is thus
Algorithm2:
int A[MAXN] = {0},Used[MAXN]={0},i,j,temp;
for (i = 0; i < MAXN; )
{
srand(time(NULL));
temp=rand()%MAXN+1;
if(!Used[temp-1])
{
A[i++]=temp;Used[temp-1]=1;
}
}Obviously time complexity is O(nlogn);
Algorithm3:
for (i = 0; i < MAXN; i++)
{
A[i] = i + 1;
}
for (i = 0; i < MAXN; i++)
{
srand(time(NULL));
swap(A[i], A[rand() % (i+1)]);
}
The worst-case running time of algorithms I and II cannot be boundedbecause there is always a finite probability that the program will not terminate by some given time TO. The algorithm does, however, terminate with probability 1. The worst-case running time of the third algorithm is linear - its running time does not depend on the sequence of random numbers.
L = (a1, a2, a3,...,an). 表名 首元(head) 尾元(tail) ai:结点(数据元素) 没有元素时是空表。
要点:
1,表中元素具有逻辑上的顺序性;
2,表中元素个数有限;
3,表中元素都是数据元素(不可分);
4,元素的数据类型都相同(等价类型变量(union)也可以);
5,表中元素具有抽象性。
线性表的顺序存储.
动态存储结构就是在程序运行期间动态的分配内存。一维数组既可以动态存储也可以静态存储.
#define maxSize 30//静态存储
typedef int DataType;
typedef struct
{
DataType data[maxSize];
int n;
} Seqlist;#define maxSize 30//动态存储
typedef int DataType;
typedef struct
{
DataType *data;
int n;
} Seqlist;
void initList(Seqlist &L)
{
L.Data=(DataType*)malloc(sizeof(DataType));
if(!L.Data)malloc(sizeof(DataType));
exit(1);
L.Maxsize=InitSize;
L.n=0;
}最小是1,最多是n;
移动第ℹ-1到第n-1位置间共n-i+1个元素,最少移动0次,在第n+1个位置插入;最多移动n次,在第一个位置插入。
不要求顺序时可以直接插在后面。
把第i到第n-1共n-i个元素顺序前移,最少移动0个,最多移动n-1个。
不要求顺序时可以直接将最后一个元素覆盖要删除的元素。
各种操作的时间复杂度都是O(N),大小都是二分之最小加最大.
顺序表的缺陷:在插入和删除时需要频繁的执行成块的数据移动,所以主要用于不经常插入或删除的应用程序,它具有直接存取的特性。
也叫线性链表或单链表,是线性表的链接存储表示.
结构:为元素附加指针形成一个个结点(node),通过指针将各个数据元素按其逻辑顺序勾连起来,结点包括数据域(data)和指针域(链域)(link);第一个结点称为首元结点(表头指针指向),没有前置结点(predeceor).可以通过头指针(Header/Dummyhead)(有利于插入删除首元节点)找到,最后一个结点称为尾元结点(表尾指针指向),没有后继结点(successor);
一般用带头结点的,递归函数一般用不带头结点的,不带头结点更为简洁和通用.
链表非引用传入的指针只能改变它们之后的结点,如果不用返回值,而其本身结点的值(非成员值)需要改变,可以解引用赋值浅拷贝,也可以用成员运算符深拷贝,一般用前者即可。
typedef struct Node{
DataType data;
struct Node *Next;
Node(int val) :data(val),next(nullptr) {}
Node(Node *ptr):next(ptr){}
Node():data(0),next(nullptr) {}
Node(int val,node* ptr):data(val),next(nullptr){}
}LinkNode,*LinkList;
p=(LinkList)malloc(sizeof(LinkNode))=new LinkNode=new LinkNode()=new LinkNode(0)=new LinkNode(0,nullptr)=new Node(**);//可以用别名也可以用结构体名,类也一样
LinkList *cur = &Head, p;//注意取地址符和引用的区别
while (p = *cur)
{
if (p->data == x)
{
*cur = p->next;/*通过当前结点的指针(pred->next)的地址直接改变当前结点指针,直接赋值会使结点脱离(操作对象只是个中间变量P),所有需要维护或通过前置结点进行的操作例如插入,删除等都可以这样,也可以同时使操作不再依赖头结点(当然一般情况还是优先加头结点),频繁的插入删除优先采用此方法,注意指针起始地址,从首元结点开始:&head,从头结点开始:&header->next(!=&head(copy val))*/
free(p);
}
else
cur = &p->next;/*cur=&(*cur)->next;'->','.'优先级最高,'&','*'其次,取得链表结点指针的地址而不是中间指针变量的地址*/
}
{
LinkList *pcur = &Head;
cout << "Please enter " << num << "datas" << endl;
while (num--)
{
LinkList cur = new LinkNode;
if (!cur)
{
cout << "Memory allocation failed" << endl;
exit(1);
}
cin >> cur->data;
*pcur = cur;
pcur = &cur->next;
}
*pcur = nullptr;
}
/*注意辨析*pcur=(*pcur)->next(修改地址上的结点),pcur=&(*pcur)->next(移动结点,底层,借助指针地址)与cur=cur->next(移动结点,表面,借助中间变量)*/当慢指针从表头移动a次后快指针也将到达环的起点。
LinkNode *detectCycle(LinkNode *head) {
LinkNode *slow = head, *fast = head;
while (1)
{
if (fast && fast->next && (fast = fast->next->next))
{
slow = slow->next;
if (fast == slow)
break;
}
else
return nullptr;
}
slow=head;
while(1)
{
if(fast == slow)
return fast;
slow= slow->next;
fast= fast->next;
}
} ListNode *p = headA, *q = headB;
int gap = 0, flag = 0;
while (p || q)
{
if (!(p && q))
{
flag = p ? 1 : 0;//标记较长串
gap++;//长度差值
}
if (p)
p = p->next;
if (q)
q = q->next;
}
flag ? (p = headA, q = headB) : (p = headB, q = headA);
while (gap--)
p = p->next;
while (p != q)
{
p = p->next;
q = q->next;
}
return p;
fast=slow=head;
while (fast&& fast->next){//find mid node of linklist
slow = slow->next;
fast = fast->next->next;
}(1)存储利用率:
(2)空间限制:
顺序表只有在动态分配内存时可以扩充,但存储开销和时间开销大,效率低;单链表随用随申,一般没有存储溢出的问题,空间限制小;
(3)存储的占用方式:
顺序表的存储空间不随表的操作改变,事先估计不足或过大都会造成问题;链表占用空间随用随变,很灵活。
(1)存储结构特点:
顺序表用物理关系上的邻接关系来表示结点间的逻辑关系,结构简单;链表元素的物理存储位置和逻辑链接关系不一定一致;链表结点间的存储一般是不连续的,但链表结点内部的存储空间是连续的。
(2)访问方式:
顺序表可以从前往后或从后往前或按下标存取,链表只能沿着指针逐个节点存取,顺序表查找比链表快;
(3)插入删除速度:
顺序表平均要移动一半元素,链表只需要修改链接指针,无需移动元素;
如果表头指针被保护,单链表的安全保密性比顺序表好.
顺序表适合频繁查找,不适合频繁插入删除,链表反之。
其他链表的逻辑结构也是线性表.
栈,队列和双端队列的逻辑结构与线性表相同,但有更多限制(restrictions),称为运算受限的线性表或限制了存取点的线性表.
class SeqStack
{
public:
DataType *elem;
int maxSize, top;
SeqStack(int size) : maxSize(size), top(-1), elem(new DataType[size]) {}
SeqStack(const vector<DataType> &value) //利用vector初始化
{
maxSize = value.size();
top = maxSize - 1;
elem = new DataType[maxSize];
for (int i = 0; i < maxSize; i++)
elem[i] = value[i];
}
~SeqStack() { delete[] elem; }//释放内存
} ;可定义为只允许在表的末端进行插入和删除操作的线性表(LIFO,Last In First Out),允许操作的一端叫栈顶(top),另一端叫栈底(bottom),没有元素时叫空栈,主要操作是Pop(出栈)和Push(进栈).
栈空时退栈要进行栈空处理,栈满时入栈要进行栈满处理,它们不是出错处理,而是使用这个栈的算法结束时需要执行的处理(It's an implementation error but not an ADT error)
栈的基本性质:(1):集合性;(2):线性;(3):运算受限;(4):数学性质;
栈在生命周期内的状态:栈满,栈空,栈半满;可能的操作:进栈(入栈),出栈(退栈),置空;
合理的S/X序列满足:(1):最终S==X;(2):任意状态S>=X;
顺序栈的优点是存取速度快,插入,删除方便;缺点是容量不好把握,空间利用率底,多栈共享空间时效率低。
链栈的优点是插删方便,不存在栈满的问题,同时使用多栈时效率高,便于共享空间。缺点是需要额外空间存放指针域。
单调栈不一定是栈内的元素本身单调,也可能是储存的数组下标对应的元素单调,这样存储的信息更多。注意数组最后哨兵的添加。
通过控制入栈和退栈时机得到不同的退栈序列.
不可能的退栈序列:例如进栈时按$\cdots p_i\cdots p_j\cdots p_k\cdots$次序,则$\cdots p_k\cdots p_i\cdots p_j\cdots$就是不可能的出栈序列,因为当$p_k$出栈时,$p_i$和$p_j$在其之前入栈,故还按原顺序在栈内,$p_i$先进于$p_j$,不可能先出于它。即在某个出栈元素之前进栈且之后出栈的几个元素,出栈后在该元素之后的顺序遵循先进后出。
判断是否为可能的退栈序列更直观的分析方式是根据最后一个出栈的元素将原序列分段,比它(序号)小的元素(如果存在)比他先入栈也先出栈,比它大的元素(如果存在)随后出栈,且这两部分本身也满足这个规律,具体就是将原序列递归拆解为许多n<=3的序列,拆解时大区域和小区域混合或拆解成的序列存在不可能退栈序列则该序列为不可能退栈序列。n=0,1,2,3,时只有n=3时的312是不可能序列,例如dbca,没有小区域,只有大区域,但大区域是312型,故为不可能序列,dabc,大小区域混合。
卡特兰数(catalan)推导:对于任意的出栈序列,设最后一个元素序号是k,则比最后一个元素小的有k-1个,比它大的有n-k个,根据前面说明这两部分也是可能出栈序列并相互独立,满足乘法原则,设可能出栈序列数为f(k),则f(k)=f(k-1)*f(n-k),k属于1到n,不同k的情况满足加法原则,故总的可能序列数是f(n) = f(0)f(n-1) + f(1)f(n-2) + …… + f(n-1)f(0)。$C_{n+1}=\sum_{i=0}^n C_i\times C_{n-i} = \frac{1}{n+1}C_{2n}^n = \frac{1}{n+1}\times \frac{(2n)!}{n!\times n!}=\frac{2n(2n-1)\cdots(n+2)}{n!}$详细证明
(1)全部压栈再边退边和原序列比较;(2):压栈一半再边退栈边和剩余的一半比较;中点容易确认或已确认的用2;
将待排元素放在辅助栈,将目标栈栈顶元素与辅助栈新出栈元素比较,满足大小关系或空栈则入目标栈,否则目标栈退栈到到辅助栈直到满足关系或空栈,辅助栈空时退出。
十进制与k进制数的关系:$N=\sum_{i=0}^{[\log_k^N]}(b_i\times k^i),b_i=0,1,\cdots,k-1$
例如,$49_{10}=1\times 2^5+1\times 2^4+\cdots +1\times 2^0=110001_2$
这样,十进制数N可以用长度为$[\log_k^N]+1$位的k进制数表示为$b_{[\log_k^N]}\cdots b_2b_1b_0$
不断通过取余取商可以将$b_0到b_{[\log_k^N]}$顺序求出来,先全部入栈最后出栈就可以顺序输出。
遇到左括号进栈,遇到右括号出栈(多种括号需比较后出栈),如果中途出栈时栈空(一种括号)或没有与右括号匹配的左括号(多种)或者最终栈不空则匹配失败。
使用计数器只能处理一种括号的情况,([)]的情况将误判。
注:用vector<string>代替string可实现更大范围的输入;
算数表达式分为:前缀,中缀和后缀表达式;一般输入的表达式是中缀表达式,后缀表达式也叫RPN即逆波兰表达式,不用考虑优先级,程序计算时使用,它们的区别在于运算符的位置,运算数的相对位置是一样的。
运算符之间的优先级可以用算符优先矩阵或数字表示;
| 操作符op | $ | ( | ! | ^ | *,/,% | +,- | ) |
|---|---|---|---|---|---|---|---|
| isp(栈内) | 0 | 1 | 9 | 7 | 5 | 3 | 10 |
| icp(栈外) | 0 | 10 | 8 | 6 | 4 | 2 | 1(无实际意义) |
-
左括号在栈外的优先级最高,使它前面的表达式先搁置,进栈后优先级极低,使得后面的表达式进入,遇到进入的右括号优先级极低,使后面的表达式先搁置,直至括号相遇一起出栈,满足括号内优先级最高。
-
表达式进入栈内后优先级增加,满足同级从左到右的优先级。
-
开头结尾的标志相遇后栈空结束,标志一般用\0,处理前在栈内加入\0,与字符串结尾的\0配对。前者与第一个读取元素比较,后者用于结束,(便于方便应使用char *字符串输入,string无结尾0,可将string.c_str()拷贝到char *P上,注意预先给P分配s.length()+1个空间,然后修改原串,免于返回(注意要引用string))
具体算法:
(1),初始化栈,将结束符\0进栈,开始读入表达式串;
(2),重复执行以下步骤直到遇到ch=='\0',与最后的栈顶配对并退栈然后停止循环。
-
如果ch是操作数直接赋给结果串;
-
如果ch是操作符,比较ch与栈顶元素的优先级;
-
if icp(ch)>isp(op),进栈,读下一个字符;
-
if icp(ch)<isp(op),退栈赋给结果串;
-
if icp(ch)==isp(op),退栈,如果没到结尾就读入下一个字符;
-
顺序扫描表达式,操作数进栈,遇到二元操作符,连续退出两个操作数Y和X,形成运算指令X<op>y,一元操作符退出一个,形成指令X<op>,并将结果重新入栈,表达式扫描完后,栈顶存放的就是计算结果。
/*也可以将EnQuene作为类的友元,这时它的声明可以放在后面*/
/*class CircQueue; //前向声明,作为EnQuene的形参
bool EnQueue(CircQueue &Q, DataType x); //结构体调用,需在其之前声明;*/
class CircQueue
{
public:
DataType *elem;
int maxSize;
int front, back;
friend bool EnQueue(CircQueue &Q, DataType x);//类和非成员函数友元不需要提前声明
CircQueue(int size) : maxSize(size + 1), front(0), back(0), elem(new DataType[size + 1]) {}
/*注意预留一个位置*/
CircQueue(vector<DataType> &value)
{
maxSize = value.size() + 1; //不能调用另一个构造函数,因为这一个还没构造完
elem = new DataType[maxSize];
front = back = 0;
for (int i = 0; i < value.size(); i++)
EnQueue(*this, value[i]); //全局函数(已声明或友元)可直接调用,与成员函数同名时前加::
}
~CircQueue()
{
delete[] elem;
}
};只允许在队头(front)插入,队尾(back)删除,先进先出(FIFO);
初始时,rear=back=0,当back==maxSize时队满,但rear可能不是0,形成假溢出,为了充分使用数组的空间,把数组的前端和后端连接起来,形成一个环形的表,即把存储元素的表逻辑上看做一个环,成为循环队列。
队列的头尾指针时同向运动,栈是反向运动;
队头/队尾指针进一:ptr=(ptr+1)%maxSize;
为了使队满条件区别于队空条件,用(back+1)%maxSize==front来判断是否队空,队满时空了一个位置,不空就无法区别,所以设置初始容量时要预留一个位置。
其它实现方式:
(1)元素进队时tag设为1,用back==front&&tag==1判断队满,元素出队时tag设为0,用back==front&&tag==0判断队空;
(2)记录队列长度;
双端队列(double-ended queue),允许在两端插入和删除,输出受限时有三种可能的输出:(1):在同一端输入输出,相当于栈;(2):在一端输入,另一端输出,相当于队列;(3):混合进出;优先队列:取出的不是最先加入的而是优先级最高的(输出时需要遍历数据)。
逐行输出杨辉三角形;
void PrintTriangle(int n)
{
LinkQueue Q;
EnQueue(Q, 1);
EnQueue(Q, 1);
for (int i = 1, t = 0; i <= n; i++)
{
EnQueue(Q, 0); //每一行之间添加0,便于计算最右侧的数
for (int j = 1; j <= i + 2; j++)
{
EnQueue(Q, GetFront(Q) + t); //计算下一行并入列
t = DeQueue(Q); //保留以计算下一个下一行的元素
if (j == 1)//保留行前空格
cout << setw(n - i + 2) << setiosflags(ios::right)<< setfill(' ') <<t<<' ';
else if (j != i + 2) //输出本行,除了添加的0
cout << setw(2) <<setiosflags(ios::left)<< t << ' ';
}
cout << endl;
}
}对于数组$a[m_1][m_2]\cdots[m_n]$,
上下三角矩阵非零元素个数是:$\frac{n(n+1)}{2}$,三对角矩阵非零元素个数是$3n-2$
行优先存储下三角钜阵的访问地址:$\frac{i(i+1)}{2}+j,i,j\geq 0$
行优先存储上三角矩阵的访问地址:$\frac{i(2n-i-1)}{2}+j$
行优先存储三对角矩阵的访问地址:$2\times i+j$
互换i,j就是列优先。
反解可由压缩数组映射到矩阵;
稀疏因子$\delta=\frac{t}{m\times n}$;通常当这个值小于0.05时可以认为是稀疏矩阵。对于nxn的当非零元素数小于$\frac{n^2}/{3}$时是稀疏矩阵,某些场合应小于$\frac{n^2}/{5}$
三角矩阵是稠密矩阵,三对角矩阵当n>8时是稀疏矩阵
以下存储方法都失去了直接存取的特性,只能顺序查找;
class Triple
{
int row,column;
Datatype value;
};
class SpareMatrix
{
int rows,cols,terms;
Triple elem[MAXN];
}
//还可以改进,例如添加标识每行首个非零元素位置的数组,这样还可以只使用二元组,不用额外储存行号(数组进一位就标志到新行),具体实现最方便的就是在输入的时候放在每一行的terms(当前总数)位置上(上一行的下一个位置),也可以根据已建立的三元组表计算
//计算每行非零元素开始位置
int rowSize[a.rows],rowStart[a.rows];
for(int i=0; i<a.terms; i++)//计算每一行非零元素的数量
rowSize[a.elem[row]]++;
rowStart[0]=0;
for(int i=1;i<a.terms;i++)
rowStart[i]=rowStart[i-1]+rowSize[i-1];//递推式;(1)简单链表存储;
(2)行链表组;
(3)正交链表(十字链表);
头结点和非零元素结点的共有部分是tag,down,right;不同的部分是头结点有next,非零元素结点有col,row和val;总的头结点结构像两种结点的叠加,和元素结点一样的特有部分变成了rows,cols,和size;已知行列数时头结点用数组存储比较方便;
P 的 next 数组定义为:next[i] 表示 P[0] ~ P[i-1] 这一个子串,使得 前k个字符恰等于后k个字符 的最大的k. 特别地,k不能取i+1(因为这个子串一共才 i+1 个字符,自己肯定与自己相等,就没有意义了)。
性质:P[0] 到 P[i] 这一段子串中,前next[i]个字符与后next[i]个字符一模一样。既然如此,如果失配在 P[r], 那么P[0]~P[r-1]这一段里面,前next[r]个字符恰好和后next[r]个字符相等——也就是说,我们可以拿长度为 next[r] 的那一段前缀,来顶替当前后缀的位置,让匹配继续下去.
另一种思考:如果某一次匹配后失配字符前配合部分的最长前缀p0...pn-2不等于最长后缀p1...pn-1;则如果从主串的下一个字符开始匹配必定失配,因为这次匹配的开头部分相当于刚才假设的不相等串匹配(相等传递),(而BF算法不考虑这个,每次失配只进行这一步),继续考虑次长前后缀P0...pn-3,p2...pn-1,此时模式串移动的距离相当于第一次失配后按BF算法的第二次匹配,直到第k次考虑找到最大相同前后缀前面这一段才可能匹配成功,这时模式串后移距离相当于BF算法第一次失配后的第k次匹配,所以可以直接进行BF第k次,并直接从失配字符而非从头继续匹配(移过去之后前面这一段是公共部分,具体距离最大相同前后缀的长度+1),主串不用动,通过j=next[j]就将模式串调到合适的地方,j向前移实现模式串向后走。
主串影响失配的位置和多少,模式串影响回溯的步数;
next失配函数定义: $$next(j)=\begin{cases}-1;j=0\ k+1;0\leq k<j-1且使得p_0p_1\cdots p_k=p_{j-k-1}p_{j-k}\cdots p_{j-1}的最大整数\ 0,其它情况\ \end{cases}$$
求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。最大步增为1,最小值为0;
void getNext(char * p, int * next)
{
next[0] = -1;
int i = 0, j = -1;
while (i < strlen(p))
{
if (j == -1 || p[i] == p[j])
{
j++;
next[++i] = j;//下一位的next值是包括当前位最长前后缀的长度加1;
}
else
j = next[j];
}
}
int KMP(char * t, char * p)
{
int i = 0;
int j = 0;
while (i < strlen(t) && j < (int)strlen(p))//-1与size_t比较会转为uint,需要转换
{
if (j == -1 || t[i] == p[j]) //当p[0](后面最差情况会转到0)与失配的t[i]匹配不上时j会等于-1,即模式串与t[i+1]对齐,next数组的作用就是利用已经配对过的部分控制模式串的偏移量
{
i++;
j++;
}
else
j = next[j];
}
if (j == strlen(p))
return i - j;模式串的位置
else
return -1;
}
广义表,又称列表,也是一种线性存储结构。同数组类似,广义表中既可以存储不可再分的元素,也可以存储广义表,记作:
LS = (a1,a2,…,an)
其中,LS 代表广义表的名称,an 表示广义表存储的数据。广义表中每个 ai 既可以代表单个元素,也可以代表另一个广义表。
通常,广义表中存储的单个元素称为 "原子",而存储的广义表称为 "子表"。
例如创建一个广义表 LS = {1,{1,2,3}},我们可以这样解释此广义表的构成:广义表 LS 存储了一个原子 1 和子表 {1,2,3}。
以下是广义表存储数据的一些常用形式: A = ():A 表示一个广义表,只不过表是空的。 B = (e):广义表 B 中只有一个原子 e。 C = (a,(b,c,d)) :广义表 C 中有两个元素,原子 a 和子表 (b,c,d)。 D = (A,B,C):广义表 D 中存有 3 个子表,分别是A、B和C。这种表示方式等同于 D = ((),(e),(b,c,d)) 。 E = (a,E):广义表 E 中有两个元素,原子 a 和它本身。这是一个递归广义表,等同于:E = (a,(a,(a,…)))。
注意,A = () 和 A = (()) 是不一样的。前者是空表,而后者是包含一个子表的广义表,只不过这个子表是空表。
当广义表不是空表时,称第一个数据(原子或子表)为"表头",剩下的数据构成的新广义表为"表尾"。
强调一下,除非广义表为空表,否则广义表一定具有表头和表尾,且广义表的表尾一定是一个广义表。
例如在广义表中 LS={1,{1,2,3},5} 中,表头为原子 1,表尾为子表 {1,2,3} 和原子 5 构成的广义表,即 {{1,2,3},5}。
再比如,在广义表 LS = {1} 中,表头为原子 1 ,但由于广义表中无表尾元素,因此该表的表尾是一个空表,用 {} 表示。
由于广义表中可以同时存储原子和子表两种类型的数据,因此在计算广义表的长度时规定,广义表中存储的每个原子算作一个数据,同样每个子表也只算作是一个数据。
例如,在广义表 {a,{b,c,d}} 中,它包含一个原子和一个子表,因此该广义表的长度为 2。
再比如,广义表 {{a,b,c}} 中只有一个子表 {a,b,c},因此它的长度为 1。
前面我们用 LS={a1,a2,...,an} 来表示一个广义表,其中每个 ai 都可用来表示一个原子或子表,其实它还可以表示广义表 LS 的长度为 n。 广义表规定,空表 {} 的长度为 0。
广义表的性质:
(1):有次序性:各表元素在表中线性排列;
(2):有长度:各表元素个数一定,不能是无限的;
(3):有深度:表中括号的重数即为深度,递归表的深度是无穷大;
(4):可递归:具有这种性质的表为递归表;
(5):可共享:广义表可被其它表共享,被共享的表叫共享表或再入表;
由广义表的性质可知,广义表有深度,它是一种层次结构;广义表有共享性,它是一种有向图;广义表的表元素有次序,它类似于一种线性结构,但只有所有表元素都为原子时才退化为线性表,广义表是一种非线性结构。
第一种将原子看作只有一个元素的子表,通过子表互相连接;第二种将两者区分开都是同深度的互相链接;
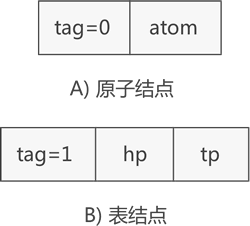
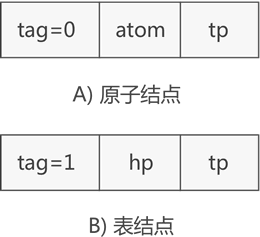
前两种插删都比较困难,为拓展线性链表表示的每个字表添加一个头结点可简化插删,这种表示有三种结点:原子结点,字表结点,头结点;
字表结点hlink从指向字表首元结点变为指向字表头结点;
用3种tag区分;
表示n元多项式的结点定义:
class PolyNode
{
PolyNode* tlink;//同一层下一结点指针
int exp;//指数
int tag;//标志,=0为头结点,=1为子表结点,=2为原子结点;
union
{
char name;//表头链表中存放的基于该链表的变量名
PolyNode *hlink;//指向系数子链表的指针
double coef;//系数
}
}
子表结点中exp是本条链表的变量(头结点name变量)的指数;
将每个子表结点下不同层的多项式相乘的结果相加即为本条链表储存的结果。
一棵树是n(n>=0)个结点的有限集合,n=0时为空树,而非空树可记作$T={r,T_1,T_2,\cdots,T_n}$,其中,r是T的根结点,$T_1,T_2,\cdots,T_m$是除r外其它结点构成的互不相交的m个子集合,子集合也是一棵树,称为根的子树。
每棵子树的根节点有且仅有一个直接前驱(即它的上层结点),但可以有0个或n个直接后继(即它的下层结点),m称为r的分支数。
树的定义是一个递归的定义,即树的定义中又用到了树的概念。
除了逻辑表示外,树还有目录结构表示,韦恩图表示,凹入式表示和广义表表示;
结点,结点的度(子树棵数),叶结点(度为0的结点),分支结点(度不为0),子女结点,双亲结点,兄弟结点,祖先结点(由根结点到该结点路径上的所有结点(一般指真祖先),子孙(后裔)结点(一般指真子孙),结点间的路径,结点的深度(结点所属层次,以最上为基准),结点的高度(叶结点的高度为1,有的教材定义为0,非叶节点的高度等于它子女结点高度中的最大值加一,以最下为基准),树的深度(距离根结点最远的结点所处层次),数的高度(等于根结点的高度,值与树的深度相等),树的宽度(每一层结点个数的最大值),树的度(树中结点的度的最大值,度为n就是n叉数),有序树(各棵子树次序是定的),无序树(子树次序不定),森林(是m,m>=0棵树的集合,删去一棵树的根结点,树就变成森林(森林可能为空),反之,将几棵树连接到一个根结点,树就变成森林);
一些结论:
-
树中的分支条数等于结点条数减一;
-
树中任意两个结点之间有且仅有一条路径;
-
树中每对结点至少存在一个共同祖先;
-
一对结点的有且仅有的深度最大的祖先结点称为最低共同祖先;
-
所有结点的度数之和为n-1(计算度的时候除了根结点都被计算了一遍);设度为$k_i$的结点有$m_i$个,则$\sum_{i}^{n}m_i-1=\sum_{i}^{n}(m_i\times k_i)$
-
高度为k的满n叉树的最大宽度为$n^{k-1}$结点总数为:$\sum_{i=1}^{k}n^{i-1}=\frac{n^{k}-1}{n-1}$,反解可得结点总数为n的m叉树的最小深度为$\lceil\log_m(n(m-1)+1\rceil$,(列式时n大于上层最大总数,小于等于本层最大总数)
-
从1开始自顶向下给一个N叉树的结点编号,则编号为i的结点的双亲结点编号为$\lfloor i/N\rfloor$;
$T=\begin{cases}\emptyset,n=0 \ {r,T_L,T_R}\ \end{cases}$
特殊二叉树
-
完全二叉树:上面从第一层到第k-1层的结点数都是满的,仅最下面的第k层或是满的,或是集中存放在左侧,最多有$2^k-1$个结点,最少有$2^{k-1}$个结点;
-
满二叉树:满的完全二叉树,第k层有$2^{k-1}$个结点;
-
理想平衡树(丰满树):上面是满的,最后一层的结点散见于该层各处;
-
最多有两个子树,分别称为左子树和右子树,子树可以为空但不能说没有;
-
二叉树的定义是递归的;
-
二叉树可能有5种不同的形态,n叉树可能有$\sum_{i=0}^{n}C_n^i+1(空树)$;
-
关于树的术语二叉树都适用,但二叉树不是树(图论)(定义没有唯一的标准);
-
树在图论中被视为用n-1条边联结n个顶点的特殊的图,图的顶点集合非空,故树的顶点集合非空。图论中另外定义了N叉树,它可以是空树,二叉树属于N叉树;
-
非空二叉树有根,根结点的子树有左右之分,树可以没有根(自由树),子树也没有顺序区分;
-
-
第i层(i>0)最多有$2^{i-1}$个结点;
-
深度为k(k>=0)的二叉树最少有k个结点,最多有$2^k-1$个结点;
-
对于任意一棵非空二叉树,若其叶结点数为n0,度为2的结点数为n2,则$n_0=n_2+1,(n_0+n_1+n_2-1=n_1+2n_2)$,两者一奇一偶,和为奇数。
-
具有n个结点的完全二叉树或理想平衡树的深度为$\lceil\log_2(n+1)\rceil$或$\lfloor log_2n \rfloor+1$,区别来源于列式时是$2^{d-1}-1<n\leq2^d-1$还是$2^{d-1}\leq n<2^d$,后者不适用等于0的情况。
-
将完全二叉树自顶向下,同一层从左往右从1开始编号,则有以下关系:
-
奇数结点在右兄弟位置(除根结点),偶数在左兄弟位置
-
结点i的双亲为结点$\lfloor i/2 \rfloor ,i>1$;
-
结点i的左子女为2i,2i<=n,右子女为2i+1,2i+1<=n;
-
结点i所在的层次为$\lfloor\log_2i\rfloor+1$;
-
编号最大的非叶结点为$\lfloor \frac{n-1}{2}\rfloor+1$
-
从0开始编号时双亲结点公式用i-1替换,其余用i+1替换,左右对应关系对调;
-
-
完全二叉树度为1的结点只有0个或1个,当n为奇数时,因为n0+n2是奇数,所以n1=0,此时称为严格(正则)二叉树(结点最少为2h-1,最多为2^h-1),n为偶数时n1=1;$n_0=n/2,n_2= n/2-1 $,完全二叉树的叶结点数量大于等于非叶结点数量。
-
有n个结点,高度为n的二叉树的棵数为$2^{n-1}$,每个向下的子女都有两个可能的位置。
-
满二叉树某一行的结点数$2^{h-1}=\lceil \frac{n}{2} \rceil,n是该行及其以上结点的总数2^{h}-1$
顺序存储,将元素顺序排列在数组里,可用'#'表示空结点,只适合存储完全二叉树,存储空结点多的二叉树浪费空间,数组大小是$2^h-1$
链表存储
二叉链表链指针个数是2n,n+1个是空的,n-1个指向子女,等于边数。
class TreeNode
{
public:
DataType data;
TreeNode *lchild, *rchild;
TreeNode() : data(0), lchild(nullptr), rchild(nullptr) {}
TreeNode(DataType val) : data(val), lchild(nullptr), rchild(nullptr) {}
TreeNode(DataType val,TreeNode *rptr,TreeNode *lptr): data(val), lchild(lptr), rchild(rptr){}
};
typedef TreeNode *BinTree;
//加一个指向双亲的指针即为三叉链表表示所谓二叉树遍历(binarytree traversal)遵从某种次序,便访二叉树中的所有结点,使得每个结点被访问一次且只访问一次。
共有6种规则:VLR,LVR,LRV,VRL,RVL,RLV,规定先左后右后剩下3种规则,VLR(先序遍历),LVR(中序遍历),LRV(后序遍历),递归实现语句区别在于访问语句和递归遍历语句的相对顺序;
(1+2*3)+2*3*4的先序,中序,后序遍历结果(前,中,后缀表达式)
+ * 4 * 3 2 + * 3 2 1
4 * 3 * 2 + 3 * 2 + 1
4 3 2 * * 3 2 * 1 + + 特别的,中序遍历序列就是二叉树在底面的投影。
非递归实现语句较复杂但时间和空间复杂度会降低(不降低数量级),大体都是先从根结点开始沿着左分支下行,并在栈中记录当前结点位置,最后把控制权交给栈顶右子女将其作为新的根结点,区别在于访问结点语句的位置和转交控制权语句的位置,特别的,后序非递归实现时栈内保存的是某一结点和它任意祖先之间的路径。
设有n个结点,遍历算法的时间复杂度为O(n)(每个结点只访问一次),空间复杂度最好为$O(log_2n)$,最差为O(n),递归工作栈最多存放的结点数等于树的高度(单支树等于n),对于递归算法,每次递归就向下一层,也等于树的高度。
层次序遍历(广度优先)的时间复杂度为O(n),空间复杂度最大为树的宽度O(n/2)=O(n),队列最多存放$\lceil \frac{n}{2} \rceil$个结点
| 先序 | 中序 | 后序 | |
|---|---|---|---|
| 左单支树 | 正向 | 逆向 | 逆向 |
| 右单支树 | 正向 | 正向 | 逆向 |
输出序列从上向下为正向。
若先序遍历时u在v之前且后序遍历时在u在v之后,则u是v的祖先。
二叉树的重构:通过二叉树的遍历序列忠实(唯一)地还原出二叉树的拓扑结构.
-
(先序||后序)+中序;可以通过数学归纳法证明,重构算法是遍历前序(从前向后)或后序序列(从后往前),并在中序序列中将遍历到的结点作为根结点将两个序列拆分开(根,左,右),不断递归进行,中序决定左右子树序列的长度,先序+后序不行是因为归纳证明时若一个子女为空则通过(t,L/R)和(R/L,t)不能确定该子女是左还是右。
-
1,找到当前层序序列中 第一个 出现在当前中序序列的元素 作为根节点root,2,在当前中序序列中找出根节点root的下标k,把当前中序序列划分为[inL,k-1],[k+1,inR],分别是 当前根节点root的 左子树的中序序列,和右子树的中序序列。
-
由完全二叉树的任意一种遍历序列都可以实现二叉树的重构。
-
根据前序和后序可以重构一棵真(严格)二叉树,因为它不会出现根结点一个子女为空的情况,重构算法是用分治策略,具体是找到根结点和左右子女分界位置并递归地对左右子女进行重构。前序序列:(t,L(...),(R...)),后序序列:((...L),(...R),t)根结点就是前序序列的第一个结点和后序序列的最后一个结点,后序序列的分界点就是前序序列根结点的左子女在后序序列中的位置,对称的可以找到前序序列的分界点。
TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder) {
return create(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
}
TreeNode* create(vector<int>& preorder, vector<int>& inorder, int ps, int pe, int is, int ie){
if(ps > pe){
return nullptr;//子树为空
}
TreeNode* node = new TreeNode(preorder[ps]);//对于后序是pe
int pos;
for(int i = is; i <= ie; i++){
if(inorder[i] == node->val){//在inorder里寻找子根作为分界点
pos = i;
break;
}
}
node->left = create(preorder, inorder, ps + 1, ps + pos - is, is, pos - 1);//左子树序列长度为pos-is
node->right = create(preorder, inorder, pe - ie + pos + 1, pe, pos + 1, ie);//右子树序列长度为ie-pos
/*利用中后序构造: node->left = create(inorder, postorder, is, pos - 1, ps, ps + pos - is - 1);
node->right = create(inorder, postorder, pos + 1, ie, pe - ie + pos, pe - 1); */
return node;
}
BinTree CreateByInAndLevel(string in, string level, int ie, int is, int ls)
{
if (is > ie)
return nullptr;
int index = -1;
while (index == -1)//找出层次序列中第一个出现在当前中序序列的元素(越过另一子树的元素)
{
for (size_t i = is; i <= ie; i++)
{
if (in[i] == level[ls])
{
index = i;
break;
}
}
ls++;
}
ls--; //多加了一个
BinTree root = new TreeNode(level[ls]);
root->lchild = CreateByInAndLevel(in, level, index - 1,is, ++ls);
root->rchild = CreateByInAndLevel(in, level, ie, index+1, ++ls);
return root;
}二叉树的计数:假设一个二叉树有n个结点,并对各个结点编号,先序遍历得到的叫先序排列,中序得到的叫中序排列,设先序排列是1到n,则中序排列数决定能确定多少棵二叉树。
递推公式为$\begin{cases}b_0=1,n=0\b_n=\sum_{i=0}^{n-1}(b_i\times b_{n-i-1}),i\geq1\\end{cases}$
结果为卡特兰数$\frac{1}{n+1}C_{2n}^n =\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!}= \frac{2n(2n-1)\cdots(n+2)}{n!}$
int numTrees(int n) {
vector<int> t(n + 1, 0);
t[0] = t[1] = 1;
int i, j;
for (i = 2; i <= n; ++i)
{
for (j = 1; j <= i / 2; ++j)//结构是对称的,计算一半再乘二较为简便(奇数项的中间项只有一项,后面再加)
t[i] += t[j - 1] * t[i - j];
t[i] *= 2;
if (i % 2)//加上奇数项的中间项
t[i] += t[i / 2] * t[i / 2];//Plus the middle 'root' trees.(结点子女相同)
}
return t[n];
}public:
vector<TreeNode *> generateTrees(int n)
{
if (n == 0)
return {} ;//return vector<TreeNode *>(0),a NULL vector;
return helper(1, n);
}
private:
vector<TreeNode *> helper(int start, int end)
{
vector<TreeNode *> res;
if (start > end)
{
res.push_back(NULL);
return res;
}
for (int i = start; i <= end; i++)
{
vector<TreeNode *> left = helper(start, i - 1);//分治
vector<TreeNode *> right = helper(i + 1, end);
for (int j = 0; j < left.size(); j++)//遍历所有组合
for (int k = 0; k < right.size(); k++)
{
TreeNode *root = new TreeNode(i);
root->left = left[j];
root->right = right[k];
res.push_back(root);
}
}
return res;
}线索二叉树
对一棵二叉树中所有节点的空指针域按照某种遍历方式加线索的过程叫作线索化,被线索化了的二叉树称为线索二叉树。
struct TBNode
{
char data;
int ltag,rtag;
struct TBNode *lchild;
struct TBNode *rchild;
};对于中序遍历的二叉树,左子女为空时会丢失前置结点,右子女为空时会丢失后置结点,为这两种情况找到对应的结点就建立了中序线索二叉树。
void InThreaded(TBNode *p,TBNode *&pre)
{
if(p){
InhTreaded(p->lchild,pre);//递归线索化左子树
if(p->lchild==nullptr){//当前结点左子女为空则设置前置结点
p->lchild=pre;
p->ltag=1;
}
if(pre&&p->rchild=nullptr)//将当前结点设置为非空的空右子女前置结点的后置结点
{
pre->rchild=p;
p->rtag=1;
}
pre=p;//当前结点是右子树的前置结点
InTheaded(p->rchild,pre);
}
}
int main(){
Create(T);
TBNode *pre=nullptr;
if(T)
{
InTheaded(T,pre);
pre->rchild=nullptr;
pre->rtag=1;//设置最后一个结点的后置结点为空
}
}先序和后序线索化类似。
子女—兄弟表示
寻找子女的复杂度是O(d),寻找双亲的复杂度是O(n);
左指第一个孩子,右指兄弟
树转化为二叉树,将树的根结点变为二叉树的根结点,再将树的左子女转化为二叉树并链接在二叉树的左子树上,最后将左子女的兄弟结点转换为二叉树并迭代链接在二叉树子女的右支上。转换得到的二叉树根没有右子女。
相当于将树右旋45度,向右平行的兄弟连支变为了向右下的右连支,向下的子女连支变为了向左下的左连支。
类似可得二叉树到树的转化。
去掉根结点的子女不唯一的树就是森林
树的遍历
先根遍历和中根遍历为深度优先遍历,层次序遍历为广度优先遍历。
树的路径长度是根结点到每一个结点的路径长度(结点的深度减一)之和
n个二叉树的最小路径长度$PL=\sum_{i=0}^{n-1} \lfloor\log_2{i+1}\rfloor=(n+1);\lfloor\log_2n\rfloor-2^{\lfloor\log_2{n+1}\rfloor}+2$,此时二叉树为完全二叉树。
对于一颗已有的二叉树, 如果我们为它添加一系列新结点,使得它原有的所有结点的度都为2,那么我们就得到了一颗扩充二叉树
外结点数(叶) = 内结点数 + 1 总结点数 = 2 × 外结点数 -1 (n+n-1)
将权值{w1,w2,...,wn}(wi>=0)分别赋给T的n个叶节点,称T为权值为{w1,w2,...,wn}的扩充二叉树,带有权值的叶节点叫做扩充二叉树的外结点,其余结点叫做内结点。
扩充二叉树的带权路径长度定义为$WPL=\sum_{i=1}^nw_il_i$,WPL最小时即为Huffman树。
带权路径长度最小的扩充二叉树不一定是完全二叉树,权值越大的离根结点越近的是。
Huffman算法(构造huffman树)
构造n个带有权值的结点组成的森林,将权值较小的两棵树合并,合并后的新根的权值为其子女结点权值之和,合并到只剩一棵树,所得的树就是huffman树。
限制外结点大小顺序可得唯一确定的树
//静态三叉链实现
using DataType = char;
struct HFNode
{
DataType data;
int weight;
int parent, lchild, rchild;
HFNode(int w = -1, DataType val = 0, int par = -1, int lc = -1, int rc = -1) : weight(w), data(val), parent(par), lchild(lc), rchild(rc)
{
}
};
struct HFTree
{
HFNode *elem;
int leafNum, totalNum, root;
~HFTree() { delete elem; }
};数组中前n个是外结点,后n-1个是内结点,第2n-2个是根结点,构造的时间复杂度为o(n^2);
最优判定树
用Huffman树建立的成绩查询树的WPL不一定是最优判定树,因为有的内结点判定等同于两次判定,权值会比预期的大。
改进算法与Huffman算法的区别是轮流检查权值和最小的相邻两树并进行合并,并且排列时相对顺序不能变化(可以在数组中将合并后的根结点与原左子女的位置交换,将右子女移到交换后左子女的前一个位置,中间部分顺序前移,最终根结点在第一个元素处),用链式表实现较为容易(静态表子女的位置改变后不能追踪)。
Huffman编码
将二叉树的左分支标记为0,右分支标记为1,从根结点到叶节点的路径唯一的表示了该叶节点的二进制编码。
设计变长编码,为出现概率较低的字符指定较长的码字,为出现概率较大的字符指定较短的码字,可以明显提高传输的平均性能。
前缀性质:任一字符编码都不是其它字符编码的前缀。用二叉树表示可以保证这个性质。
平均编码长度最小的前缀编码称为最优编码,可以通过构造huffman树解决,Huffman树的带权路径长度就是相应编码的平均编码长度,得到的编码称为Huffman编码。
double weight[LEAF_NUM] = {0.05, 0.1, 0.1, 0.05, 0.3, 0.1, 0.1, 0.1, 0.05, 0.05};
DataType val[LEAF_NUM * 2 - 1] = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j'};
a:0110
b:1110
c:1111
d:0111
e:10
f:000
g:001
h:010
i:1100
j:1101
averageCodingLength is:3.1性质:
-
每个结点都有作为查找依据的关键码(key),所有结点的关键码互不相同(简化);
-
非空左子树上所有结点的关键码都小于根结点的关键码;
-
非空右子树上所有结点的关键码都大于根结点的关键码;
-
左子树和右子树也是二叉搜索树;
-
中序遍历时各结点的关键码按从小到大的顺序排列。
-
微观上处处满足顺序性
-
整体上满足单调性
-
为提高算法可读性一般不设关键码项,直接用数据值进行比较,相当于有限制的二叉树;
//验证二叉搜索树
//算法1
long long pre = LLONG_MIN;//要比所有int小,保证第一次的比较恒成立
bool isValidBST(TreeNode *root)
{ //中序遍历
if (!root)
return true;
if (!isValidBST(root->left))
return false;
if (root->val <= pre) //二叉搜索树「中序遍历」得到的值构成的序列一定是升序的
return false;
pre = root->val;
if (!isValidBST(root->right))
return false;
return true;
}
//算法2
bool isValidBST(TreeNode *root)
{
return isValid(root, NULL, NULL); //使用指针可以避免边界值的影响,NULL替代绝对的最值,保证最初的比较
}
bool isValid(TreeNode *root, int *lower, int *upper)//自底向上保证结点值在low和upper范围内
{
if (!root)
return true;
if (upper && root->val >= *upper)
return false;
if (lower && root->val <= *lower)
return false;
return isValid(root->left, lower, &(root->val)) && isValid(root->right, &(root->val), upper);
}查找的行为类似与二分查找,查找的比较次数不超过高度h,最好logn,最坏n;
查找算法决定了能否进行插入删除操作并提供了进行插入删除时所需的目标位置的位置信息(父节点)。
删除操作在目标结点有左右子女的情况下复杂度最高,但也是O(h);
bool deleteBSNode(BSTree root, BSTDataType x)
{
BSTree father, cur, p;
if (!(cur = search(root, x, father)))
return false;
if (cur->lchild && cur->rchild) //寻找中序直接后继(右子树里的最左端),并对调数据,使情况归于travial,father记录父结点
{
p = cur->rchild;
father = cur;
while (p->lchild)
{
father = p;
p = p->lchild;
}
cur->data=p->data;//更换被删节点原位置的值为其后继的值,注意不能改变p的值,因为最后要判别方向
cur = p;//将cur移到待删处
}
p = cur->lchild ? cur->lchild : cur->rchild; //p为将要被链接的结点,cur至多有一个子树
if (!father) //被删的为根结点
root = p;
else //p是否存在都要链接,不存在时父节点要置空
cur->data < father->data ? father->lchild = p : father->rchild = p;
delete cur;
cur=nullptr;
return true;
}二叉搜索树的性能分析
固定中序序列可构成的不同二叉搜索树的个数为卡特兰数,可以用树的平均查找长度来衡量它们 。
中序序列相同而拓扑结构不同的二叉树为一个等价类
将原二叉搜索树的结点结点看做内结点,扩充得到扩充二叉树;
内结点树为n时,外结点树为n+1;用I表示所有内结点的路径长度之和,E表示所有外结点的路径长度之和,则有$E=I+2n$, 每个内结点为外结点贡献两个单位路径长度(左子树一个,右子树一个)。
对扩充二叉树进行中序遍历的结果中内结点与外结点交替排列,每个内结点都在两个外结点之间。
定义查找成功的平均查找长度为$ASL_{成功}=\sum_{i=1}^np[i]l[i]$,L[i]是第i个内结点的层次号,等于找到该结点的关键码比较次数,p[i]为结点查找概率;
查找不成功的平均查找长度为$ASL_{不成功}=\sum_{i=0}^nqj$,$l'[j]$为外结点层次号,减一为关键码平均比较次数。
所有结点的概率之和为1,两个公式之和即为扩充二叉树的平均查找长度ASL
各结点概率不相等情形下类似Huffman树,区别是还要计算内结点概率
相等查找概率情形下高度最小的扩充二叉树的平均查找长度最短,称为最优二叉搜索树,其平均查找长度公式为
随机情况下二叉搜索树的查插删操作的平均时间复杂度为$O(\log_2n)$
AVL树是一种高度平衡二叉树(BBST);
定义:所有结点的左子树和右子树的高度之差的绝对值不超过1
平衡因子(balence factor):左子树高度减去右子树高度
struct AVLNode
{
AVLDataType data;
AVLNode *lchild, *rchild, *parent;
int height; //此信息更为有用,替代需要通过高度计算的平衡因子,初高为1
AVLNode(AVLDataType _data = 0, AVLNode *_parent = nullptr, AVLNode *_lchild = nullptr, AVLNode *_rchild = nullptr, int _height = 1) : data(_data), parent(_parent), lchild(_lchild), rchild(_rchild), height(_height) {}
};
using AVLTree = AVLNode *;插入操作:
插入一个结点,其所有祖先都有可能会失衡
平衡化旋转:从插入位置向上回溯直到发现不平衡的结点,从发生不平衡的结点起,沿回溯的路径取下两层的结点(沿高度更高的子树路径),如果这3个结点位于同一条直线上,则采用单旋转进行平衡化,否则用双旋转;
单旋转分为左单旋转和右单旋转
左单旋转又称RR旋转(根据三个结点向下的路径,与其名称中的左相反),用于在结点的右子树的右子树上插入新结点导致不平衡的情况,具体是回溯找到不平衡结点(此结点原本的平衡因子为-1,插入的结点使其变为-2,此子树称为最小不平衡子树),考虑两个结点,以此结点的右子女为旋转轴逆时针旋转使此结点成为其右子女的左子女,并使原来右子女的左子女成为此结点的右子女,使子树的高度恢复插入前的状态;
对称可得右单旋转(LL旋转)的定义(最小不平衡子树的平衡因子因插入从1变为2,通过旋转使其恢复1)
双旋转分为先左后右旋转(LR)和先右后左(RL)旋转(与名称方向一致);
先左后右旋转(不平衡结点的平衡因子为1,在其左子树的右子树上插入结点导致平衡因子变为2),考虑三个结点,具体是以最下层的结点为旋转轴先进行一次左单旋转将其双亲结点(中间位置的结点)旋转下去,再进行一次右旋转将其新的双亲结点(最上层的结点)旋转下去;
对称可得先右后左旋转的定义;
插入具体算法:
-
调用普通BST的插入函数获取父结点(插入函数较简单,且普通插入函数可能没有链接父结点的功能,故可以直接实现) 为空即返回
-
从新插入结点的双亲开始向上回溯
-
bf=0/1/-1:依然平衡,不做额外操作,继续回溯;
-
bf=2/-2:
-- bf=2:若左子女的bf也为正进行LL旋转,否则进行LR旋转;
-- bf=-2;若右子女的bf也为负进行RR旋转,否则进行RL旋转。
-- 具体实现可以从此结点沿更高的子树向下行进两层,将该节点传入平衡操作函数,操作函数可根据此结点找到其父结点 与祖父结点,进而根据它们的关系进行旋转
-
若不需要进行平衡操作则更新结点的高度并继续回溯
-
最小不平衡子树高度恢复,祖先状态自动恢复,无须继续回溯。
3+4重构:我们设g(x)为最低的失衡结点,考察祖孙三代:gpv,按照中序遍历次序将其重命名为:a<b<c。
它们总共拥有互不相交的四颗(可能为空的)子树,按照中序遍历次序,将其重命名为:T0<T1<T2<T3。
此时,如果我们依然按照中序的遍历次序将这两个序列混合起来,就可以得到一个长度为7的序列。在这个序列中三个结点a,b,c,必然是镶嵌于这4棵子树之间
只要按顺序传入三个结点及四个对应的子树就可用通用的算法重构得到平衡的AVL树。
bool insert(AVLTree &root, AVLDataType x)
{
AVLTree cur, father;
if (search(root, x, father))
return false;
cur = new AVLNode(x, father); //注意与父结点链接
if (isRoot(cur)) //空树则将当前结点作为根
root = cur;
else
x < father->data ? father->lchild = cur : father->rchild = cur;
for (AVLTree p = father; p; p = p->parent) //平衡化
{
if (abs(getHeight(p->lchild) - getHeight(p->rchild)) >= 2)
{ //p的父结点与旋转后的子树链接,根结点直接修改
if (isRoot(p))
root = rotate(tallerChild(tallerChild(p)));
else
{ //旋转会修改p,需要保存其父结点
AVLTree par = p->parent;
isLchild(p) ? par->lchild = rotate(tallerChild(tallerChild(p))) : par->rchild = rotate(tallerChild(tallerChild(p)));
}
break; //旋转后即可退出
}
else
updateHeight(p); //更新回溯路径上的高度
}
return true;
}
AVLTree rotate(AVLTree v)
{
if (!v)
exit(1);
AVLTree p = v->parent, g = p->parent; //父结点和祖父节点
//判断类型,按中序序列传入参数
if (isLchild(p))
{
if (isLchild(v)) //LL
{
p->parent = g->parent; //顶部交接
return connect34(v, p, g, v->lchild, v->rchild, p->rchild, g->rchild);
}
else //LR
{
v->parent = g->parent;
return connect34(p, v, g, p->lchild, v->lchild, v->rchild, g->rchild);
}
}
else
{
if (isRchild(v)) //RR
{
p->parent = g->parent;
return connect34(g, p, v, g->lchild, p->lchild, v->lchild, v->rchild);
}
else //RL
{
v->parent = g->parent;
return connect34(g, v, p, g->lchild, v->lchild, v->rchild, p->rchild);
}
}
}
AVLTree connect34(AVLTree a, AVLTree b, AVLTree c, AVLTree T0, AVLTree T1, AVLTree T2, AVLTree T3)
{
//注意更新高度
a->lchild = T0;
if (T0)
T0->parent = a;
a->rchild = T1;
if (T1)
T1->parent = a;
updateHeight(a);
c->lchild = T2;
if (T2)
T2->parent = c;
c->rchild = T3;
if (T3)
T3->parent = c;
updateHeight(c);
b->lchild = a;
a->parent = b;
b->rchild = c;
c->parent = b;
updateHeight(b);
return b;
}删除操作:
删除一个结点会可能导致一个子树失衡,但复衡的后子树高度如果降低可能会导致其祖先的失衡,开销较插入更大
具体算法:
-
调用普通的BST删除,获取目标位置父结点,为空则返回
-
然后进行复衡与更新高度直到根结点
-
旋转类型类似插入时,使用3+4重构更为简洁
bool remove(AVLTree &root, AVLDataType x)
{
if (!root)
return false;
AVLTree p = deleteNode(root, x); //获取被删结点的父结点
if (!root) //删除的为根结点
return true;
if (!p) //删除失败
return false;
while (p)
{
if (abs(getHeight(p->lchild) - getHeight(p->rchild)) >= 2)
{
if (isRoot(p))
p = root = rotate(tallerChild(tallerChild(p)));
else
{
AVLTree par;
par = p->parent;
p = isLchild(p) ? par->lchild = rotate(tallerChild(tallerChild(p))) : par->rchild = rotate(tallerChild(tallerChild(p)));
}
}
updateHeight(p); //需做O(logn)次调整,极端情况是每次上溯都要调整,无论是否做过调整,树高度均可能降低
p = p->parent;
}
return true;
}性能分析
设$N_h$是高度为h的AVL树的最小结点树,根据平衡条件,在最差情况下,根的一棵子树的高度为h-1,另一棵的高度为h-2,这两个子树也是高度平衡的,因此有$N_0=0,N_1=1$,$N_h=N_{h-1}+N_{h-2}+1,h>1$.
对于$h\geq1,有N_h=F_{n+2}-1$,经过推导可得,$h<1.44\log_2(N_h+2)-0.327$
所以AVL树的最大高度相当于斐波那契树的情形,最小高度相当于完全二叉树的情形
优点:
各种操作的时间复杂度最坏是O(logn),空间复杂度为O(n);
缺点:
需借助高度或平衡因子,需要改造或额外封装数据元素
插删操作特别是删除操作成本不菲
单次动态调整后,全树拓扑结构的变化量可能高达O(logn);
//利用递归实现回溯,类似通配符匹配
class Solution
{
public:
vector<vector<string>> solveNQueens(int n)
{
vector<string> chess(n, string(n, '.'));
vector<vector<string>> ans;
helper(chess, ans, 0, n);
return ans;
}
private:
void helper(vector<string> chess, vector<vector<string>> &ans, int k, int n)
{
bool attack;
if (k <= n)
{
for (int i = 0; i < n; i++)
{
chess[k][i] = 'Q'; //放置皇后
attack = false;
for (int j = 0; j < k; j++) //与前k-1行比较判断是否被攻击
if (chess[k] == chess[j] || abs(k - j) == abs((int)chess[j].find_first_of('Q') - (int)chess[k].find_first_of('Q')))
{
attack = true;
break;
}
if (attack == false)
if (k == n-1)//!
ans.emplace_back(chess);
else
{
helper(chess, ans, k + 1, n);
}
chess[k][i] = '.'; //复位本行棋盘,选择下一列
}
}
}
};
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]定义在集合A上的关系叫做等价关系,如果它是自反的,对称的和传递的。
设R是定义在集合A上的等价关系,与A中的一个元素a有关系的所有元素的集合叫做a的等价类。代表元为a的A上的关于R的等价类记作$[a]_R$,只考虑一个关系时可省去下标。
模m同余关系的等价类叫作模m同余类,整数a的模m同余类满足$[a]_m={\cdots,a-2m,a-m,a,a+m,a+2m,\cdots}$
设R是定义在集合A上的等价关系,下面的关于集合A中a,b两个元素的命题是等价的:
-
aRb
-
$[a]=[b]$ -
$[a]\cap[b]=\varnothing$
等价类构成一个划分(非空,无交,覆盖)
由等价类可以得到一个划分(将划分中的每一个子集作为一个等价类),由一个划分也可以得到一个等价类(讲一个等价类(通常是一组有序对)中有关系的有序对中的元素作为划分子集)
A={1,2,3,4},由等价关系R={(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),(4,4)}得到的一个划分为P1={1,2,3},P2={4};因为R(1)=R(2)=R(3)={1,2,3},R(4)={4};
以余数相等作为等价关系可得到m个不同的模m同余类,它们构成了整数集合的划分
集合上的等价关系数等于划分数
含有n个元素的集合的划分数$S(n)=\sum_{i=1}^nS(n,k),S(n,k)$表示将集合划分为k个子集的划分数
不能把n个元素不放进任何一个集合中去,即k=0时,S(n,k)=0;也不可能在不允许空盒的情况下把n个元素放进多于n的k个集合中去,即k>n时,S(n,k)=0;再者,把n个元素放进一个集合或把n个元素放进n个集合,方案数显然都是1。
对于任一个元素an,则必然出现以下两种情况:
1.{an}是k个子集中的一个,于是我们只要把a1,a2,......,an-1划分为k-1个子集,便解决了本题,这种情况下的划分数共有S(n-1,k-1)个; 2.{an}不是k个子集中的一个,则an必与其他的元素构成一个子集。则问题相当于先把a1,a2,......,an-1划分成k个子集,这种情况下划分数共有S(n-1,k);然后再把元素an加入到k个子集中的任一个中去,共有k中加入方式,这样对于an的每一种加入方式,都可以使集合划分为k个子集,因此根据乘法原理,划分数共有k*S(n-1,k)个。
并查集(UnionFindSet)
struct UFSets
{
private:
vector<int> fa;
Timer timer;
public:
size_t size() { return fa.size(); }
UFSets(size_t size = SIZE)
{
fa.assign(size, -1); //初始各成一派,都是集合(根),fa[root]的相反数为其集合中元素个数
}
size_t find(size_t x) //查找根(等价类代表元),同时实现路径压缩,将沿途结点指向根结点,减少重复查找所需时间
{
return fa[x] < 0 ? x : (fa[x] = find(fa[x]));
}
void merge(size_t x, size_t y) //合并在元素较多集合上,防止树发生退化(高度过高)
{
if (x != y)
{
int setx = find(x), sety = find(y); //找到所属集合
int sum = fa[setx] + fa[sety];
//根结点fa为负值,越小元素数越多
fa[setx] < fa[sety] ? (fa[sety] = setx, fa[setx] = sum) : (fa[setx] = sety, fa[sety] = sum);
}
}
void initByOrderedPair(vector<pair<int, int>> &pairs) //通过有序关系对初始化
{
for (int i = 0; i < pairs.size(); i++)
merge(pairs[i].first, pairs[i].second);
}
vector<string> divide() //划分获得等价类
{
vector<string> result;
string set;
for (size_t i = 0; i < fa.size(); i++)
{
if (fa[i] < 0)
{
for (int j = 0; j < fa.size(); j++)
{
if (find(j) == i) //将满足等价关系的元素放进字符串(不是所有路径都压缩过,不能直接用父亲判断)
set += to_string(j) + ",";
}
set.pop_back(); //吐出最后一个逗号
result.emplace_back(set);
set.clear();
}
}
return result;
}
/*
size_t find(size_t x)
{
while (fa[x] >= 0)
x = fa[x];
return x;
}
void merge(size_t x, size_t y) //合并在x根上
{
if (x != y)
fa[x] += fa[y];
fa[y] = x; //y指向x
}*/
};查找操作的复杂度不超过树高(logn),合并复杂度取决于查找;在一定范围内查找次数越多被压缩的路径越多复杂度越低
1,递归,dfs,在某个路口分为取和舍两路
2,求(0,1)向量的n(元素个数)次笛卡尔积,所得的序列对应每个元素的取舍,可以循环,也可以用法1求笛卡尔积序列。
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
void getPower(vector<string> &loc, string res, vector<int> set, size_t index)
{
if (index == set.size())
{
if (res.back() == ',')
res.pop_back();
res += "]";
loc.emplace_back(res);
return;
}
getPower(loc, res, set, index + 1); //不选
res += to_string(set[index]) + ','; //选
getPower(loc, res, set, index + 1);
}
vector<string> cartesianProduct(vector<string> setx, vector<string> sety) //求两个集合的笛卡尔积,元素类型为string
{
vector<string> ans(setx.size() * sety.size());
size_t t = 0;
for (auto x : setx)
for (auto y : sety)
ans[t++] += (x + y);
return ans;
}
vector<string> cartesianProduct(vector<string> set, int n) //就一个集合的笛卡尔幂
{
vector<string> ans = set;
ans.reserve(pow(set.size(), n));
n--;
while (n--) //作n-1次笛卡尔积
ans = cartesianProduct(ans, set);
return ans;
}
int main()
{
vector<int> set = {1, 2, 3};
vector<string> loc;
loc.reserve(pow(2, set.size()));
string res{"["};
getPower(loc, res, set, 0);
for (auto i : loc)
cout << i << endl;
cout << endl;
vector<string> Set = {"0", "1"}, ans(pow(2, set.size()));
ans = cartesianProduct(Set, set.size());
for (auto i : ans)
cout << i << endl;
cout << endl;
for (auto i : ans)
{
for (size_t j = 0; j < set.size(); j++)
if (i[j] - '0')
cout << set[j];
cout << endl;
}
}
运行结果:
[]
[3]
[2]
[2,3]
[1]
[1,3]
[1,2]
[1,2,3]
000
001
010
011
100
101
110
111
3
2
23
1
13
12
123G(V,E):G:图名,V:点集,G:边集
| 类型 | 边 | 允许多重边 | 允许环 |
|---|---|---|---|
| 简单图 | 无向 | 否 | 否 |
| 多重图 | 无向 | 是 | 否 |
| 伪图(基本无向图) | 无向 | 是 | 是 |
| 有向简单图 | 有向 | 否 | 否 |
| 有向多重图 | 有向 | 是 | 是 |
| 混合图 | 有向和无向 | 是 | 是 |
握手定理:
-
无向图:$2m=\sum_{v\in V}deg(v)$
-
有向图:$\sum_{v\in V}deg^-(v)=\sum_{v\in V}deg^+(v)=|E|$
无向图有偶数个度为奇数的结点,即奇顶点总是成对出现
几类简单图:完全图$K_n$,圈图$C_n(n\geq 3)$,轮图$W_n$:圈图添加一个顶点和若干边而成,n立方体图$Q_n$:用顶点表示$2^n$个长度为n的位串的图。
无向完全图有$\sum_{i=0}^{n-1}=\frac{n(n-1)}{2}$条边,乘二即为有向完全图的边数
二分图:图的顶点分为两个不相交的子集,每条边连接不同子集的顶点,一个简单图是二分图当且仅当能够对图中的每对顶点赋予不同的颜色并使得没有两个相邻的顶点被赋予同一种颜色,此时两种颜色的顶点对应两个集合,任意两个不同子集的顶点都邻接时为完全二分图$K_{m,n}$
匹配:在简单集G(V,E)中的一个匹配M就是边集E的子集,且该子集中没有两条边关联了相同的顶点;包含最多边数的匹配称为最大匹配
在二分图中,若|M|=|V1|,则称M(边集合)是从V1到V2的完全匹配,此时必然有|V1|<=|N(V1)|=|V2|,V1的任意子集A也满足,即|N(A)|>=|A|(N(A)表示A的邻接顶点集合),即为霍尔婚姻定理,是存在完全匹配的充要条件
导出子图:包含子图顶点在原图中的所有对应边的子图
并图,补图类似并集补集
邻接矩阵表示,类似于关系矩阵,简单图的邻接矩阵是对称的(无向),并且主对角线上元素都为0(没有环),当为带权图时则将没有关系的位置设为一个max值(也可以规定权值大于0,将没有关系设为0),有邻接的顶点对应位置即为权值,邻接矩阵也可以表示带环和多重边的图的有向图,元素表示对应顶点间的边数
本质是边组成的矩阵,可以用元素为边对象指针的矩阵实现,指针为空即为没有关系
对于无向图,第i行或第i列元素之和为顶点i的deg
对于有向图,第i行元素之和是顶点i的indeg,第j列元素之和为顶点j的outdeg.
当含有的边数少于超过所有可能的边数的一半时适合用邻接矩阵,否则过于稀疏时适合用邻接表,前者判断边的存在只需一次比较,而后者需要O(|V|)次比较
关联矩阵:横坐标为边,纵坐标为顶点,便于表示多重边和环的无向图
连通关系是一个顶点集合上的等价关系,将顶点划分为等价类,称为连通分支(连通子图)
两个顶点间有路径则称两个顶点是连通的,如果图中任意一对顶点都是连通的则称此图是连通图,连通无向图的每一对顶点之间都有简单通路(无重复边),非连通图的极大连通子图叫做连通分量,连通图只有它本身一个连通分支。
没有重复点的通路为初级通路,初级通路一定是简单通路 。
不连通的图有两个或两个以上不相交的连通子图
有向图中若每对顶点间都有互相到达的路径,则称此图为强连通图,其极大连通子图为强连通分量,去掉有向性后如果是连通图则为弱连通图
删除割点(关节点)或割边(桥)就会产生更多的连通子图(改变连通性),在计算机网络的图中它们分别表示最重要的路由器和最重要的链路
删除任意一个结点依然连通的图不含割点,称为不可分割图,比有割点的连通图具有更好的连通性
非完全图的点连通度为点割即中最小的顶点数(使图不连通所需的最少顶点数),记作k(G),连通图的点连通度定义为n-1,即使连通图变为只含有一个顶点。k(G)越大,连通性越好,不连通图的k(G)为0
类似可得边连通度的定义
点连通度小于等于边连通度小于等于图中最小的度
max(min[u,v])叫做图的直径,就是最长的距离,不存在通路时距离定义为无穷
生成树:一个无向连通图的生成树是它的包含每个顶点的极小连通子图
一个无向连通图至少有n-1条边,若刚好有n-1条边时即为生成树
图的同构:设G1=(V1,E1)和G2=(V2,E2)是简单图,若存在双射f使得a和b在G1中相邻当且仅当f(a)和f(b)在图G2中相邻。
顶点数,边数和顶点的度还有特定长度简单回路都是在同构下的不变量(必要条件),但没有已知的用来判断简单图是否同构的不变量集,度为3的顶点和连接它们的边所构成的子图一定是同构的
若$A_G=A_H$,其中前者是G的邻接矩阵,后者是H上由G的对应顶点的像标记行和列的矩阵,则f是保持边的,由此得出f是同构,但不能通过f不是同构得到两个图不同构,因为两个图的顶点的另一个对应关系可能同构
沿着经过所有结点并且使得两个图的对应顶点的度都相同的通路前进,可以构造可能的同构,这个过程可以保证它们的邻接矩阵是相同的
根据邻接矩阵计算通路数:
从$v_i$到$v_j$的长度为r的通路数等于$A^r$的第(i,j)项
可以用来求两点间的最短通路数(对应位置第一次非零时的值)
可达矩阵M=$(A+I)^n=I+A+A^[2]+A^[3]+\dots+A^[n]$ 是0次幂(I:添加自反性)到n次幂(长度为n的路径)的并,由于自反性已经添加,故到n-1次即可,可以用布尔幂,也可以用普通幂然后将结果中的非零元素归1,即为图中邻接关系(A+I)的传递闭包。将Warshall算法的结构与单位阵进行布尔或即为所得
访问数据域是访问的一部分
BFS
template <typename Tv, typename Te>
void Graph<Tv, Te>::bfs(int s)
{
reset();
int v = s;
int clock = 0;
do//遍历每个不重复的连通域
{
if (status(v) == UNDISCOVERED)
BFS(v, clock);
} while (s != (v = (++v % n)));
}
void Graph<Tv, Te>::BFS(int v, int &clock, vector<Tv> &path)
{
std::queue<int> Q;
status(v) = DISCOVERED;
dTime(v)=++clock;
Q.push(v);
while (!Q.empty())
{
int v = Q.front();
Q.pop();
path.emplace_back(vertex(v));//访问数据域
for (int u = firstNbr(v); u > -1; u = nextNbr(v, u))
{
if (status(u) == UNDISCOVERED)
{
status(u) = DISCOVERED;
dTime(v) = ++clock; //标记每个顶点被探测的时间(顺序)
Q.push(u);
type(v, u) = TREE; //引入树边支撑拓展树
parent(u) = v;
}
else
type(v, u) = CROSS; //归于跨边(v已被访问或发现)
}
status(v) = VISITED; //v被访问完毕
//访问结束时间fTime与Dtime等价
}
}连通的无向图一次搜索就可以覆盖全图,有向图查找次数与顶点选取有关
复杂度:邻接表:O(n+e),邻接矩阵O(n^2),考虑到结点数组大概率存储在高速缓存区,实际与邻接表存储的复杂度一致
是树的层序遍历的拓展,所生成的支撑树中的顶点到初始顶点的路径即为两顶点之间的最短路径
DFS
template <typename Tv, typename Te>
void Graph<Tv, Te>::dfs(int s, vector<Tv> &path)
{
reset();
int clock = 0;
int v = s;
do
{
if (status(v) == UNDISCOVERED)
DFS(v, clock, path);
} while (s != (v = (++v % n)));
}
template <typename Tv, typename Te>
void Graph<Tv, Te>::DFS(int v, int &clock, vector<Tv> &path)
{
dTime(v) = ++clock;
status(v) = DISCOVERED;
path.emplace_back(vertex(v));//访问数据域
for (int u = firstNbr(v); u > -1; u = nextNbr(v, u))
{
switch (status(u))
{
case UNDISCOVERED: //u尚未发现,意味着支撑树可在此拓展
type(v, u) = TREE;
parent(u) = v;
DFS(u, clock, path);
break;
case DISCOVERED: //u已被发现但尚未访问完毕,应属被后代指向的祖先
type(v, u) = BACKWARD;//每一条BACKWARD的边都代表着一个环(loop)的存在
break;
default: //u已访问完毕(VISITED,有向图),则视承袭关系分为前向边(在当前顶点之后是非子女的后代)
//或跨边(在当前顶点之前是表亲)
type(v, u) = (dTime(v) < dTime(u)) ? FORWARD : CROSS;
}
}
status(v) = VISITED;//至此,当前顶点v方告访问完毕
fTime(v) = ++clock;//访问完毕时间
}是树的先序遍历的拓展
括号引理
Parenthesis Lemma:给定有向图G(V,E)及其任意DFS森林,则
$\begin{cases} u是v的祖先->active[u]\supseteq active[v]\ u是v的子女->active[u]\subseteq active[v]\ u和v没有直系亲属关系-> active[u]\cap active[v]=\varnothing \end{cases} $
通过这样可以用O(1)的复杂度判断两个顶底是否有直系亲属关系,通过parent域判断需要O(n)的复杂度
构造一个相容的偏序,某个顶点(除最小元)被访问当且仅当小于它的顶点都已被访问
零入度算法:每一步选择极小元(零入度,根)加入结果并删除此顶点,缺点是需要大量的比较和删除操作,复杂度较高,当然实际上可以通过维护一个入度数组和极小元栈实现
零出度算法:进行全图的DFS遍历,当顶点是极大元(零出度,叶)或后序顶点都已被访问时(如果删除被访问的顶点,就相当于极大元)顶点进入排序序列(入栈),出栈的结果即为拓扑排序的序列,即为各顶点回溯顺序的倒序,亦位DFS算法退出递归时输出当前顶点的值所得到的序列用后序顶点都已被访问作为特征可知fTime越靠后,在拓扑排序中越靠前,fTime从大到小的排列即为结果,这样可以不用修改或重写原DFS(实际做题需要重写改进,可依据backtrack的出现(探测但未访问)证明有环,并在遍历过程中记录回溯顶点),易知如果遍历起始点为最小元则只须遍历一次
拓扑排序不能排序带环的图(格),而用DFS可以得到结果,但结果不合理,与选取的顶点有关,需要在探测到环时退出排序
void TopologicalSort(vector<Tv> &order) //传入DAG图dfs排序后的序列(或是任意的顶点标签值序列,都要确保先进行dfs),不能辨别带环的图
{
std::sort(order.begin(), order.end(), [&](Tv a, Tv b)
{ return fTime(loc(a)) > fTime(loc(b)); }); //按fTime逆序排列
}判断是否有环
class Solution
{
public:
bool canFinish(int numCourses, vector<vector<int>> &prerequisites)
{
neighbors.resize(numCourses);
visited.resize(numCourses);
visited.assign(numCourses, 0);
for (int i = 0; i < prerequisites.size(); i++)
neighbors[prerequisites[i][1]].emplace_back(prerequisites[i][0]);
flag = true;
for (int v = 0; flag && v < numCourses; v++)
if (!visited[v])
dfs(v);
return flag;
}
vector<vector<int>> neighbors;
vector<int> visited;
bool flag;
void dfs(int v)
{
if (!flag) //终止
return;
visited[v] = 1; //探测
for (auto i = neighbors[v].begin(); i != neighbors[v].end(); i++)
{
if (!visited[*i])
dfs(*i);
else if (visited[*i] == 1) //探测到但未访问完毕是一个回边,代表一个有向环的存在
flag = false;
}
visited[v] = 2; //访问完毕
}
};当无向图为连通图时,从某一顶点出发进行DFS所能访问到的所有顶点构成一个连通分量,从所有未被访问顶点出发进行DFS即可得到无向图的所有连通分量 ,连通分量构成一组等价类,所以也可以利用并查集进行计算
去除任一顶点后图任能保持连通的无向图称为双连通图(双向连通图),任意两个顶点之间存在到达对方的不重合的路径,非双连通图包含多个双连通分量(Biconnected Components)
双连通分量之间通过关节点连接
判断关节点的准则
-
根结点若至少有两个子女则一定是关节点(无向图不会有跨边)
-
叶节点不是关节点(去除不会影响连通状态)
-
内部顶点不是关节点当且仅当它的任一子孙都可以绕过它到达u的某一祖先,而且u不属于这条路径
有向图的强连通分量类似无向图的双连通分量,可以依据上述的第三条准则为原理的tarjana算法得到强连通分量(strongly connected component (SCC)),也可以得到无向图的双连通分量
tarjan算法计算bcc
template <typename Tv, typename Te>
void Graph<Tv, Te>::bcc()
{
if (direct == DIRECTED)
{
cout << "please try scc or scc2" << std::endl;
return;
}
reset();
int v = 0;
int clock = 0;
stack<int> S;
while (v != n - 1)
{
if (status(v) == UNDISCOVERED)
{
BCC(v, clock, S);
S.pop(); //*遍历返回后,弹出栈中最后一个顶点——当前连通域的起点
}
v++;
}
}
#define hca(x) (fTime(x)) //利用闲置的fTime()充当hca(),highest connnected ancestor
template <typename Tv, typename Te> //顶点类型、边类型
void Graph<Tv, Te>::BCC(int v, int &clock, stack<int> &S)
{
hca(v) = dTime(v) = ++clock; //初始的hca是探测时间
status(v) = DISCOVERED;
S.push(v);
for (int u = firstNbr(v); - 1 < u; u = nextNbr(v, u))
switch (status(u))
{ //视u的状态分别处理
case UNDISCOVERED:
parent(u) = v;
type(v, u) = TREE;
BCC(u, clock, S); //从顶点u处深入
if (hca(v) > hca(u))
hca(v) = std::min(hca(v), hca(u)); //更新hca[v]
else //子女的hca不可能大于祖先
{ //*弹出当前BCC中(除关节点v外)的所有节点,v可能是其它连通域的成员,不能退栈
cout << vertex(v);//输出关节点
while (S.top() != u)//*v,u在栈中不一定连续,要用u作为终止条件
{
cout << vertex(S.top());
S.pop();
}
cout << vertex(S.top()) << std::endl;
S.pop();
}
break;
case DISCOVERED:
type(v, u) = BACKWARD;
hca(v) = std::min(hca(v), dTime(u)); //更新hca[v]
break;
default: //VISITED (有向图),与本算法无关
type(v, u) = (dTime(v) < dTime(u)) ? FORWARD : CROSS;
break;
}
status(v) = VISITED;
}
#undef hca
tarjan算法计算scc
template <typename Tv, typename Te>
void Graph<Tv, Te>::scc()
{
if (direct == UNDIRECTED)
{
cout << "please try dcc" << std::endl;
return;
}
reset();
int v = 0;
int clock = 0;
stack<int> S;
while (v != n - 1)
{
if (status(v) == UNDISCOVERED)
SCC(v, clock, S);
v++;
}
}
#define hca(x) (fTime(x)) //利用闲置的fTime()充当hca(),highest connnected ancestor
template <typename Tv, typename Te> //顶点类型、边类型
void Graph<Tv, Te>::SCC(int v, int &clock, stack<int> &S)
{
hca(v) = dTime(v) = ++clock; //初始的hca是探测时间
status(v) = DISCOVERED;
S.push(v);
for (int u = firstNbr(v); - 1 < u; u = nextNbr(v, u))
switch (status(u))
{ //视u的状态分别处理
case UNDISCOVERED:
parent(u) = v;
type(v, u) = TREE;
SCC(u, clock, S); //从顶点u处深入
hca(v) = std::min(hca(v), hca(u)); //更新hca[v]
break;
case DISCOVERED: //在栈中
type(v, u) = BACKWARD;
hca(v) = std::min(hca(v), dTime(u)); //更新hca[v]
break;
default: //VISITED (有向图),与本算法无关
type(v, u) = (dTime(v) < dTime(u)) ? FORWARD : CROSS;
break;
}
if (hca(v) == dTime(v))
{ //输出一个SCC
//*弹出当前SCC中(包括桥结点v)的所有节点
while (v != S.top())
{
cout << vertex(S.top());
status(S.top()) = VISITED; //出栈输出宣告访问结束
S.pop();
}
if (direct == DIRECTED) //v是桥的顶点,归于本强连通域,需要出栈
{
cout << vertex(S.top()); //输出v
status(S.top()) = VISITED;
S.pop();
}
cout << std::endl;
}
}
#undef hca
Kosaraju算法计算scc
按顶点回溯顺序的逆序对原图的反向图进行BFS
template <typename Tv, typename Te>
template <typename T>
void Graph<Tv, Te>::scc2()
{
if (direct == UNDIRECTED)
{
cout << "please try dcc" << std::endl;
return;
}
vector<Tv> path;
path.reserve(n);
dfs(0, path);
vector<int> order(n);
for (int i = 0; i < n; i++)
order[i] = i;
std::sort(order.begin(), order.end(), [&](int i, int j) //获得回溯序列的逆序
{ return fTime(i) > fTime(j); });
T *G = getRevese<T>();
for (int i = 0, clock = 0; i < this->n; i++)
{
if (G->status(i) == UNDISCOVERED)
{
path.clear();
G->DFS(order[i], clock, path);
for (auto i : path)
cout << i;
cout << std::endl;
}
}
delete G;
}
框架
template <typename Tv, typename Te>
template <typename PU>
void Graph<Tv, Te>::pfs(int s, PU prioUpdater)
{
reset();
int v = s;
do
{
if (UNDISCOVERED == status(v))
PFS(v, prioUpdater);
} while (s != (v = (++v % n)));
}
template <typename Tv, typename Te>
template <typename PU>
void Graph<Tv, Te>::PFS(int v, PU prioUpdater, Graph<Tv, Te> &SPTree)
{
//图中顶点初始优先级为INT_MAX
priority(v) = 0; //初始化源顶点
parent(v) = -1;
IndexMinPQ Q(n); //创建容量为n的下标优先队列
Q.enqueue(v, priority(v));
while (!Q.empty())
{
v = Q.dequeue();
for (int w = firstNbr(v); w > -1; w = nextNbr(v, w)) //更新在剩余集合中当前顶点邻居的优先级
if (status(w) == UNDISCOVERED)
{
prioUpdater(this, v, w);
if (Q.exists(w)) //更新队列
Q.change(w, priority(w));
else
Q.enqueue(w, priority(w));
}
status(v) = VISITED; //更新选中的新的顶点和相关的边
int prt = parent(v);
if (prt != -1) //排除源点
{
type(prt, v) = TREE; //标记原树在生成树对应的边
SPTree.insert(prt, v, weight(prt, v), (Te)1); //生成树和原图顶点的下标相同
SPTree.parent(v) = prt;
}
}
}前一个循环对于邻接矩阵复杂度是n^2,对于邻接表是n+e,后一层对于两者都是n^2,用优先级队列以上两项将可达到elogn和nlogn,合计为(n+e)logn,
最小生成树算法
Prim:
template <typename Tv, typename Te>
void Graph<Tv, Te>::prim(int s, Graph<Tv, Te> &SPTree)
{
reset();
auto primPU = [](Graph<Tv, Te> *g, int v, int w)
{
if (g->priority(w) > g->weight(v, w))
{
g->priority(w) = g->weight(v, w);
g->parent(w) = v;
}
};
SPTree.direct = this->direct;
for (int i = 0; i < this->n; i++) //初始化顶点
SPTree.insert(i);
PFS(s, primPU, SPTree);
}复杂度
普通优先队列:时间:ElogE,空间:E
下标优先队列:时间:ElogV,空间:V(主要优势)
区别在于队列的状态,前者无效边会保留在队列,而后者会进行筛选,且判断是否已经存在与队列(堆)的语句复杂度为1
Dilkstra算法,所得路径是最短路径
template <typename Tv, typename Te>
void Graph<Tv, Te>::dijkstra(int s)
{
reset();
auto DijkPU = [](Graph<Tv, Te> *g, int v, int w) //优先级比较函数
{
if (g->priority(w) > g->priority(v) + g->weight(v, w))
{
g->priority(w) = g->priority(v) + g->weight(v, w);
g->parent(w) = v;
}
};
PFS(s, DijkPU);
}复杂度同基于下标优先队列的prim算法,但前者不能保证得到最短路径,而后者求最短路径时不能解决带负权边的情况,如果已知最小负权值可以通过将所有权值加至正来解决。
prim算法每次添加的都是离生成树最近的,dilkstra每次添加的是离起点最近的
顺序查找的复杂度为O(n),其它几种查找算法为O(logn),暂不深究
若关键字为$k$,则其值存放在$f(k)$的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系$f$为散列函数,按这个思想建立的表为散列表 对不同的关键字可能得到同一散列地址,即$k_{1}\neq k_{2}$,而$f(k_{1})=f(k_{2})$,这种现象称为冲突(英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数$f(k)$和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。 若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
- n is the number of entries occupied in the hash table.
- k is the number of buckets.
查找成功的平均查找长度是针对元素的,查找不成功的平均查找长度是针对散列地址的.
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
好的散列函数具有的特征:确定,高效,满射(非严格意义,装填因子越大越好),均匀。 ** 直接定址法:取关键字或关键字的某个线性函数值为散列地址。即$hash(k)=k或hash(k)=a\cdot k+b,其中{\displaystyle a,b}a,b$为常数(这种散列函数叫做自身函数)
除留余数法:取关键字被某个不大于散列表表长m的数(可用位与运算取特定位)p除后所得的余数为散列地址。即
利用秦九韶算法可实现针对字符串的除留余数法,R如果比所有字符都大,就相当于将字符串看做一个R进制数,R只要足够小是结果不溢出即可,迭代算法中相对于普通的多项式计算多了对p取余的运算(每一步取余不易溢出),java用的基数是31,并且JVM会将“31 * i”优化成“(i<<5)- i”
除余法的缺陷:
-
不动点:H(0)=0;
-
零阶均匀:相邻关键码的散列地址也相邻
改进:MAD法
一阶均匀(不再满足零阶均匀),消除不动点。
考虑高阶还是低阶的均匀性视情况而定。
数字分析法:假设关键字是以r为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。 平方取中法:取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中的哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都相关(分解为一系列左移的和),由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。 折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。可以按自右向左的策略加,也可以按往复折返的策略加。对于二进制的key,可以用异或代替加。 (伪)随机数法:C库产生的随机数满足哈希表的要求(某一特定种子产生),但由于系统之间和编译器不同版本之间具体实现的差异使得可移植性差。$rand(x+1)=[a+rand(x)]\bmod M,a=7^5,M=INT_MAX\hash(key)=rand(key)=[rand(0)\times a^{key}]\bmod m$
每个桶本身再细分为若干槽位,用于存放彼此冲突的词条。每个桶槽位的词典结构为向量,因此整体物理存储结构类似于二维数组。 如:put操作,首先通过hash(key)定位到对应的桶单元,并在该桶内部槽位中进一步查找key,若没找到,则创建新词条插入到该桶的空闲槽位中。
缺点 绝大多数的槽位都处于空闲状态,造成空间浪费。若桶被细分为k个槽位,则装填因子将直接降低为原来的1/k. 很难实现确定应该细分为多少个槽位,才能保证够用。
将冲突的元素都放在对应位置的一条链表上。
装填因子是键数与链表数的比值即平均链表长度,大于1.
优点:
-
无需为每个桶预留槽位
-
任意次的冲突都可解决
-
删除操作实现简单
缺点
-
指针需要额外空间
-
节点需要动态申请
-
空间上不连续,不能利用系统缓存加速
一条链表的键数为k的概率在随机情况下(散列函数能将所有的键均匀的散布于各个链表中)满足二项分布,$\alpha$足够小时近似为泊松分布$\frac{\alpha^ke^{-\alpha}}{k!}$,查找长度对$\alpha$的偏离不会太大,条件很难满足,一般使用生成的伪随机数,但在不完全满足均匀的假设下也基本成立。
装填因子是键数与桶数的比值,小于1
为每个桶预先设立备用桶,构成一个查找链
查找时沿查找链逐个转向相邻的下一个桶单元,直到找到或遇到第一个空桶查找失败
缺点是以往的冲突会导致后面的冲突,并且不能装满,当$\alpha=1$时前面的冲突会导致无限循环。
懒惰删除(逻辑删除)
由于直接删除会切断查找链,所以删除时只标记,不实际删除,查找时越过,插入时看做空桶插入并修改标记
也是一个缺点,所以开放定制不适合
查找链中递增的gap变为平方,$[hash(key)+i^2]\bmod m$,各桶间间距线性递增,聚集线性缓解,前面的冲突对后面的影响大大降低;
缺点:
-
一旦涉及外存(容量较大),会破坏数据访问的局部性,缓存功能一定程度失效,I/O将激增,一般情况不会发生(对于一块1Kb的缓存,连续查找失败$\sqrt{1024/4}=16$次才会发生I/0交换,之后的探测需要其它地方存储的数据)
-
部分空桶不会被探测到,浪费空间
当M为素数时达到这个上界,且都集中在查找链的前端。
证明:反证法,假设存在$ 0<a<b<\lceil \frac{M}{2} \rceil$,使得沿着查找链,第a项与第b项彼此冲突,于是$a^2$与$b^2$同属M的某一同余类,即$a^2\equiv b^2;\bmod M \Rightarrow b^2-a^2=(b+a)(b-a)\equiv 0;\bmod M,然而,由假设知0<b-a<b+a<M$,b+a至少为2,是M的非平凡的因子,它与b-a之积不可能整除一个素数,假设不成立,故查找链的前半部分互异。
按$[hash(key)+i^2]\bmod m,[hash(key)-i^2]\bmod m$的方式双向试探
费马平方和定理
一个素数可以被分解为两个整数的平方之和,当且仅当它们是模4余1的。
由$(u^2+v^2)(s^2+t^2)=(us+vt)^2+(ut-vs)^2$可知一个整数可以表示为两个整数的平方和的形式,当且仅当它的素分解(质因数分解定理,$45=3*5^2$)中的模4余3类的素数的幂次为偶数(令$v^2=0,此项等于u^2$即可与其它平方和项合并),素数分解式迭代调用上式即可得到最终的分解式
当表长M为$4k+3$形式的素数,即素数的模4余3类时,双向平方试探的前M步不会发生冲突
证明:反证法,取M=4k+1,则查找链中的a,b两项满足$1\leq b<a\leq \lfloor\frac{M}{2}\rfloor$(初始是第0项),假设a,b的位置发生了冲突,则有$-b^2\equiv a^2;\bmod M\Rightarrow n=a^2+b^2\equiv 0;\bmod M$,则M是n的一个素因子,又M是模4余3的,所以它的平方(必然存在的一个偶幂次)也是n的因子,故$a^2+b^2\geq M$,这与条件是矛盾的,故假设不成立。
排序算法可以分为:
计算复杂度 就列表的大小而言的最佳、最差和平均情况下的行为。对于典型的串行排序算法,好的行为是 O( n log n ),并行排序是 O(log 2 n ),坏的行为是 O( n 2 )。串行排序的理想行为是 O( n ),但这在一般情况下是不可能的。最佳并行排序是 O(log n )。 交换/就地算法。 内存使用(以及其他计算机资源的使用)。特别是,一些排序算法是“就地”的。严格来说,就地排序只需要超出被排序项的 O(1) 内存;有时 O(log n )大小的额外内存被认为是“就地”。 递归:一些算法要么是递归的,要么是非递归的,而另一些算法可能两者兼而有之(例如,归并排序)。 稳定性:稳定的排序算法保持具有相等键(即值)的记录的相对顺序。 它们是否是比较排序。比较排序仅通过使用比较运算符比较两个元素来检查数据。 一般方法:插入、交换、选择、合并等。交换排序包括冒泡排序和快速排序。选择排序包括循环排序和堆排序。 算法是串行的还是并行的。本讨论的其余部分几乎完全集中于串行算法并假设串行操作。 适应性:输入的预排序是否影响运行时间。考虑到这一点的算法被认为是自适应的。 在线:在线的诸如插入排序之类的算法可以对恒定的输入流进行排序。 有序区增长/有序程度增长 内部/外部 静态/动态
桶排序(Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶里。每个桶再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序),最后依次把各个桶中的记录列出来记得到有序序列。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候,桶排序使用线性时间(Θ(n)),由于规模的差异,此时不受到O(n log n)下限的影响。 ** 桶排序是计数排序(每个桶内元素一样)的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,需要做到这两点:
在额外空间充足的情况下,尽量增大桶的数量 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
映射函数一般是 f = array[i] / k; k^2 = n; n是所有元素个数
或者 k=(highend-lowend)/interval;
平均时间复杂度:O(n + k) 最佳时间复杂度:O(n + k) 最差时间复杂度:取决于桶内所用的算法 空间复杂度:O(n * k) 稳定性:稳定
一个常见的优化是先将桶中未排序的元素放回原数组,然后对整个数组进行插入排序;因为插入排序的运行时间是基于每个元素离其最终位置的距离,所以比较的次数仍然相对较少,并且通过将列表连续存储在内存中可以更好地利用内存层次结构。
如果输入分布已知或可以估计,通常可以选择包含恒定密度(而不仅仅是具有恒定大小)的桶。这允许在即使没有均匀分布的输入的情况下得到较低时间和空间复杂度。
两个桶的桶排序实际上是快速排序的一个版本,其中枢轴值总是被选择为值范围的中间值。虽然这种选择对均匀分布的输入有效,但在快速排序中选择枢轴的其他方法(例如随机选择的枢轴)使其更能抵抗输入分布中的聚类。
基数排序可以实现为从最高有效数字(MSD) 或最低有效数字(LSD) 开始。例如,对于1234,可以从1(MSD)或4(LSD)开始。
LSD 基数排序通常使用以下排序顺序:短键先于长键,然后按字典顺序对相同长度的键进行排序。这与整数表示的正常顺序一致,如序列[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]。LSD分类通常是稳定的排序。
MSD 基数排序最适合于对字符串或固定长度的整数表示形式进行排序。像[b, c, e, d, f, g, ba]这样的序列将排序为[b, ba, c, d, e, f, g]。如果使用词典排序对以 10 为基数的可变长度整数进行排序,则从 1 到 10 的数字将输出为[1, 10, 2, 3, 4, 5, 6, 7, 8, 9],就好像较短的键是左对齐的,并在右侧填充空白字符,以使较短的键与最长的键一样长。如果必须始终保持重复密钥的原始顺序,则 MSD 排序不一定稳定。
除了遍历顺序之外,MSD 和 LSD 排序在处理可变长度输入方面也有所不同。LSD 排序可以按长度分组,基数对每个组进行排序,然后按大小顺序连接组。MSD 排序必须有效地将所有较短的键"扩展"到最大键的大小,并相应地对它们进行排序,这可能比 LSD 所需的分组更复杂。
但是,MSD 排序更适合细分和递归。由 MSD 步骤创建的每个存储桶本身都可以使用下一个最高有效数字进行基数排序,而无需引用在上一步中创建的任何其他存储桶。到达最后一位数字后,只需连接存储桶即可完成排序。
//MSD core
for(int i = 0; i < n; i++){
if(num[i] == 1){ //如果桶中只有一个数则直接取出
A[c++] = t[i][0];
}else if(num[i] > 1){ //如果桶中不止一个数,则另存如数组B递归
int[] B = new int[num[i]];
for(int j = 0;j < num[i];j++){
B[j] = t[i][j];
sort(B,num[i]); //递归
}
}
}MSD:分,分,分,连;LSD:分,连,分,连
设待排序的数组R[1..n],数组中最大的数是d位数,基数为r(如基数为10,即10进制,最大有10种可能,即最多需要10个桶来映射数组元素)。
LSD:处理一位数,需要将数组元素映射到r个桶中,映射完成后还需要收集,相当于遍历数组一遍,最多元素数为n,则时间复杂度为O(n+r)。所以,总的时间复杂度为O(d*(n+r))=O(dn).空间复杂度为O(d+n),d为桶数,MSD空间复杂度略大,时间复杂度略小,两者渐进意义下是一致的
以待排序序列建立大根堆,不断的取出堆顶元素并与数组中非有序区的末元素(有序区的-1位置)交换位置,并进行下滤调整,最终得到升序序列
template <typename T, typename Comp = std::less<T>> //默认升序
void heapSort(std::vector<T> &array, Comp comp = std::less<T>())
{
//由于malloc不调用构造函数所以在有内存监测的情况下不能使用string,否则赋值时会报错
PQueen<T, T> Q(array); //默认建立小根堆,产生降序序列
for (int i = Q.n - 1; i > 0; i--)
{
std::swap(Q.elem[i], Q.elem[0]);
Q.siftDown(0, i); //注意siftDown是前闭后开的
}
for (int i = 0; i < Q.n; i++) //根据比较函数类型重新填入结果
if (std::is_same<decltype(comp), std::less<T>>::value) //降序
array[Q.n - i - 1] = Q.elem[i]->key;
else //升序
array[i] = Q.elem[i]->key;
}template <typename T, typename Comp>
void merge(vector<T> &array, int lo, int mi, int hi, Comp comp)
{
int i = 0, j = 0, lb = mi - lo;
//由于使用vector,A和C不能显式表示,array[lo+i]=A[i],array[mi+i]=C[i];
vector<T> B(array.begin() + lo, array.begin() + mi); //前子向量B[0, lb) <-- A[lo, mi),拷贝
int k = 0, lc = hi - mi;
//后子向量C[0, lc) = A[mi, hi),就地
while ((j < lb) && (k < lc)) //反复地比较B、C的首元素
array[lo + i++] = !comp(array[mi + k], B[j]) ? B[j++] : array[mi + k++]; //将更小(大)者归入A中
while (j < lb) //若C先耗尽,则
array[lo + i++] = B[j++]; //将B残余的后缀归入A中,若B先耗尽,由于C在原空间存储,故可以退出循环(注意,C对应的指针位始终在A之前,不可能发生覆盖)
}
template <typename T, typename Comp> //向量归并排序
void _mergeSort(vector<T> &array, int lo, int hi, Comp comp)
{
if (hi - lo < 2)
return; //单元素区间自然有序,否则...
int mi = (lo + hi) / 2; //以中点为界
_mergeSort(array, lo, mi, comp);//区间前闭后开
_mergeSort(array, mi, hi, comp); //分别排序
merge(array, lo, mi, hi, comp); //合并
}
template <typename T, typename Comp = std::less<T>>//需要提供默认模板参数类型,否则缺省状态不能推断出
void mergeSort(vector<T> &array, Comp comp = std::less<T>()) //注意作为默认形参要带括号(是一个实例),作为参数类型则不带
{
_mergeSort(array, 0, array.size(), comp);
}所示为递归法
递归法(Top-down)(二路归并) 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列 设定两个指针,最初位置分别为两个已经排序序列的起始位置 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置 重复步骤3直到某一指针到达序列尾 将另一序列剩下的所有元素直接复制到合并序列尾
迭代法(Bottom-up)(一趟归并) 原理如下(假设序列共有n个元素): 将序列每相邻两个数字进行归并操作,形成 ceil(n/2)个序列,排序后每个序列包含两/一个元素 若此时序列数不是1个则将上述序列再次归并,形成ceil(n/4)个序列,每个序列包含四/三个元素 重复步骤2,直到所有元素排序完毕,即序列数为1
时间复杂度O(nlogn),空间O(n)(递归法需要O(logn)的递归栈空间,迭代法不需要)
与mergeSort类似都是递归的,区别在于mergeSort的难点在于合并,而quickSort的难点在于划分
快速排序是逐个将每个元素转换为轴点的过程
选边界元素做轴点时从另一端开始扫描
The steps for in-place quicksort are:
- If the range has less than two elements, return immediately as there is nothing to do. Possibly for other very short lengths a special-purpose sorting method is applied and the remainder of these steps skipped.
- Otherwise pick a value, called a pivot, that occurs in the range (the precise manner of choosing depends on the partition routine, and can involve randomness).
- Partition the range: reorder its elements, while determining a point of division, so that all elements with values less than the pivot come before the division, while all elements with values greater than the pivot come after it; elements that are equal to the pivot can go either way. Since at least one instance of the pivot is present, most partition routines ensure that the value that ends up at the point of division is equal to the pivot, and is now in its final position (but termination of quicksort does not depend on this, as long as sub-ranges strictly smaller than the original are produced).
- Recursively apply the quicksort to the sub-range up to the point of division and to the sub-range after it, possibly excluding from both ranges the element equal to the pivot at the point of division. (If the partition produces a possibly larger sub-range near the boundary where all elements are known to be equal to the pivot, these can be excluded as well.)
复杂度:T(n)=T(k)+T(n-k-1)+O(n),轴点的选择至关重要
主要是递归造成的栈空间的使用,最好情况,递归树的深度为 log2n
空间复杂度也就为 O(logn)
最坏情况,
需要进行n‐1递归调用,其空间复杂度为O(n),
均匀独立分布时
递归求解得到C ( n ) = 2 n ln n ≈ 1.39 n log 2 n
所以算法平均情况下的复杂度为O(nlogn),最坏情况为O(n^2/2)=O(n);
时间复杂度:
- O(nlogn):堆排序,快速排序(平均),归并排序
- O(n)到O(n^2):希尔排序
- 其余O(n^2),折半插入比普通插入平均意义上更快,但渐进意义上是一致的
- 简单插入排序的复杂度与数据的分布无关,上下限一致
- 从最好情况看(顺序):直接插入排序和起泡排序最好,为O(n),其余与平均相同
- 从最坏情况看(逆序):快速排序为O(n^2),直接插入与起泡系数增加大约一倍,最坏情况对简单选择排序,堆排序和归并排序影响不大、
- 在最好情况下,直接插入和起泡排序最快,在平均情况下,快速排序最快,最坏情况下,堆排序和归并排序最快
空间复杂度:
- O(n):归并排序,基数排序
- 0(logn)到O(n),快速排序
- 其余为O(1)
稳定性
- 不稳定的:直接选择排序,希尔排序,快速排序和堆排序
- 其余稳定