09.Array-Bucket-Sort.md

1. 桶排序算法思想

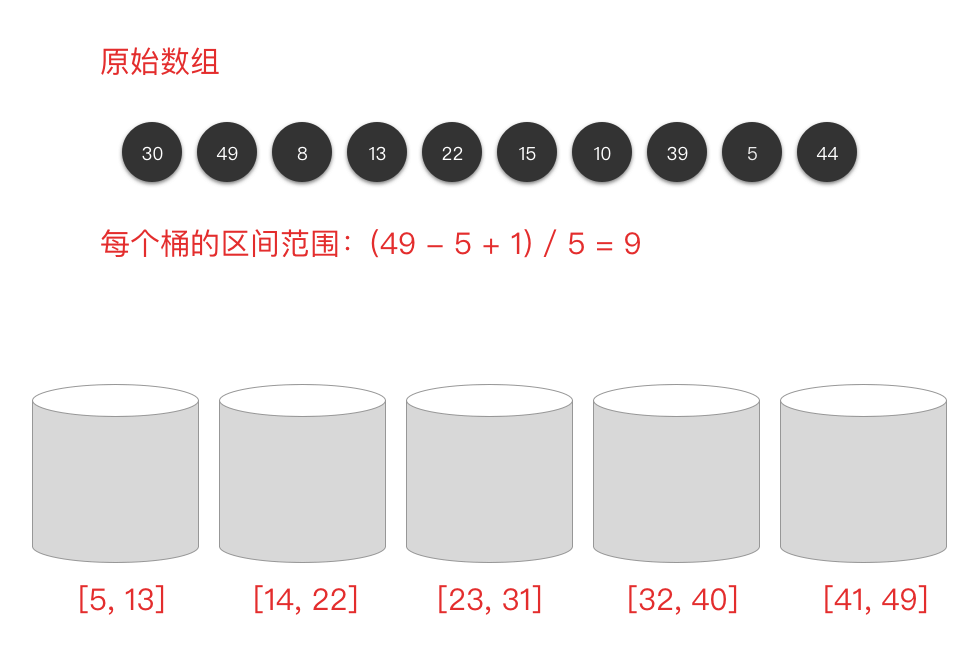
桶排序（Bucket Sort）基本思想：

将未排序的数组分到若干个「桶」中，每个桶的元素再进行单独排序。

2. 桶排序算法步骤

• 将区间划分为 n 个相同大小的子区间，每个区间称为一个桶。
• 遍历数组，将每个元素装入对应的桶中。
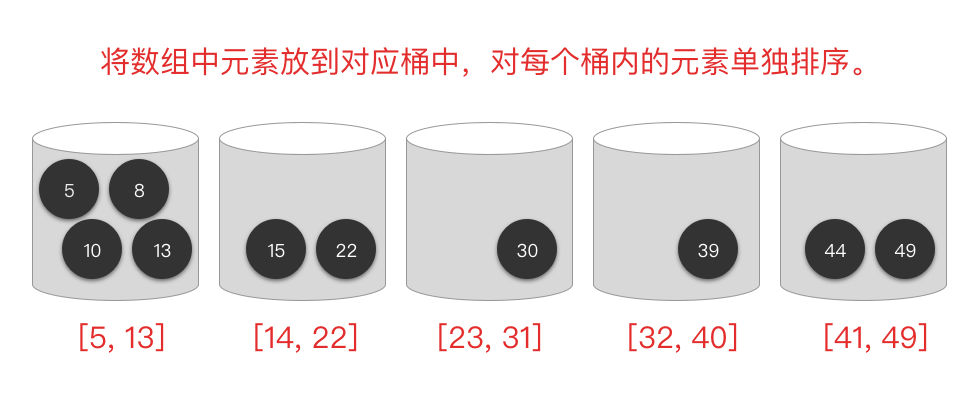
• 对每个桶内的元素单独排序（使用插入、归并、快排等算法）。
• 最后按照顺序将桶内的元素合并起来。

3. 桶排序图解演示

3.1 划分子区间

3.2 将数组元素装入桶中，并对桶内元素单独排序

3.3 将桶内元素合并起来，完成排序

4. 桶排序算法分析

• 桶排序可以在线性时间内完成排序，当输入元素个数为 n，桶的个数是 m 时，每个桶里的数据就是 k = n / m 个。每个桶内排序的时间复杂度为 $O(k * log_2k)$。m 个桶就是 $m * O(k * log_2k) = m * O((n/m)log_2(n/m)) = O(nlog_2(n/m))$。当桶的个数 m 接近于数据个数 n 时，$log_2(n/m)$ 就是一个较小的常数，所以排序桶排序时间复杂度接近于 $O(n)$。
• 由于桶排序使用了辅助空间，所以桶排序的空间复杂度是 $o(n + m)$。
• 如果桶内使用插入排序算法等稳定排序算法，则桶排序也是 稳定排序算法。

5. 桶排序代码实现

class Solution:
    def insertionSort(self, arr):
        for i in range(1, len(arr)):
            temp = arr[i]
            j = i
            while j > 0 and arr[j - 1] > temp:
                arr[j] = arr[j - 1]
                j -= 1
            arr[j] = temp

        return arr

    def bucketSort(self, arr, bucket_size=5):
        arr_min, arr_max = min(arr), max(arr)
        bucket_count = (arr_max - arr_min) // bucket_size + 1
        buckets = [[] for _ in range(bucket_count)]

        for num in arr:
            buckets[(num - arr_min) // bucket_size].append(num)

        res = []
        for bucket in buckets:
            self.insertionSort(bucket)
            res.extend(bucket)

        return res

    def sortArray(self, nums: List[int]) -> List[int]:
        return self.bucketSort(nums)