Skip to content

Latest commit

 

History

History
317 lines (196 loc) · 8.37 KB

PA1_template.md

File metadata and controls

317 lines (196 loc) · 8.37 KB
Raw

Reproducible Research: Peer Assessment 1

Exam time again!!!

Here's a useful link to help Rmarkdown writing, by Rstudio : R Markdown cheat sheet

Loading libraries

library(lubridate,warn.conflicts = F)
library(dplyr,warn.conflicts = F)
library(ggplot2)

#To make AWESOME tables
library(xtable)

Loading and preprocessing the data

if (!file.exists("activity.csv")) unzip("activity.zip")

d <- read.csv("activity.csv", stringsAsFactors = F)

# data<-data[complete.cases(data),]

data <- mutate(d, date = ymd(date))

What is mean total number of steps taken per day?

Aggregating datas

# dplyr version sumSteps<-d %>% group_by(date) %>% summarise( sum(steps))

# Basic version
sumSteps <- aggregate(steps ~ date, data = d, FUN = sum)

# renaming columns for convenience
colnames(sumSteps) = c("Date", "Steps")

# Computing median and mean

Mean1 <- as.integer(round(mean(sumSteps$Steps, na.rm = T), 0))
Median1 <- as.integer(round(median(sumSteps$Steps, na.rm = T), 0))

Now plotting time

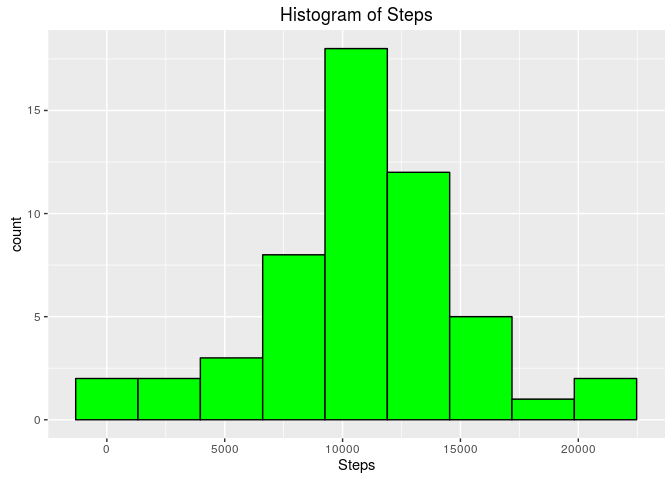
ggplot(sumSteps, aes(Steps)) + geom_histogram(bins = 9, col = "black", fill = "green") + 
    ggtitle("Histogram of Steps")

The mean total number of steps taken per day is 10766 and the median is 10765

The choice of 9 beans instead the default of 30 bins by ggplot has been made to have kind of a 'Gaussian' look, with no empty bean.

From this graphic, we can note

  • Data looks like normally distributed
  • Th mean and the median being very close, reinforcing this impression

Let's go play and superpose a bell-shaped curve to the graph

We'll draw the corresponding Gaussian distribution:

  • Mean= 1.0766189\times 10^{4}
  • Standard deviation = 4269.1804927
ggplot(sumSteps, aes(Steps))+
  geom_histogram( aes(y=..density..), bins=9,col='black', fill='green')+
  stat_function(fun=dnorm, colour='red', lwd=2, args=list(mean=mean(sumSteps$Steps), sd=sd(sumSteps$Steps)))+
  ggtitle('Comparing histogram and normal distribution')

The graphic belows shows:

  • Histogram : in green
  • Density plot: in blue
  • Gaussian distribution : in red
ggplot(sumSteps, aes(Steps))+
  geom_histogram( aes(y=..density..), bins=30,col='black', fill='green')+
  geom_density(colour='blue', lwd=1, fill='blue', alpha=0.3)+
  stat_function(fun=dnorm, colour='red', lwd=2, args=list(mean=mean(sumSteps$Steps), sd=sd(sumSteps$Steps)))+
  ggtitle('Comparing histogram and normal distribution with 30 bins histograms')

Comparison not so obvious.... for the histogram, as it depends on number of bins

However, we get a better feel with the density plotting (in blue)

What is the average daily activity pattern?

First, we do aggregate data by interval

I enclosed 2 versions of the aggregation code:

  • One using the dplyr package, as My personal goal is to mater it, as it is more flexible and advanced than the 'base' package
  • Another one using Ocam's razor aggregate() function
# dplyr version daily<-d %>% group_by(interval) %>%
# summarise(steps=mean(steps, na.rm=T))
daily <- aggregate(steps ~ interval, data = d, FUN = function(x) {
    mean(x, na.rm = T)
})

Now about the plotting, the assigment required a line plot, that you can find below. However, this plot does'nt show the missing intervals, so I built a 'barplot', with the line plot ovrlay clearly showing the data 'holes'

Line plot of activity pattern

ggplot(daily, aes(x=interval,y=steps) ) + 
  geom_line(col='red')

Barplot with Line plot overlay

This one shows clearly how ggplot operates

  • barplot in blue
  • lineplot in red

Both using the same dataset

ggplot(daily, aes(x=interval,y=steps) ) + 
  geom_bar(stat = 'identity',col='blue')+ 
  geom_line(col='red')

The interval having the maximal mean step value being

**

daily[[which.max(daily$steps),1]]
## [1] 835

**

Imputing missing values

Let's count missing values

t<-table(is.na(d), dnn = 'Missing Values')

#now making it look AWESOME with xtable
print(xtable(t), type = 'html')
Missing Values
FALSE 50400
TRUE 2304

So there are 2304 missing values out of 52704 (about 4.37%)

Now filling missing values

The filling strategy is as following: We'll replace the missing intervals for a specific day with the average of this interval

#First: Build a table of means by interval
meanByIntervalAndDate <- d %>%group_by(interval,date) %>% summarize(steps=mean(steps, rm.na=T))
meanByInterval  <-aggregate(steps~interval, data=meanByIntervalAndDate, FUN=function(x) {mean(x,na.rm=TRUE)})

# Then we split data in two parts: the NA part and the non-NA part
naIndexes <-is.na(d$steps)

# We keep the NA lines and drop the 'steps' (containig only NAs) column
naPart= d[naIndexes,]
naPart$steps=NULL

#We drop the NA lines from the data
nonNaPart=d[!naIndexes,]

#Then we do a left join with the 'Mean by interval' table 
naPart<-left_join(naPart, meanByInterval, by='interval')

# We check that all lines have been filled
length(naPart[is.na(naPart$steps),'steps'])
## [1] 0

#Then we go for row_bind betwen the naPartand the nonNaPart

d <- bind_rows(naPart, nonNaPart)

Now that we have a new dataframe,it is time to bilsdan histogram to check if the fact of filling data had an impact

sumSteps2 <- aggregate(steps ~ date, data = d, FUN = sum)

# renaming columns for convenience
colnames(sumSteps2) = c("Date", "Steps")

# computing median and mean
Mean2 <- as.integer(round(mean(sumSteps2$Steps, na.rm = T), 0))
Median2 <- as.integer(round(median(sumSteps2$Steps, na.rm = T), 0))


ggplot(sumSteps2, aes(Steps)) + geom_histogram(bins = 9, col = "black", fill = "green") + 
    ggtitle("Histogram of Steps")

** For this new dataset **

The mean total number of steps taken per day is 10766 and the median is 10766

So we notice that the mean didn't change after having filled data. However, the median increased by 1 unit (10765 to 10766), a 0.01% change what is non significative

Are there differences in activity patterns between weekdays and weekends?

This part is two fold: 1 Create a new factor variable in the dataset with two levels – “weekday” and “weekend” indicating whether a given date is a weekday or weekend day.

2 Make a panel plot containing a time series plot (i.e. type = "l") of the 5-minute interval (x-axis) and the average number of steps taken, averaged across all weekday days or weekend days (y-axis). See the README file in the GitHub repository to see an example of what this plot should look like using simulated data.

Step one: adding the 'daytype' factor to the dataset

# adding the weekday factor

#To do so, we use the wday() function what return 1 for sunday, 7for saturday, and 2..6 for the other weekday
d<-mutate(d,dayType= ifelse(wday(date) %in% c(1,7), 'weekend', 'weekday'))

#Makes it a factor, as requested
d$dayType<-as.factor(d$dayType)

Step two: Creating the plot

dailyByDayType <- aggregate(steps ~ interval + dayType, data = d, FUN = function(x) {
    mean(x, na.rm = T)
})

ggplot(dailyByDayType, aes(interval, steps)) + geom_area(col = "red", fill = "red") + 
    facet_grid(dayType ~ .)

So we can see there is a difference in activity level between the weekdays and the weekends!

##Bonus track

A variant of the plot, what shows better the difference in the activity levels

dailyByDayType <- aggregate(steps ~ interval + dayType, data = d, FUN = function(x) {
    mean(x, na.rm = T)
})

ggplot(dailyByDayType, aes(interval, steps, coloour = dayType, fill = dayType)) + 
    geom_area(col = "black", alpha = 0.5)