time-complexity.md

title	description	hide_table_of_contents	keywords
Time Complexity	Time Complexity is one of the important measurements when it comes to writing an efficient solution.	true	leetcode tutorial time complexity

Overview

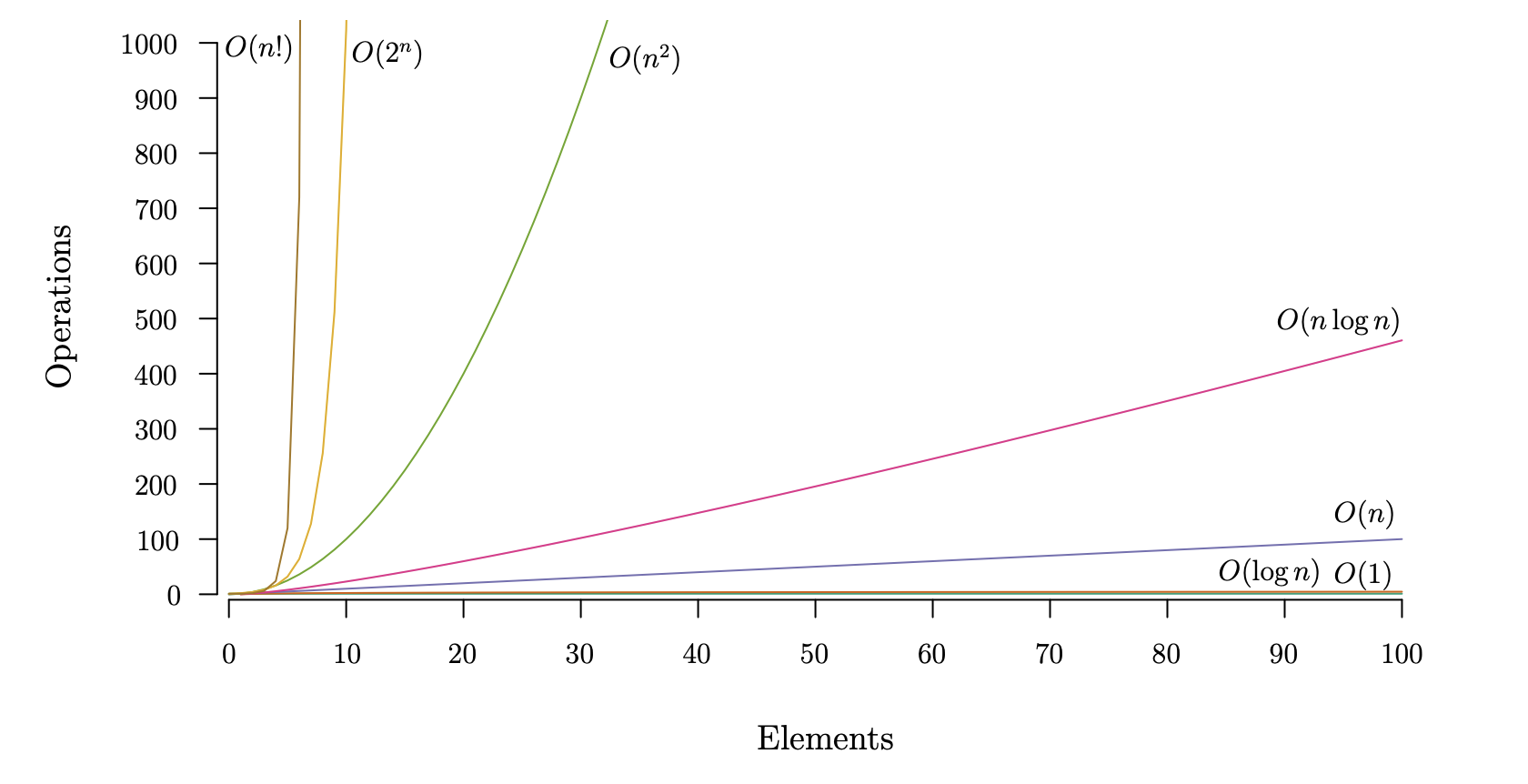
Time Complexity is one of the important measurements when it comes to writing an efficient solution. It estimates how much time your solution needs based on some input. If your solution is too slow, even it passes some test cases, it will still consider it as a wrong answer.

The time complexity is denoted by Big O notation. Normally, $$n$$ means the input size. For example, if the input is a string $$s$$, then $$n$$ would be the length of $$s$$.

Estimating Time Complexity

Input size	Time Complexity
$$n <= 10$$	$$O(n!), O(n^7),O(n^6)$$
$$n <= 20$$	$$O(2^n)$$
$$n <= 80$$	$$O(n^4)$$
$$n <= 400$$	$$O(n^3)$$
$$n <= 7500$$	$$O(n^2)$$
$$n <= 10^6$$	$$O(nlogn)$$, $$O(n)$$
$$large$$	$$O(1)$$, $$O(logn)$$

Example 1:

In the following case, the time complexity depends on $$n$$. Therefore, it is $$O(n)$$.

for (int i = 0; i < n; i++) {
  // do something
}

Example 2:

In the following case, the time complexity depends on $$n$$ and $$m$$. Therefore, it is $$O(n*m)$$.

for (int i = 0; i < n; i++) {
  for (int j = 0; j < m; j++) {
    // do something
  }
}

Example 3:

In the following case, the time complexity is $$O(\sqrt n)$$. You can see $$i * i <= n$$ as $$i <= \sqrt n$$.

As sqrt() returns double, it would be safe to use $i * i <= n$ to check the condition instead of using $i <= sqrt(n)$.

for (int i = 2; i * i <= n; i++) {
  // do something
}

Useful Resources

• Big-O_Cheat_Sheet-Letter.pdf
• BIG-O.pdf