贡献者:姚鑫、艾春辉,芙蕖,李玲
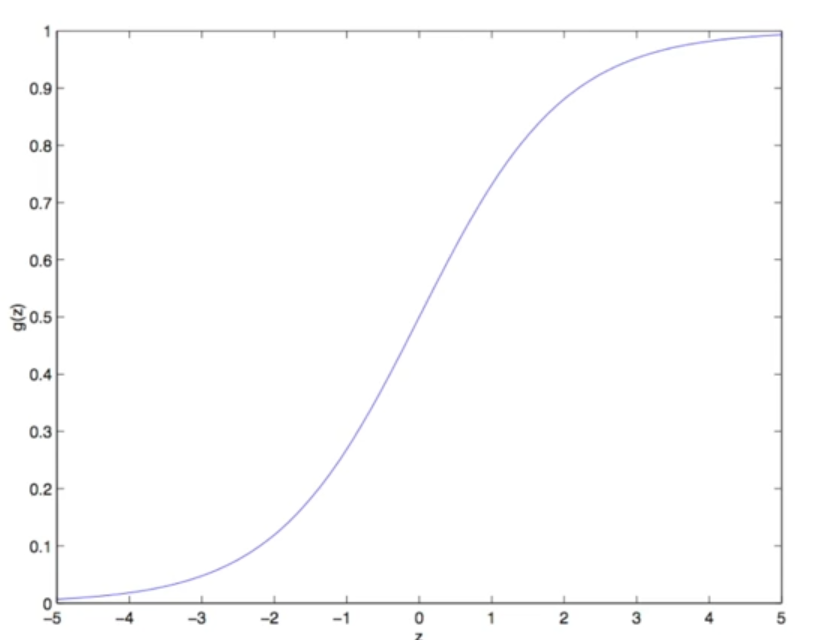
LR是Logistic Regression Classifier,本质上是线性回归,特殊之处在于特征到结果的映射中加入了一层逻辑函数g(z),即先把特征线性求和,然后使用函数g(z)作为假设函数来预测。g(z)可以将连续值映射到0 和1。逻辑回归使用的g(z)函数是sigmoid函数。因此逻辑回归=线性回归 + sigmoid。
逻辑回归的表达式为
图像
逻辑回归的优点:
- 它是直接对分类可能性进行建模,无需实现假设数据分布,这样就避免了假设分布不准确所带来的问题;
- 它不是仅预测出“类别”,而是可得到近似概率预测,这对许多需利用概率辅助决策的任务很有用;
- 逻辑回归函数是任意阶可导的凸函数,有很好的数学性质,现有的许多数值优化算法都可直接用于求取最优解。
- 对于线性数据,(大部分时候)逻辑回归的拟合和计算都非常快,计算效率优于SVM和随机森林
假设数据集为 $$ Data: {{(x_i, y_i)}}^{N}_{i=1} \ x_i\in \mathbb{R}^p,y_i\in{0,1} $$ sigmoid函数为 $$ sigmoid:\sigma(z)=\frac{1}{1+e^{-z}} $$ 在线性回归中有 $$ y=w^Tx+b $$ 为了方便,我们将其中的权值向量$w$和输入向量$x$进行扩充,即$w=(w_1,w_2,...,w_n,b)$;$x=(x_1,x_2,...,x_n,1)$,则式(3)可以改写为$y=w^Tx$
线性回归是将向量$x$映射为具体的数值$y$(连续),而逻辑回归是用来解决分类问题(通常为二分类问题),希望得到$0$或$1$的概率(区间$[0,1]$),即通过某种方式将数值$y$映射到区间$[0,1]$范围内。逻辑回归采用sigmoid函数来完成这样的映射,从而建立$y$与$x$之间的概率判别模型 $$ P(Y|X) $$ 有 $$ p_1=P(y=1|x)=\frac{1}{1+e^{-(w^Tx)}} $$
得到 $$ P(Y|X)=p_1^Yp_0^{1-Y},Y\in{0,1} $$ 对应的似然函数为 $$ \prod_{i=1}^NP(y_i|x_i) $$ 取对数,得到对数似然函数 $$ \begin{align} L(w)&=\sum_{i=1}^{N}\log P(y_i|x_i) \ &=\sum_{i=1}^{N}(y_i\log p_1 + (1-y_i)\log p_0) \ &=\sum_{i=1}^{N}(y_i\log p_1 + (1-y_i)\log (1-p_1)) \ &=\sum_{i=1}^{N}(y_i(\log p_1-\log (1-p_1)) + \log(1-p_1)) \ &=\sum_{i=1}^{N}(y_i\log(\frac{p_1}{1-p_1}) + \log(1-p_1)) \ &=\sum_{i=1}^{N}(y_i(w^Tx_i)+\log{\frac{e^{-(w^Tx_i)}}{1+e^{-(w^Tx_i)}}}) \ &=\sum_{i=1}^{N}(y_i(w^Tx_i)+\log{\frac{1}{1+e^{w^Tx_i}}}) \ &=\sum_{i=1}^{N}(y_i(w^Tx_i)-\log{(1+e^{w^Tx_i})}) \end{align} $$ 对$L(w)$求极大值(即极大似然估计),即可得到$w$的估计值 $$ \hat w=\mathop{\arg\max}_{w}L(w) $$
这样,问题就变成了以对数似然函数为目标的最优化问题,可采用梯度下降法或拟牛顿法。
令$g(w^Tx_i)=\frac{1}{1+e^{-(w^Tx_i)}}$
因为这里是求最大值,采用梯度上升法: