There is a long and thin painting that can be represented by a number line. You are given a 0-indexed 2D integer array paint of length n, where paint[i] = [starti, endi]. This means that on the ith day you need to paint the area between starti and endi.
Painting the same area multiple times will create an uneven painting so you only want to paint each area of the painting at most once.
Return an integer array worklog of length n, where worklog[i] is the amount of new area that you painted on the ith day.
Example 1:
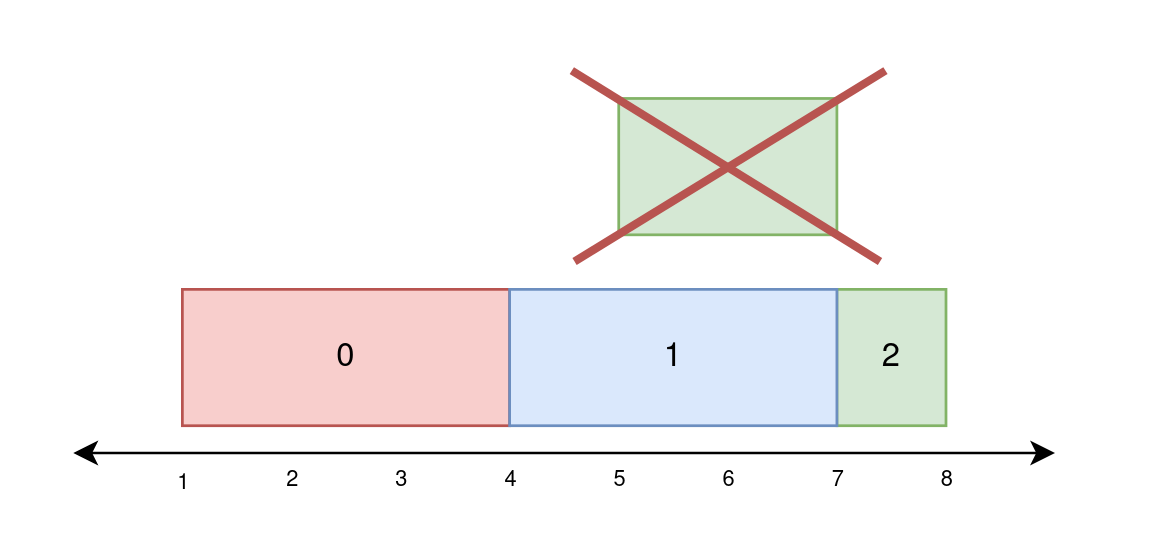
Input: paint = [[1,4],[4,7],[5,8]] Output: [3,3,1] Explanation: On day 0, paint everything between 1 and 4. The amount of new area painted on day 0 is 4 - 1 = 3. On day 1, paint everything between 4 and 7. The amount of new area painted on day 1 is 7 - 4 = 3. On day 2, paint everything between 7 and 8. Everything between 5 and 7 was already painted on day 1. The amount of new area painted on day 2 is 8 - 7 = 1.
Example 2:
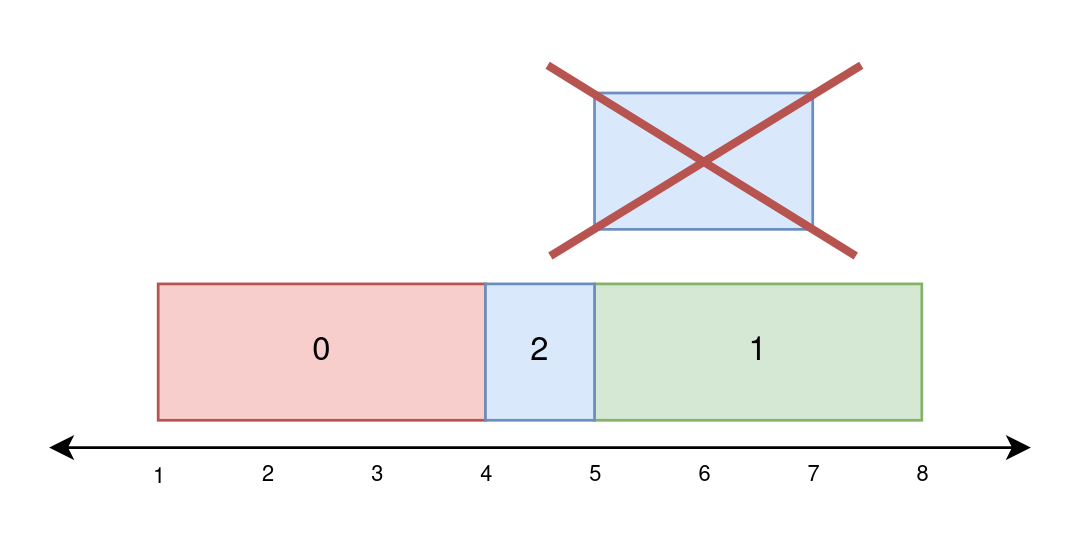
Input: paint = [[1,4],[5,8],[4,7]] Output: [3,3,1] Explanation: On day 0, paint everything between 1 and 4. The amount of new area painted on day 0 is 4 - 1 = 3. On day 1, paint everything between 5 and 8. The amount of new area painted on day 1 is 8 - 5 = 3. On day 2, paint everything between 4 and 5. Everything between 5 and 7 was already painted on day 1. The amount of new area painted on day 2 is 5 - 4 = 1.
Example 3:
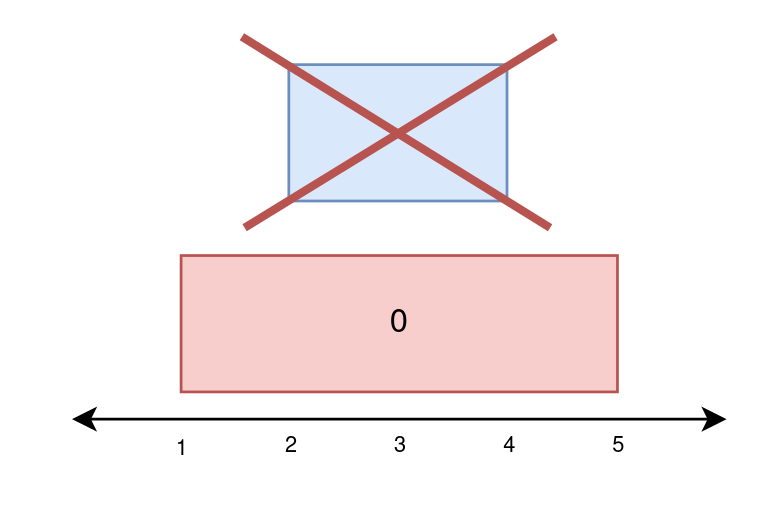
Input: paint = [[1,5],[2,4]] Output: [4,0] Explanation: On day 0, paint everything between 1 and 5. The amount of new area painted on day 0 is 5 - 1 = 4. On day 1, paint nothing because everything between 2 and 4 was already painted on day 0. The amount of new area painted on day 1 is 0.
Constraints:
1 <= paint.length <= 105paint[i].length == 20 <= starti < endi <= 5 * 104
方法一:线段树
线段树将整个区间分割为多个不连续的子区间,子区间的数量不超过 log(width)。更新某个元素的值,只需要更新 log(width) 个区间,并且这些区间都包含在一个包含该元素的大区间内。区间修改时,需要使用懒标记保证效率。
- 线段树的每个节点代表一个区间;
- 线段树具有唯一的根节点,代表的区间是整个统计范围,如
[1, N]; - 线段树的每个叶子节点代表一个长度为 1 的元区间
[x, x]; - 对于每个内部节点
[l, r],它的左儿子是[l, mid],右儿子是[mid + 1, r], 其中mid = ⌊(l + r) / 2⌋(即向下取整)。
对于本题,线段树节点维护的信息有:
- 区间中元素大于 0 的个数 v
- 懒标记 add
class Node:
def __init__(self, l, r):
self.left = None
self.right = None
self.l = l
self.r = r
self.mid = (l + r) >> 1
self.v = 0
self.add = 0
class SegmentTree:
def __init__(self):
self.root = Node(1, 10**5 + 10)
def modify(self, l, r, v, node=None):
if l > r:
return
if node is None:
node = self.root
if node.l >= l and node.r <= r:
node.v = node.r - node.l + 1
node.add = v
return
self.pushdown(node)
if l <= node.mid:
self.modify(l, r, v, node.left)
if r > node.mid:
self.modify(l, r, v, node.right)
self.pushup(node)
def query(self, l, r, node=None):
if l > r:
return 0
if node is None:
node = self.root
if node.l >= l and node.r <= r:
return node.v
self.pushdown(node)
v = 0
if l <= node.mid:
v += self.query(l, r, node.left)
if r > node.mid:
v += self.query(l, r, node.right)
return v
def pushup(self, node):
node.v = node.left.v + node.right.v
def pushdown(self, node):
if node.left is None:
node.left = Node(node.l, node.mid)
if node.right is None:
node.right = Node(node.mid + 1, node.r)
if node.add:
left, right = node.left, node.right
left.v = left.r - left.l + 1
right.v = right.r - right.l + 1
left.add = node.add
right.add = node.add
node.add = 0
class Solution:
def amountPainted(self, paint: List[List[int]]) -> List[int]:
tree = SegmentTree()
ans = []
for i, (start, end) in enumerate(paint):
l, r = start + 1, end
v = tree.query(l, r)
ans.append(r - l + 1 - v)
tree.modify(l, r, 1)
return ansclass Node {
Node left;
Node right;
int l;
int r;
int mid;
int v;
int add;
public Node(int l, int r) {
this.l = l;
this.r = r;
this.mid = (l + r) >> 1;
}
}
class SegmentTree {
private Node root = new Node(1, 100010);
public SegmentTree() {
}
public void modify(int l, int r, int v) {
modify(l, r, v, root);
}
public void modify(int l, int r, int v, Node node) {
if (l > r) {
return;
}
if (node.l >= l && node.r <= r) {
node.v = node.r - node.l + 1;
node.add = v;
return;
}
pushdown(node);
if (l <= node.mid) {
modify(l, r, v, node.left);
}
if (r > node.mid) {
modify(l, r, v, node.right);
}
pushup(node);
}
public int query(int l, int r) {
return query(l, r, root);
}
public int query(int l, int r, Node node) {
if (l > r) {
return 0;
}
if (node.l >= l && node.r <= r) {
return node.v;
}
pushdown(node);
int v = 0;
if (l <= node.mid) {
v += query(l, r, node.left);
}
if (r > node.mid) {
v += query(l, r, node.right);
}
return v;
}
public void pushup(Node node) {
node.v = node.left.v + node.right.v;
}
public void pushdown(Node node) {
if (node.left == null) {
node.left = new Node(node.l, node.mid);
}
if (node.right == null) {
node.right = new Node(node.mid + 1, node.r);
}
if (node.add != 0) {
Node left = node.left, right = node.right;
left.add = node.add;
right.add = node.add;
left.v = left.r - left.l + 1;
right.v = right.r - right.l + 1;
node.add = 0;
}
}
}
class Solution {
public int[] amountPainted(int[][] paint) {
SegmentTree tree = new SegmentTree();
int n = paint.length;
int[] ans = new int[n];
for (int i = 0; i < n; ++i) {
int l = paint[i][0] + 1;
int r = paint[i][1];
int v = tree.query(l, r);
ans[i] = r - l + 1 - v;
tree.modify(l, r, 1);
}
return ans;
}
}class Node {
public:
Node* left;
Node* right;
int l;
int r;
int mid;
int v;
int add;
Node(int l, int r) {
this->l = l;
this->r = r;
this->mid = (l + r) >> 1;
this->left = this->right = nullptr;
v = add = 0;
}
};
class SegmentTree {
private:
Node* root;
public:
SegmentTree() {
root = new Node(1, 100010);
}
void modify(int l, int r, int v) {
modify(l, r, v, root);
}
void modify(int l, int r,int v, Node* node) {
if (l > r) return;
if (node->l >= l && node->r <= r)
{
node->v = node->r - node->l + 1;
node->add = v;
return;
}
pushdown(node);
if (l <= node->mid) modify(l, r, v, node->left);
if (r > node->mid) modify(l, r, v, node->right);
pushup(node);
}
int query(int l, int r) {
return query(l, r, root);
}
int query(int l, int r, Node* node) {
if (l > r) return 0;
if (node->l >= l && node-> r <= r) return node->v;
pushdown(node);
int v = 0;
if (l <= node->mid) v += query(l, r, node->left);
if (r > node->mid) v += query(l, r, node->right);
return v;
}
void pushup(Node* node) {
node->v = node->left->v + node->right->v;
}
void pushdown(Node* node) {
if (!node->left) node->left = new Node(node->l, node->mid);
if (!node->right) node->right = new Node(node->mid + 1, node->r);
if (node->add)
{
Node* left = node->left;
Node* right = node->right;
left->v = left->r - left->l + 1;
right->v = right->r - right->l + 1;
left->add = node->add;
right->add = node->add;
node->add = 0;
}
}
};
class Solution {
public:
vector<int> amountPainted(vector<vector<int>>& paint) {
int n = paint.size();
vector<int> ans(n);
SegmentTree* tree = new SegmentTree();
for (int i = 0; i < n; ++i)
{
int l = paint[i][0] + 1;
int r = paint[i][1];
int v = tree->query(l, r);
ans[i] = r - l + 1 - v;
tree->modify(l, r, 1);
}
return ans;
}
};