README.md

1217. 玩筹码

English Version

题目描述

有 n 个筹码。第 i 个芯片的位置是 position[i] 。

我们需要把所有筹码移到同一个位置。在一步中，我们可以将第 i 个芯片的位置从 position[i] 改变为:

• position[i] + 2 或 position[i] - 2 ，此时 cost = 0
• position[i] + 1 或 position[i] - 1 ，此时 cost = 1

返回将所有筹码移动到同一位置上所需要的 最小代价 。

 

示例 1：

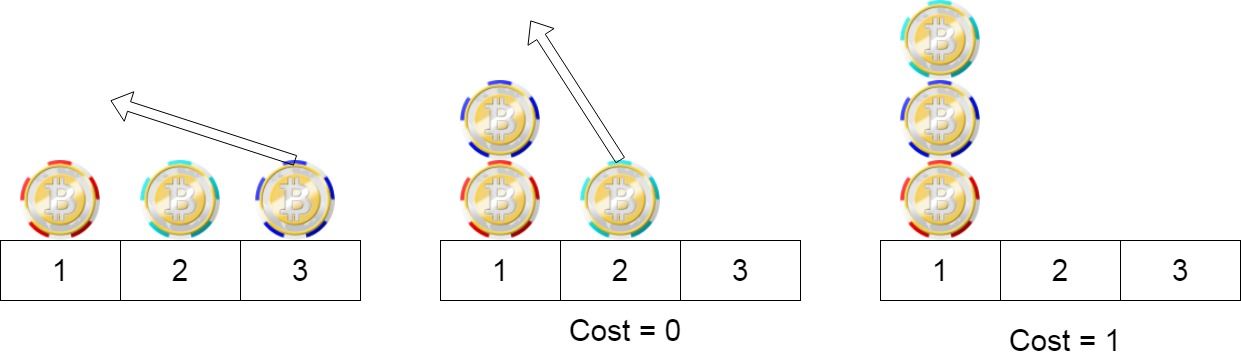
输入：position = [1,2,3]
输出：1
解释：第一步:将位置3的芯片移动到位置1，成本为0。
第二步:将位置2的芯片移动到位置1，成本= 1。
总成本是1。

示例 2：

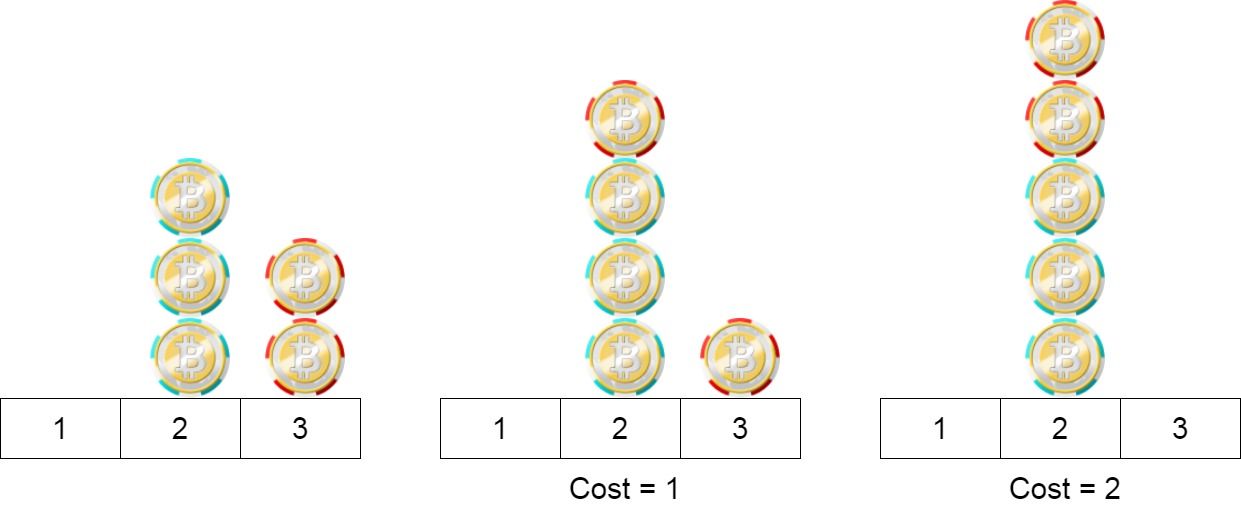
输入：position = [2,2,2,3,3]
输出：2
解释：我们可以把位置3的两个芯片移到位置2。每一步的成本为1。总成本= 2。

示例 3:

输入：position = [1,1000000000]
输出：1

 

提示：

• 1 <= chips.length <= 100
• 1 <= chips[i] <= 10^9

解法

方法一：脑筋急转弯

将所有偶数下标的芯片移动到 0 号位置，所有奇数下标的芯片移动到 1 号位置，所有的代价为 0，接下来只需要在 0/1 号位置中选择其中一个较小数量的芯片，移动到另一个位置。所需的最小代价就是那个较小的数量。

Python3

class Solution:
    def minCostToMoveChips(self, position: List[int]) -> int:
        a = sum(p % 2 for p in position)
        b = len(position) - a
        return min(a, b)

Java

class Solution {
    public int minCostToMoveChips(int[] position) {
        int a = 0;
        for (int p : position) {
            a += p % 2;
        }
        int b = position.length - a;
        return Math.min(a, b);
    }
}

C++

class Solution {
public:
    int minCostToMoveChips(vector<int>& position) {
        int a = 0;
        for (auto& p : position) a += p & 1;
        int b = position.size() - a;
        return min(a, b);
    }
};

Go

func minCostToMoveChips(position []int) int {
	a := 0
	for _, p := range position {
		a += p & 1
	}
	b := len(position) - a
	if a < b {
		return a
	}
	return b
}

...