README.md

1823. 找出游戏的获胜者

English Version

题目描述

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按 顺时针顺序 从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

1. 从第 1 名小伙伴所在位置 开始 。
2. 沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
3. 你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
4. 如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
5. 否则，圈子中最后一名小伙伴赢得游戏。

给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

 

示例 1：

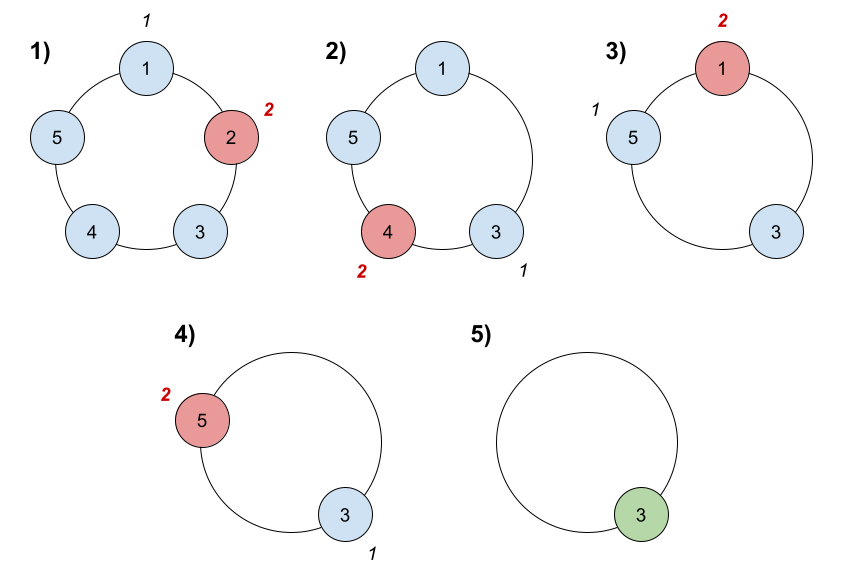
输入：n = 5, k = 2
输出：3
解释：游戏运行步骤如下：
1) 从小伙伴 1 开始。
2) 顺时针数 2 名小伙伴，也就是小伙伴 1 和 2 。
3) 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
4) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 4 。
5) 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
6) 顺时针数 2 名小伙伴，也就是小伙伴 5 和 1 。
7) 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
8) 顺时针数 2 名小伙伴，也就是小伙伴 3 和 5 。
9) 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。

示例 2：

输入：n = 6, k = 5
输出：1
解释：小伙伴离开圈子的顺序：5、4、6、2、3 。小伙伴 1 是游戏的获胜者。

 

提示：

• 1 <= k <= n <= 500

 

进阶：你能否使用线性时间复杂度和常数空间复杂度解决此问题？

解法

约瑟夫环。

Python3

class Solution:
    def findTheWinner(self, n: int, k: int) -> int:
        if n == 1:
            return 1
        ans = (k + self.findTheWinner(n - 1, k)) % n
        return n if ans == 0 else ans

Java

class Solution {
    public int findTheWinner(int n, int k) {
        if (n == 1) {
            return 1;
        }
        int ans = (findTheWinner(n - 1, k) + k) % n;
        return ans == 0 ? n : ans;
    }
}

C++

class Solution {
public:
    int findTheWinner(int n, int k) {
        if (n == 1) return 1;
        int ans = (findTheWinner(n - 1, k) + k) % n;
        return ans == 0 ? n : ans;
    }
};

Go

func findTheWinner(n int, k int) int {
	if n == 1 {
		return 1
	}
	ans := (findTheWinner(n-1, k) + k) % n
	if ans == 0 {
		return n
	}
	return ans
}

TypeScript

class LinkNode {
    public val: number;
    public next: LinkNode;

    constructor(val: number = 0, next?: LinkNode) {
        this.val = val;
        this.next = next;
    }
}

function findTheWinner(n: number, k: number): number {
    if (k === 1) {
        return n;
    }
    const dummy = new LinkNode(0);
    let cur = dummy;
    for (let i = 1; i <= n; i++) {
        cur.next = new LinkNode(i);
        cur = cur.next;
    }
    cur.next = dummy.next;

    cur = dummy;
    let count = 0;
    while (cur.next != cur) {
        count++;
        if (count === k) {
            cur.next = cur.next.next;
            count = 0;
        } else {
            cur = cur.next;
        }
    }
    return cur.val;
}

...