Skip to content

Latest commit

 

History

History
272 lines (223 loc) · 9.01 KB

README.md

File metadata and controls

272 lines (223 loc) · 9.01 KB
Raw

1368. 使网格图至少有一条有效路径的最小代价

English Version

题目描述

给你一个 m x n 的网格图 grid 。 grid 中每个格子都有一个数字，对应着从该格子出发下一步走的方向。 grid[i][j] 中的数字可能为以下几种情况：

  • 1 ，下一步往右走，也就是你会从 grid[i][j] 走到 grid[i][j + 1]
  • 2 ，下一步往左走，也就是你会从 grid[i][j] 走到 grid[i][j - 1]
  • 3 ，下一步往下走，也就是你会从 grid[i][j] 走到 grid[i + 1][j]
  • 4 ，下一步往上走，也就是你会从 grid[i][j] 走到 grid[i - 1][j]

注意网格图中可能会有 无效数字 ，因为它们可能指向 grid 以外的区域。

一开始，你会从最左上角的格子 (0,0) 出发。我们定义一条 有效路径 为从格子 (0,0) 出发，每一步都顺着数字对应方向走，最终在最右下角的格子 (m - 1, n - 1) 结束的路径。有效路径 不需要是最短路径 。

你可以花费 cost = 1 的代价修改一个格子中的数字，但每个格子中的数字 只能修改一次 。

请你返回让网格图至少有一条有效路径的最小代价。

 

示例 1：

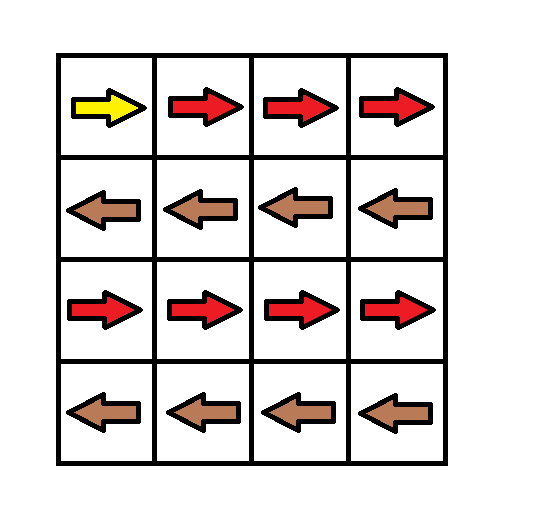
输入：grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
输出：3
解释：你将从点 (0, 0) 出发。
到达 (3, 3) 的路径为： (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) 花费代价 cost = 1 使方向向下 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) 花费代价 cost = 1 使方向向下 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) 花费代价 cost = 1 使方向向下 --> (3, 3)
总花费为 cost = 3.

示例 2：

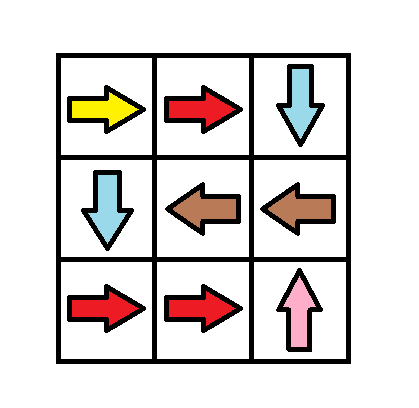
输入：grid = [[1,1,3],[3,2,2],[1,1,4]]
输出：0
解释：不修改任何数字你就可以从 (0, 0) 到达 (2, 2) 。

示例 3：

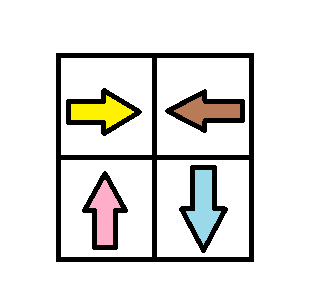
输入：grid = [[1,2],[4,3]]
输出：1

示例 4：

输入：grid = [[2,2,2],[2,2,2]]
输出：3

示例 5：

输入：grid = [[4]]
输出：0

 

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 100

解法

方法一：双端队列 BFS

本题实际上也是最短路模型，只不过求解的是改变方向的最小次数。

在一个边权只有 0、1 的无向图中搜索最短路径可以使用双端队列进行 BFS。其原理是当前可以扩展到的点的权重为 0 时，将其加入队首；权重为 1 时，将其加入队尾。

如果某条边权值为 0，那么新拓展出的节点权值就和当前队首节点权值相同，显然可以作为下一次拓展的起点。

Python3

class Solution:
    def minCost(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        dirs = [[0, 0], [0, 1], [0, -1], [1, 0], [-1, 0]]
        q = deque([(0, 0, 0)])
        vis = set()
        while q:
            i, j, d = q.popleft()
            if (i, j) in vis:
                continue
            vis.add((i, j))
            if i == m - 1 and j == n - 1:
                return d
            for k in range(1, 5):
                x, y = i + dirs[k][0], j + dirs[k][1]
                if 0 <= x < m and 0 <= y < n:
                    if grid[i][j] == k:
                        q.appendleft((x, y, d))
                    else:
                        q.append((x, y, d + 1))
        return -1

Java

class Solution {
    public int minCost(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        boolean[][] vis = new boolean[m][n];
        Deque<int[]> q = new ArrayDeque<>();
        q.offer(new int[]{0, 0, 0});
        int[][] dirs = {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1], d = p[2];
            if (i == m - 1 && j == n - 1) {
                return d;
            }
            if (vis[i][j]) {
                continue;
            }
            vis[i][j] = true;
            for (int k = 1; k <= 4; ++k) {
                int x = i + dirs[k][0], y = j + dirs[k][1];
                if (x >= 0 && x < m && y >= 0 && y < n) {
                    if (grid[i][j] == k) {
                        q.offerFirst(new int[]{x, y, d});
                    } else {
                        q.offer(new int[]{x, y, d + 1});
                    }
                }
            }
        }
        return -1;
    }
}

TypeScript

function minCost(grid: number[][]): number {
    const m = grid.length,
        n = grid[0].length;
    let ans = Array.from({ length: m }, v => new Array(n).fill(Infinity));
    ans[0][0] = 0;
    let queue = [[0, 0]];
    const dirs = [
        [0, 1],
        [0, -1],
        [1, 0],
        [-1, 0],
    ];
    while (queue.length) {
        let [x, y] = queue.shift();
        for (let step = 1; step < 5; step++) {
            let [dx, dy] = dirs[step - 1];
            let [i, j] = [x + dx, y + dy];
            if (i < 0 || i >= m || j < 0 || j >= n) continue;
            let cost = ~~(grid[x][y] != step) + ans[x][y];
            if (cost >= ans[i][j]) continue;
            ans[i][j] = cost;
            if (grid[x][y] == step) {
                queue.unshift([i, j]);
            } else {
                queue.push([i, j]);
            }
        }
    }
    return ans[m - 1][n - 1];
}

C++

class Solution {
public:
    int minCost(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<bool>> vis(m, vector<bool>(n));
        vector<vector<int>> dirs = {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};
        deque<pair<int, int>> q;
        q.push_back({0, 0});
        while (!q.empty())
        {
            auto p = q.front();
            q.pop_front();
            int i = p.first / n, j = p.first % n, d = p.second;
            if (i == m - 1 && j == n - 1) return d;
            if (vis[i][j]) continue;
            vis[i][j] = true;
            for (int k = 1; k <= 4; ++k)
            {
                int x = i + dirs[k][0], y = j + dirs[k][1];
                if (x >= 0 && x < m && y >= 0 && y < n)
                {
                    if (grid[i][j] == k) q.push_front({x * n + y, d});
                    else q.push_back({x * n + y, d + 1});
                }
            }
        }
        return -1;
    }
};

Go

func minCost(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	q := doublylinkedlist.New()
	q.Add([]int{0, 0, 0})
	dirs := [][]int{{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}}
	vis := make([][]bool, m)
	for i := range vis {
		vis[i] = make([]bool, n)
	}
	for !q.Empty() {
		v, _ := q.Get(0)
		p := v.([]int)
		q.Remove(0)
		i, j, d := p[0], p[1], p[2]
		if i == m-1 && j == n-1 {
			return d
		}
		if vis[i][j] {
			continue
		}
		vis[i][j] = true
		for k := 1; k <= 4; k++ {
			x, y := i+dirs[k][0], j+dirs[k][1]
			if x >= 0 && x < m && y >= 0 && y < n {
				if grid[i][j] == k {
					q.Insert(0, []int{x, y, d})
				} else {
					q.Add([]int{x, y, d + 1})
				}
			}
		}
	}
	return -1
}

...