Data Structure and Algorithm Practice for Leetcode
Jovian: Data Structures and Algorithms in Python
Data Structures and Algorithms in Python - Full Course for Beginners
Algorithms and Data Structures Tutorial
This article will be a collection of cheat sheets that you can use as you solve problems and prepare for interviews. You will find:
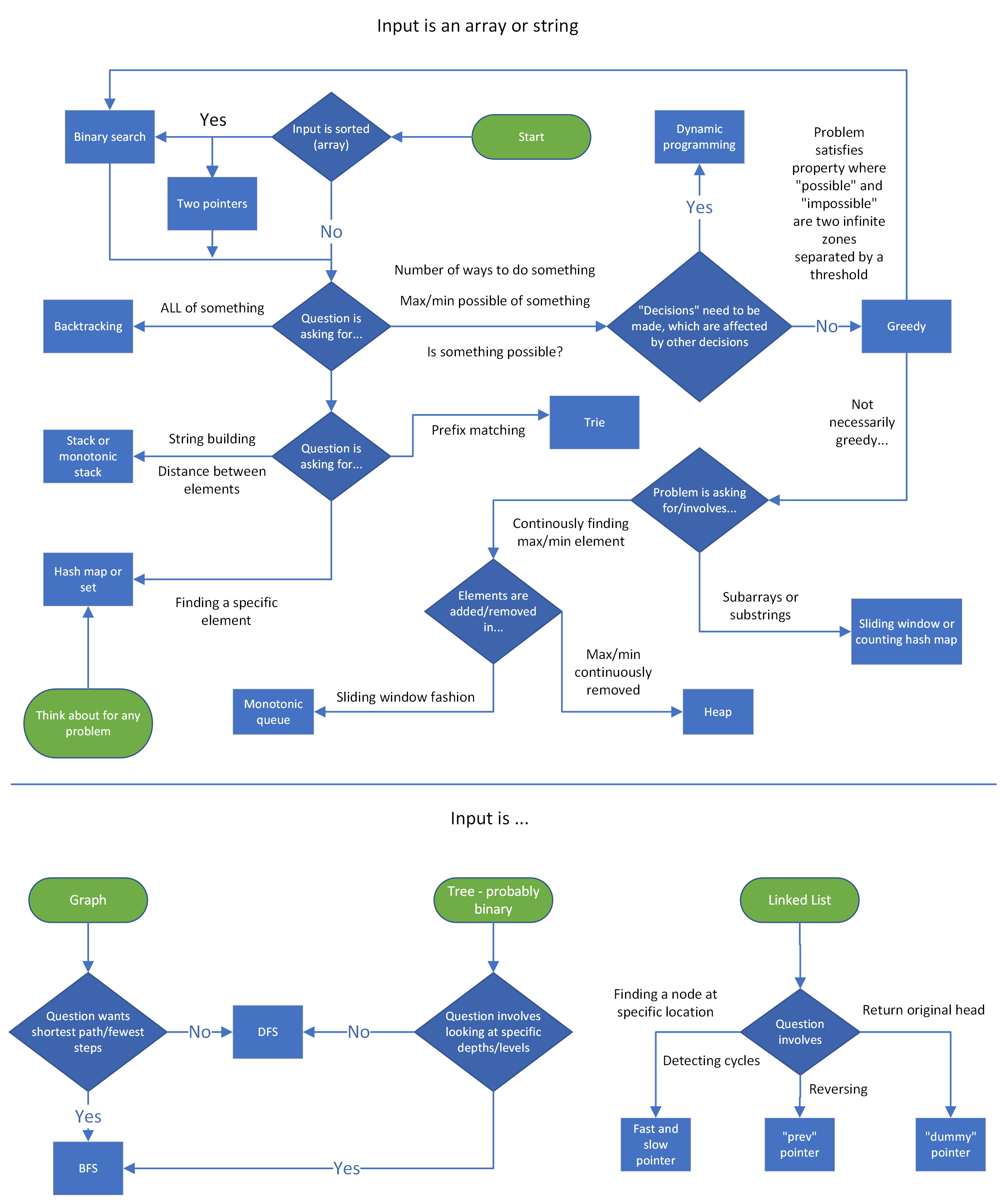
Time complexity (Big O) cheat sheet General DS/A flowchart (when to use each DS/A) Stages of an interview cheat sheet
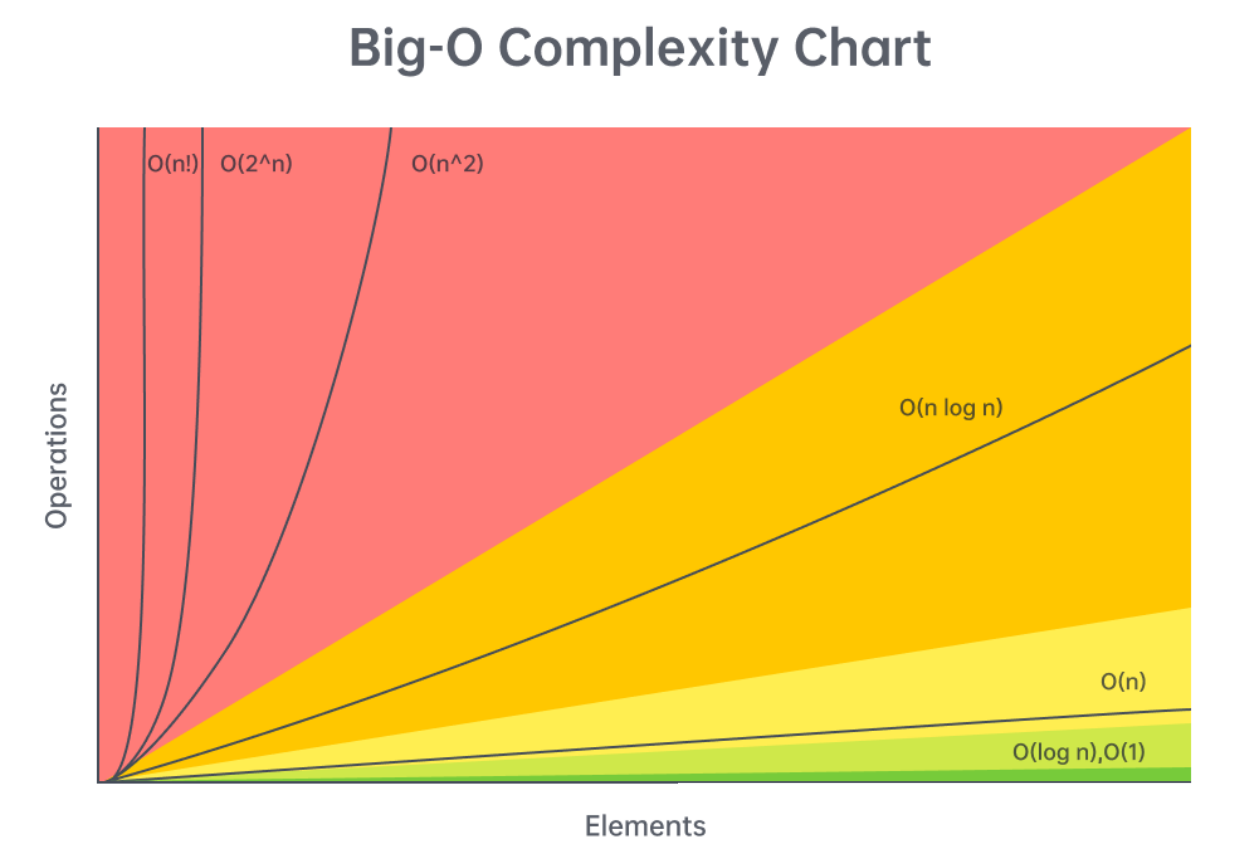 First, let's talk about the time complexity of common operations, split by data structure/algorithm. Then, we'll talk about reasonable complexities given input sizes.
First, let's talk about the time complexity of common operations, split by data structure/algorithm. Then, we'll talk about reasonable complexities given input sizes.
Arrays (dynamic array/list)
Given n = arr.length
| Operation | Time Complexity |
|---|---|
| Add or remove element at the end | O(1) amortized |
| Add or remove element from arbitrary index | O(n) |
| Access or modify element at arbitrary index | O(1) |
| Check if element exists | O(n) |
| Two pointers | O(nk) |
| Building a prefix sum | O(n) |
| Finding the sum of a subarray given a prefix sum | O(1) |
Strings (immutable)
Given n = s.length
| Operation | Time Complexity |
|---|---|
| Add or remove character | O(n) |
| Access element at arbitrary index | O(1) |
| Concatenation between two strings | O(n + m) |
| Create substring | O(m) |
| Two pointers | O(nk) |
| Building a string from joining | O(n) |
Linked Lists
Given n as the number of nodes in the linked list
| Operation | Time Complexity |
|---|---|
| Add or remove element (given pointer) | O(1) |
| Add or remove element (without pointer) | O(n) |
| Access element (without pointer) | O(n) |
| Check if element exists | O(n) |
| Reverse between position i and j | O(j - i) |
| Detect a cycle | O(n) |
Hash Table/Dictionary
Given n = dic.length
| Operation | Time Complexity |
|---|---|
| Add or remove key-value pair | O(1) |
| Check if key exists | O(1) |
| Check if value exists | O(n) |
| Access or modify value associated with key | O(1) |
| Iterate over all keys, values, or both | O(n) |
Set
Given n = set.length
| Operation | Time Complexity |
|---|---|
| Add or remove element | O(1) |
| Check if element exists | O(1) |
Stack
Given n = stack.length
| Operation | Time Complexity |
|---|---|
| Push element | O(1) |
| Pop element | O(1) |
| Peek (see element at top of stack) | O(1) |
| Check if element exists | O(n) |
Queue
Given n = queue.length
| Operation | Time Complexity |
|---|---|
| Enqueue element | O(1) |
| Dequeue element | O(1) |
| Peek (see element at front of queue) | O(1) |
| Check if element exists | O(n) |
Binary Tree (DFS/BFS)
Given n as the number of nodes in the tree
| Operation | Time Complexity |
|---|---|
| Most algorithms | O(nk) |
Binary Search Tree
Given n as the number of nodes in the tree
| Operation | Time Complexity |
|---|---|
| Add or remove element | O(n) (worst), O(logn) (average) |
| Check if element exists | O(n) (worst), O(logn) (average) |
Heap/Priority Queue
Given n = heap.length and talking about min heaps
| Operation | Time Complexity |
|---|---|
| Add an element | O(logn) |
| Delete the minimum element | O(logn) |
| Find the minimum element | O(1) |
| Check if element exists | O(n) |
Binary Search
Given n is the size of your initial search space
| Operation | Time Complexity |
|---|---|
| Binary search | O(logn) |
Note: These time complexities represent the general case and may vary based on specific implementations or optimizations.
Miscellaneous
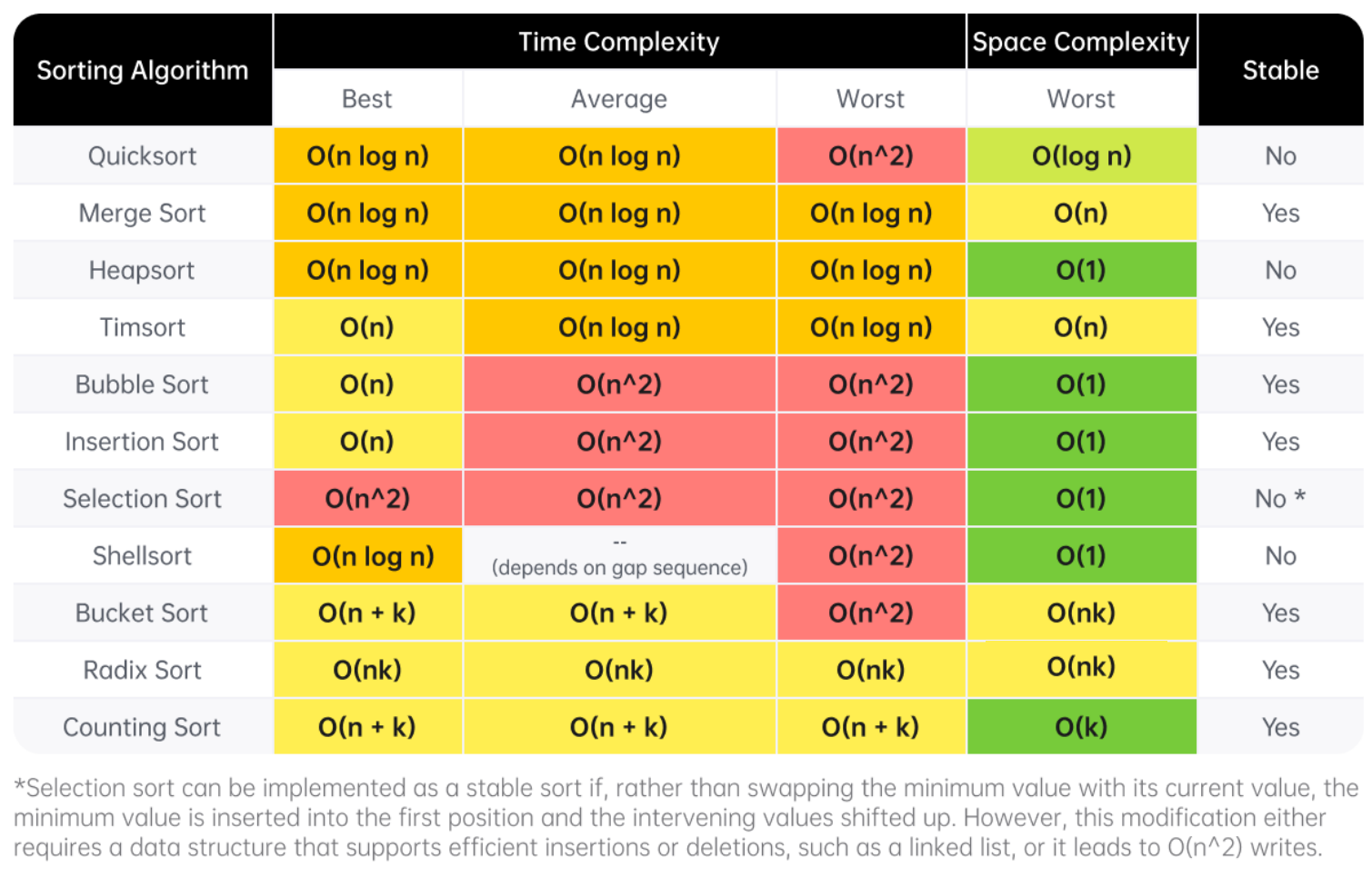
Sorting
n is the size of the data being sorted
| Operation | Time Complexity |
|---|---|
| Sorting | O(n log n) |
DFS and BFS on a Graph
n is the number of nodes, e is the number of edges
| Operation | Time Complexity |
|---|---|
| DFS and BFS | O(nk + e) |
| Space Complexity (Graph) | O(n + e) |
Dynamic Programming
n is the number of states and k is the work done at each state
| Operation | Time Complexity | Space Complexity |
|---|---|---|
| Dynamic Programming | O(nk) | O(n) |
Note: These time and space complexities represent the general case and may vary based on specific implementations or optimizations.