deepcfd.md

DeepCFD(Deep Computational Fluid Dynamics)

=== "模型训练命令"

``` sh
# linux
wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataX.pkl
wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataY.pkl
# windows
# curl -o ./datasets/dataX.pkl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataX.pkl
# curl -o ./datasets/dataX.pkl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataY.pkl
python deepcfd.py
```

1. 背景简介

计算流体力学（Computational fluid dynamics, CFD）模拟通过求解 Navier-Stokes 方程（N-S 方程），可以获得流体的各种物理量的分布，如密度、压力和速度等。在微电子系统、土木工程和航空航天等领域应用广泛。

在某些复杂的应用场景中，如机翼优化和流体与结构相互作用方面，需要使用千万级甚至上亿的网格对问题进行建模（如下图所示，下图展示了 F-18 战斗机的全机内外流一体结构化网格模型），导致 CFD 的计算量非常巨大。因此，目前亟需发展出一种相比于传统 CFD 方法更高效，且可以保持计算精度的方法。

{ loading=lazy} F-18 战斗机的全机内外流一体结构化网格模型

2. 问题定义

Navier-Stokes 方程是用于描述流体运动的方程，它的二维形式如下，

质量守恒：

$$\nabla \cdot \bf{u}=0$$

动量守恒：

$$\rho(\frac{\partial}{\partial t} + \bf{u} \cdot div ) \bf{u} = - \nabla p + - \nabla \tau + \bf{f}$$

其中 $\bf{u}$ 是速度场（具有 x 和 y 两个维度），$\rho$ 是密度， $p$ 是压强场，$\bf{f}$ 是体积力（例如重力）。

假设满足非均匀稳态流体条件，方程可去掉时间相关项，并将 $\bf{u}$ 分解为速度分量 $u_x$ 和 $u_y$ ，动量方程可重写成：

$$u_x\frac{\partial u_x}{\partial x} + u_y\frac{\partial u_x}{\partial y} = - \frac{1}{\rho}\frac{\partial p}{\partial x} + \nu \nabla^2 u_x + g_x$$

$$u_x\frac{\partial u_y}{\partial x} + u_y\frac{\partial u_y}{\partial y} = - \frac{1}{\rho}\frac{\partial p}{\partial y} + \nu \nabla^2 u_y + g_y$$

其中 $g$ 代表重力加速度，$\nu$ 代表流体的动力粘度。

3. 问题求解

上述问题通常可使用 OpenFOAM 进行传统数值方法的求解，但计算量很大，接下来开始讲解如何基于 PaddleScience 代码，用深度学习的方法求解该问题。

本案例基于论文 Ribeiro M D, Rehman A, Ahmed S, et al. DeepCFD: Efficient steady-state laminar flow approximation with deep convolutional neural networks 的方法进行求解，关于该方法的理论部分请参考原论文。 为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 API文档。

3.1 数据集介绍

该数据集中的数据使用 OpenFOAM 求得。数据集有两个文件 dataX 和 dataY。dataX 包含 981 个通道流样本几何形状的输入信息，dataY 包含对应的 OpenFOAM 求解结果。

运行本问题代码前请按照下方命令下载 dataX 和 dataY：

wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataX.pkl
wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepCFD/dataY.pkl

dataX 和 dataY 都具有相同的维度（Ns，Nc，Nx，Ny），其中第一轴是样本数（Ns），第二轴是通道数（Nc），第三和第四轴分别是 x 和 y 中的元素数量（Nx 和 Ny）。在输入数据 dataX 中，第一通道是计算域中障碍物的SDF（Signed distance function），第二通道是流动区域的标签，第三通道是计算域边界的 SDF。在输出数据 dataY 中，第一个通道是水平速度分量（Ux），第二个通道是垂直速度分量（Uy），第三个通道是流体压强（p）。

数据集原始下载地址为：https://zenodo.org/record/3666056/files/DeepCFD.zip?download=1

我们将数据集以 7:3 的比例划分为训练集和验证集，代码如下：

--8<--
examples/deepcfd/deepcfd.py:202:216
--8<--

3.2 模型构建

在上述问题中，我们确定了输入为 input，输出为 output，按照论文所述，我们使用含有 3 个 encoder 和 decoder 的 UNetEx 网络来创建模型。

模型的输入包含了障碍物的 SDF（Signed distance function）、流动区域的标签以及计算域边界的 SDF。模型的输出包含了水平速度分量（Ux），垂直速度分量（Uy）以及流体压强（p）。

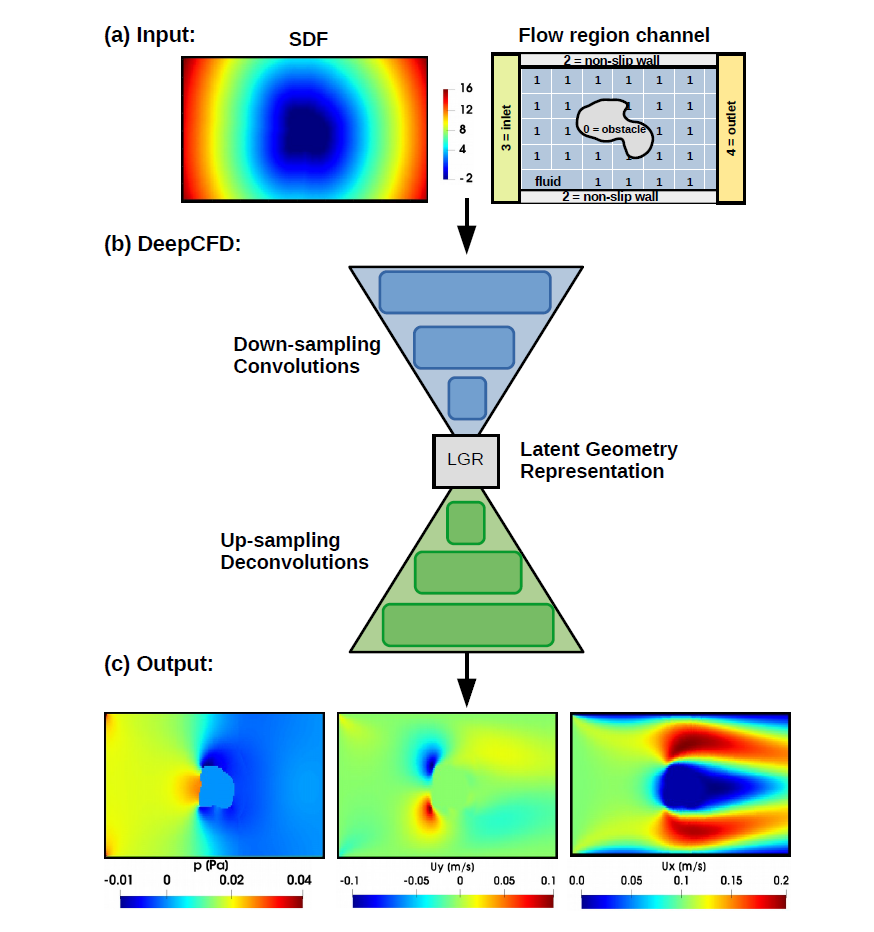{ loading=lazy} DeepCFD网络结构

模型创建用 PaddleScience 代码表示如下：

--8<--
examples/deepcfd/deepcfd.py:218:219
--8<--

3.3 约束构建

本案例基于数据驱动的方法求解问题，因此需要使用 PaddleScience 内置的 SupervisedConstraint 构建监督约束。在定义约束之前，需要首先指定监督约束中用于数据加载的各个参数，代码如下：

--8<--
examples/deepcfd/deepcfd.py:234:264
--8<--

SupervisedConstraint 的第一个参数是数据的加载方式，这里填入相关数据的变量名。

第二个参数是损失函数的定义，这里使用自定义的损失函数，分别计算 Ux 和 Uy 的均方误差，以及 p 的标准差，然后三者加权求和。

第三个参数是约束条件的名字，方便后续对其索引。此次命名为 "sup_constraint"。

在监督约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。

--8<--
examples/deepcfd/deepcfd.py:266:267
--8<--

3.4 超参数设定

接下来需要在配置文件中指定训练轮数，此处我们按实验经验，使用一千轮训练轮数。

--8<--
examples/deepcfd/conf/deepcfd.yaml:47:52
--8<--

3.5 优化器构建

训练过程会调用优化器来更新模型参数，此处选择较为常用的 Adam 优化器，学习率设置为 0.001，权重衰减设置为 0.005。

--8<--
examples/deepcfd/deepcfd.py:269:272
--8<--

3.6 评估器构建

在训练过程中通常会按一定轮数间隔，用验证集评估当前模型的训练情况，我们使用 ppsci.validate.SupervisedValidator 构建评估器。

--8<--
examples/deepcfd/deepcfd.py:274:314
--8<--

评价指标 metric 这里自定义了四个指标 Total_MSE、Ux_MSE、Uy_MSE 和 p_MSE。

其余配置与 约束构建 的设置类似。

3.7 模型训练、评估

完成上述设置之后，只需要将上述实例化的对象按顺序传递给 ppsci.solver.Solver，然后启动训练、评估。

--8<--
examples/deepcfd/deepcfd.py:316:335
--8<--

3.8 结果可视化

使用 matplotlib 绘制相同输入参数时的 OpenFOAM 和 DeepCFD 的计算结果，进行对比。这里绘制了验证集第 0 个数据的计算结果。

--8<--
examples/deepcfd/deepcfd.py:337:342
--8<--

4. 完整代码

--8<--
examples/deepcfd/deepcfd.py
--8<--

5. 结果展示

{ loading=lazy} OpenFOAM 计算结果与 DeepCFD 预测结果对比，从上到下分别为：水平速度分量（Ux），垂直速度分量（Uy）以及流体压强（p）

可以看到DeepCFD方法与OpenFOAM的结果基本一致。

6. 参考文献

• Ribeiro M D, Rehman A, Ahmed S, et al. DeepCFD: Efficient steady-state laminar flow approximation with deep convolutional neural networks
• 基于PaddlePaddle的DeepCFD复现