volterra_ide.md

Volterra integral equation

AI Studio快速体验

=== "模型训练命令"

``` sh
python volterra_ide.py
```

=== "模型评估命令"

``` sh
python volterra_ide.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/volterra_ide/volterra_ide_pretrained.pdparams
```

预训练模型	指标
volterra_ide_pretrained.pdparams	loss(L2Rel_Validator): 0.00023 L2Rel.u(L2Rel_Validator): 0.00023

1. 背景简介

Volterra integral equation(沃尔泰拉积分方程)是一种积分方程，即方程中含有对待求解函数的积分运算，其有两种形式，如下所示

$$ \begin{aligned} f(t) &= \int_a^t K(t, s) x(s) d s \\ x(t) &= f(t)+\int_a^t K(t, s) x(s) d s \end{aligned} $$

在数学领域，沃尔泰拉方程可以用于表达各种多变量概率分布，是进行多变量统计分析的有力工具。这使得它在处理复杂数据结构时非常有用，例如在机器学习领域。沃尔泰拉方程还可以用于计算不同维度属性的相关性，以及模拟复杂的数据集结构，以便为机器学习任务提供有效的数据支持。

在生物学领域，沃尔泰拉方程被用作渔业生产的指导，对生态平衡和环境保护有重要意义。此外，该方程还在疾病防治，人口统计等方面有应用。值得一提的是，沃尔泰拉方程的建立是数学在生物学领域应用的首次成功尝试，推动了生物数学这门科学的产生和发展。

本案例以第二种方程为例，使用深度学习的方式进行求解。

2. 问题定义

假设存在如下 IDE 方程：

$$ u(t) = -\dfrac{du}{dt} + \int_{t_0}^t e^{t-s} u(s) d s $$

其中 $u(t)$ 就是待求解的函数，而 $-\dfrac{du}{dt}$ 对应了 $f(t)$，$e^{t-s}$ 对应了 $K(t,s)$。 因此可以利用神经网络模型，以 $t$ 为输入，$u(t)$ 为输出，根据上述方程构建微分约束，进行无监督学习最终拟合出待求解的函数 $u(t)$。

为了方便在计算机中进行求解，我们将上式进行移项，让积分项作为左侧，非积分项放至右侧，如下所示：

$$ \int_{t_0}^t e^{t-s} u(s) d s = u(t) + \dfrac{du}{dt} $$

3. 问题求解

接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。 为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 API文档。

3.1 模型构建

在上述问题中，我们确定了输入为 $x$，输出为 $u(x)$，因此我们使用，用 PaddleScience 代码表示如下：

--8<--
examples/ide/volterra_ide.py:39:40
--8<--

为了在计算时，准确快速地访问具体变量的值，我们在这里指定网络模型的输入变量名是 "x"(即公式中的 $t$)，输出变量名是 "u"，接着通过指定 MLP 的隐藏层层数、神经元个数，我们就实例化出了神经网络模型 model。

3.2 计算域构建

Volterra_IDE 问题的积分域是 $a$ ~ $t$，其中 a 为固定常数 0，t 的范围为 0 ~ 5，因此可以使用PaddleScience 内置的一维几何 TimeDomain 作为计算域。

--8<--
examples/ide/volterra_ide.py:42:43
--8<--

3.3 方程构建

由于 Volterra_IDE 使用的是积分方程，因此可以直接使用 PaddleScience 内置的 ppsci.equation.Volterra，并指定所需的参数：积分下限 a、t 的离散取值点数 num_points、一维高斯积分点的个数 quad_deg、$K(t,s)$ 核函数 kernel_func、$u(t) - f(t)$ 等式右侧表达式 func。

--8<--
examples/ide/volterra_ide.py:45:61
--8<--

3.4 约束构建

3.4.1 内部点约束

本文采用无监督学习的方式，对移项后方程的左、右两侧进行约束，让其尽量相等。

由于等式左侧涉及到积分计算（实际采用高斯积分近似计算），因此在 0 ~ 5 区间内采样出多个 t_i 点后，还需要计算其用于高斯积分的点集，即对每一个 (0,t_i) 区间，都计算出一一对应的高斯积分点集 quad_i 和点权 weight_i。PaddleScience 将这一步作为输入数据的预处理，加入到代码中，如下所示

--8<--
examples/ide/volterra_ide.py:63:117
--8<--

3.4.2 初值约束

在 $t=0$ 时，有以下初值条件：

$$ u(0) = e^{-t} \cosh(t)|_{t=0} = e^{0} \cosh(0) = 1 $$

因此可以加入 t=0 时的初值条件，代码如下所示

--8<--
examples/ide/volterra_ide.py:119:137
--8<--

在微分方程约束、初值约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。

--8<--
examples/ide/volterra_ide.py:138:142
--8<--

3.5 超参数设定

接下来我们需要指定训练轮数和学习率，此处我们按实验经验，让 L-BFGS 优化器进行一轮优化即可，但一轮优化内的 max_iters 数可以设置为一个较大的一个数 15000。

--8<--
examples/ide/conf/volterra_ide.yaml:39:57
--8<--

3.6 优化器构建

训练过程会调用优化器来更新模型参数，此处选择较为常用的 LBFGS 优化器。

--8<--
examples/ide/volterra_ide.py:144:145
--8<--

3.7 评估器构建

在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 ppsci.validate.GeometryValidator 构建评估器。

--8<--
examples/ide/volterra_ide.py:147:161
--8<--

评价指标 metric 选择 ppsci.metric.L2Rel 即可。

其余配置与 3.4 约束构建 的设置类似。

3.8 模型训练

完成上述设置之后，只需要将上述实例化的对象按顺序传递给 ppsci.solver.Solver，然后启动训练。

--8<--
examples/ide/volterra_ide.py:163:181
--8<--

3.9 结果可视化

在模型训练完毕之后，我们可以手动构造 0 ~ 5 区间内均匀 100 个点，作为评估的积分上限 t 进行预测，并可视化结果。

--8<--
examples/ide/volterra_ide.py:183:194
--8<--

4. 完整代码

--8<--
examples/ide/volterra_ide.py
--8<--

5. 结果展示

模型预测结果如下所示，$t$为自变量，$u(t)$为积分方程标准解函数，$\hat{u}(t)$为模型预测的积分方程解函数

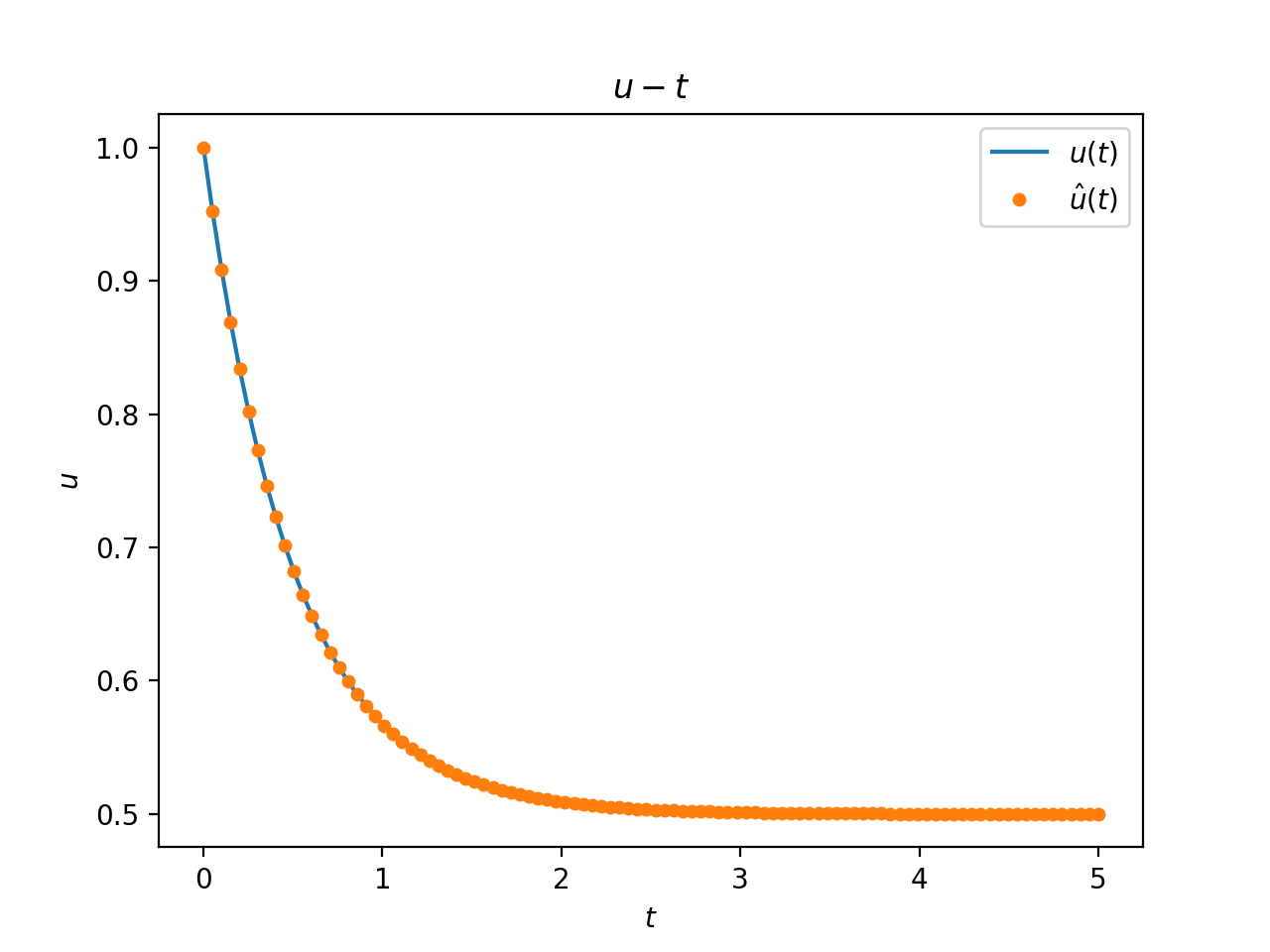{ loading=lazy } 模型求解结果(橙色散点)和参考结果(蓝色曲线)

可以看到模型对积分方程在$[0,5]$区间内的预测结果$\hat{u}(t)$和标准解结果$u(t)$基本一致。

6. 参考文献

• DeepXDE - Antiderivative operator from an unaligned dataset
• Gaussian quadrature
• Volterra integral equation