Learn radiative transfer like it's 1992!
Lightspinner is a relatively simple, but complete pure python optically thick radiative transfer (RT) code using the Rybicki-Hummer Multi-level Accelerated Lambda Iteration (MALI) formalism. It is, in essence, a stripped down version of Lightweaver with the aim of teaching the methods used in optically thick RT and making them more accessible. That is, if you learn methods by reading code, like I do. It uses the full preconditioning method of Rybicki & Hummer (1992) with the ability to handle overlapping transitions, but under the assumption of complete redistribution. The formal solver is currently using simple piecewise linear short characteristics due to its simplicity and the pedagogic benefits thereof.
The slides for the associated talk are in the Slides directory.
In the file response_fn.py there is a simple example of computing the NLTE response function for CaII 8542, admittedly in a very crude and slow way (it will take multiple minutes to run). I recommend just running the synthesis in example.py first for familiarity with the code.
If you want to have a go at implementing the MALI method, then the formal_sol_gamma_matrices and uv functions in rh_method.py have been left documented but not complete on the DIY branch. It would also be an interesting exercise to extend the formal solver to use the monotonic piecewise parabolic method of Auer & Paletou (1994).
Requires python 3.7+.
For those that use conda the environment.yml can be used to create a Lightspinner environment complete with all necessary packages with conda env create -f environment.yml.
This can then be activated with conda activate Lightspinner.
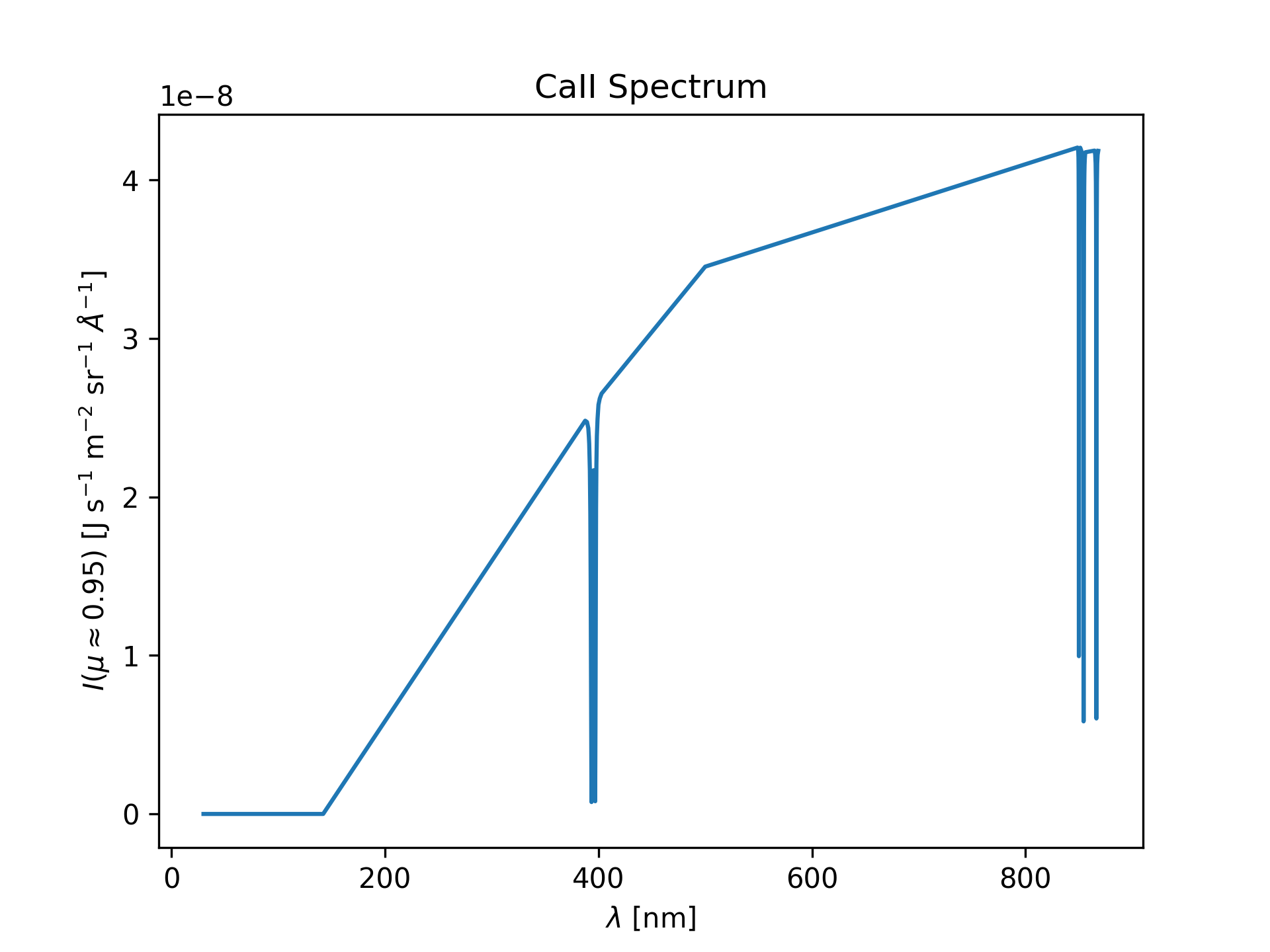
This environment should then be ready for action and you should be able to easily produce the spectrum of Ca II in a FALC atmosphere with ipython -i test.py. It should look like this:
- [HM] Hubeny, Ivan & Mihalas, Dimitri (2015). Theory of Stellar Atmospheres: An Introduction to Astrophysical Non-equilibrium Quantitive Spectroscopic Analysis. Princeton University Press. ISBN: 9780691163291.
- [RH91] Rybicki, G. B.; Hummer D. G. (1991). A&A, 245, 171-181
- [RH92] Rybicki, G. B.; Hummer D. G. (1992). A&A, 262, 209-215
- [U01] Uitenbroek, H. (2001). ApJ, 557, 389-398
- The python implementation of the Wittmann equation of state kindly provided J. de la Cruz Rodriguez.
- Many methods are inspired by approaches taken in the RH code by H. Uitenbroek [U01] (linked version is the 1.5D version described in Pereira & Uitenbroek (2015))
- Many thanks to Ivan Milić for all his help getting this stuff into my head!