MPC gait generation

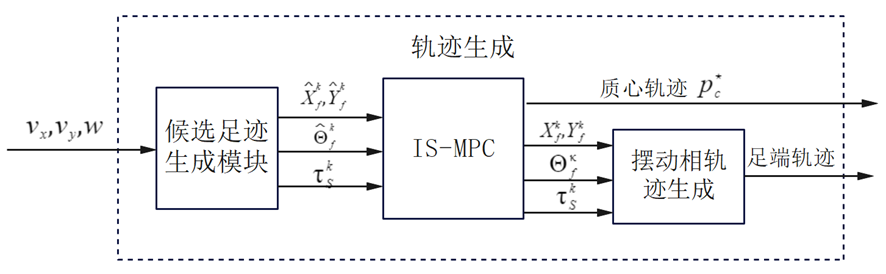
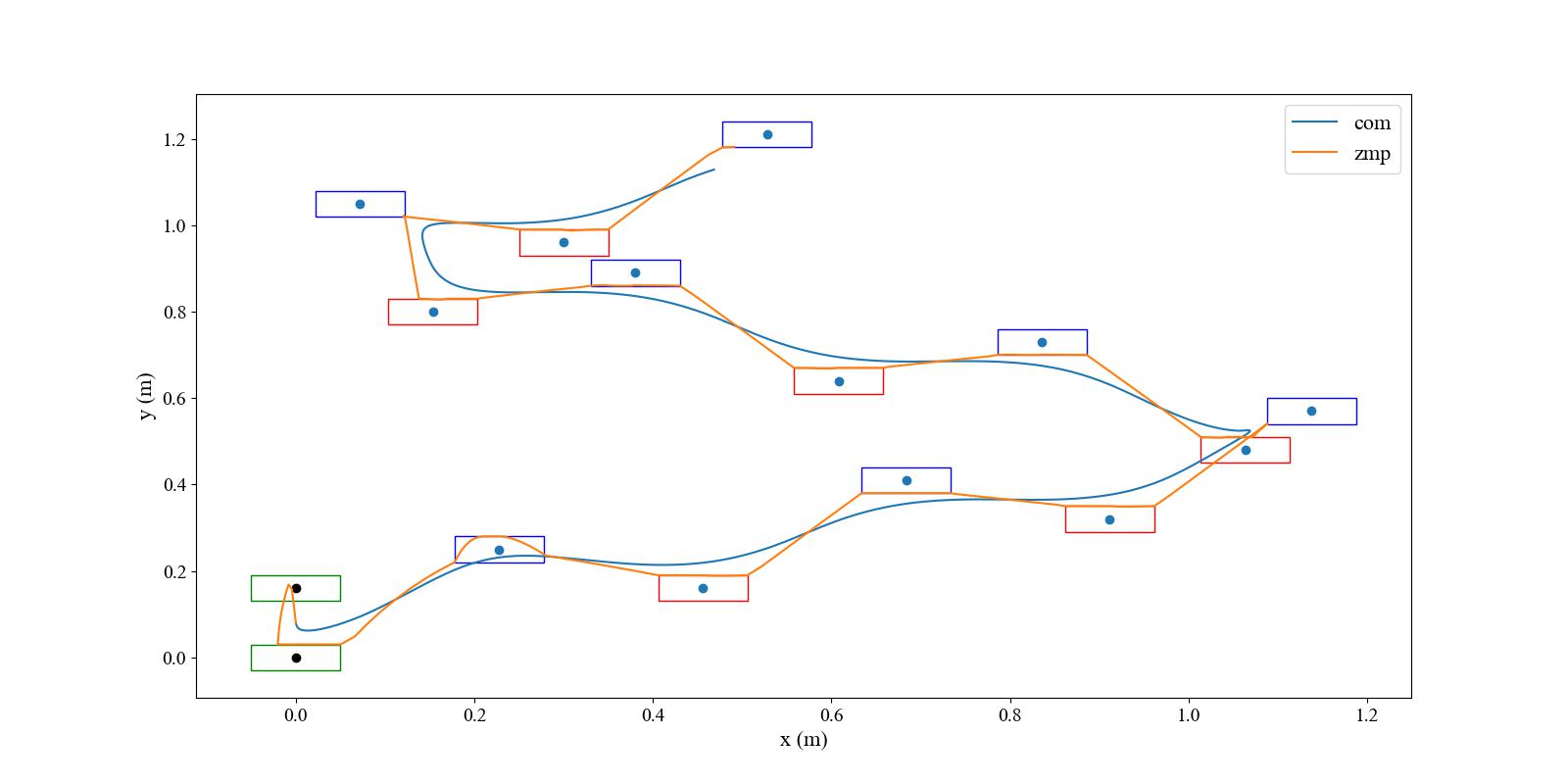
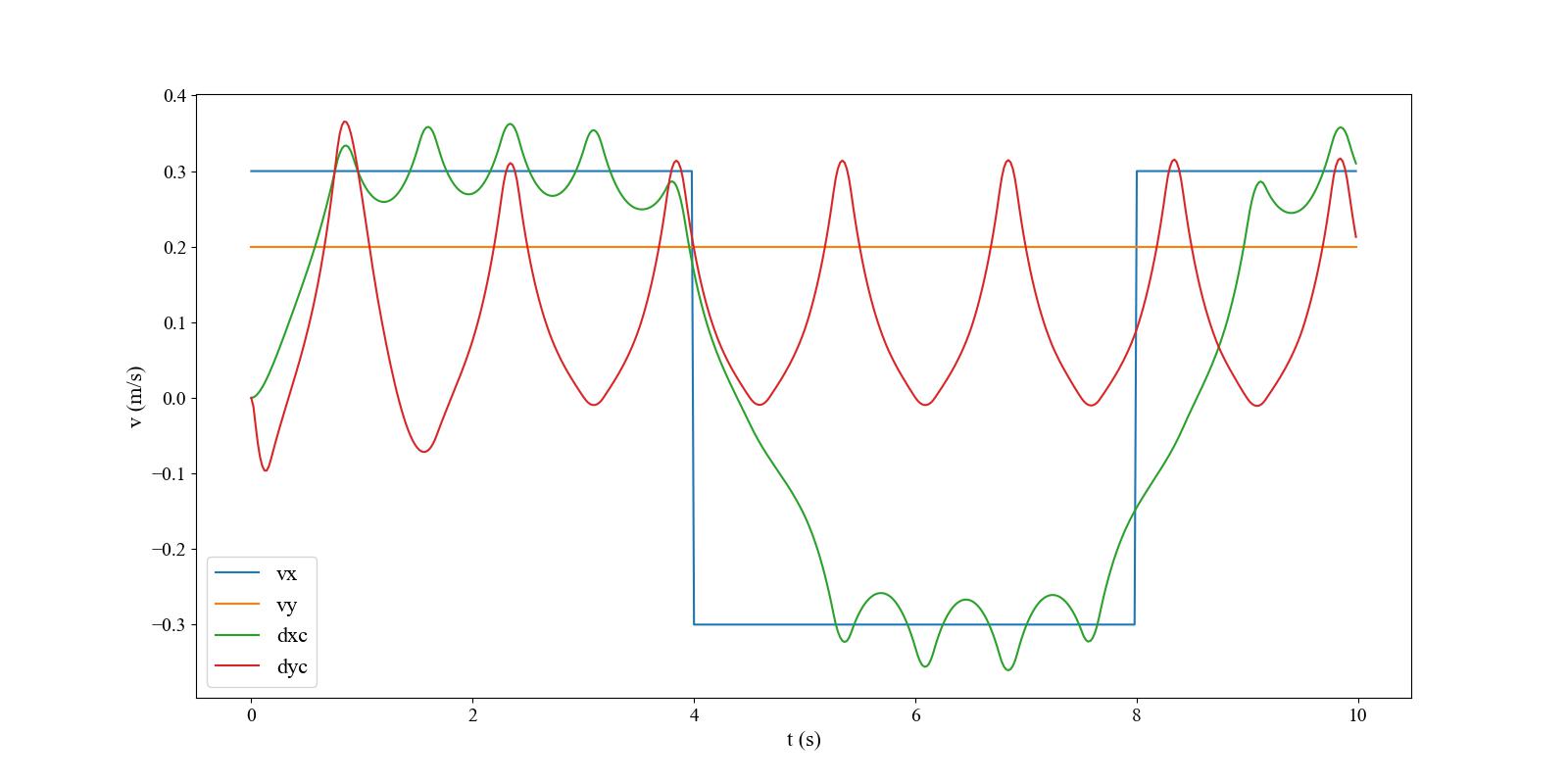
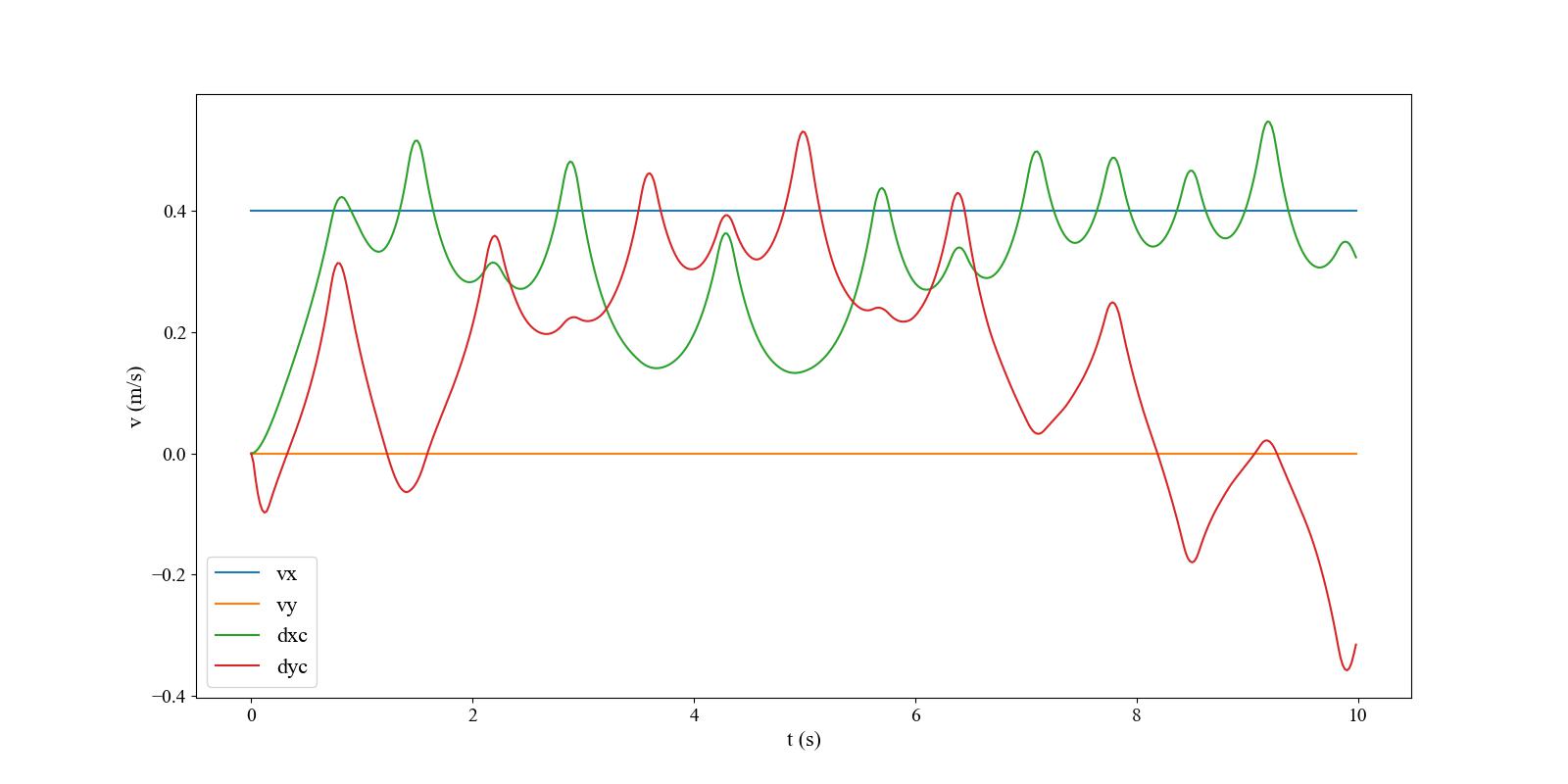
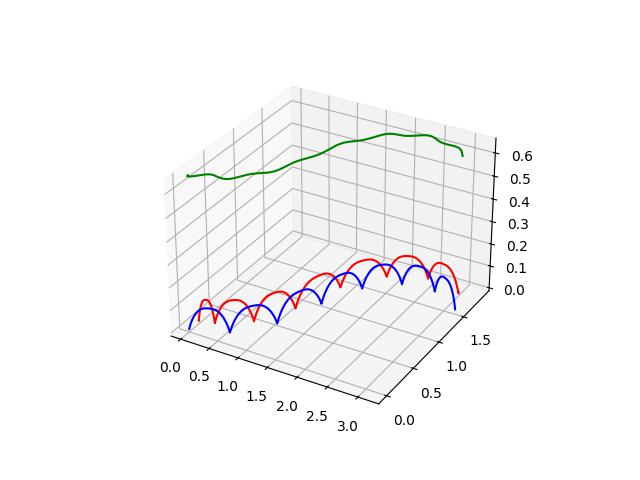
This repository is an implementation in python code of the MPC gait generation described in the "MPC for Humanoid Gait Generation: Stability and Feasibility"

Requirements

matplotlib ​numpy ​scipy ​qpsolvers

Control Framework

QP problem

$$ \min_{\begin{array}{c}\dot{X}_z^k,\dot{Y}_z\X_f,Y_f\end{array}}|\dot{X}_z^k|^2+|\dot{Y}_z^k|^2+\beta(|X_f-\hat{X}_f|^2+|Y_f-\hat{Y}_f|^2) $$ Constrains:Kinematic Constrains,ZMP Position Constrains,Stability Constraint and ZMP Velocity Constraint

Constrains

Kinematic Constrains

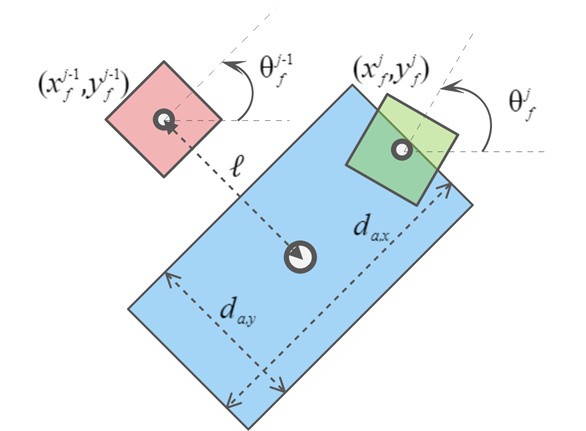
$$ \pm\binom0\ell-\frac12\binom{d_{a,x}}{d_{a,y}}\leq R_{j-1}^T\binom{\hat{x}_f^j-\hat{x}_f^{j-1}}{\hat{y}f^j-\hat{y}f^{j-1}}\leq\pm\binom0\ell+\frac12\binom{d{a,x}}{d{a,y}} $$

ZMP Position Constrains

Single Support

$$ -\frac12\binom{d_{z,x}}{d_{z,y}}\leq R_j^T\begin{pmatrix}\Delta t\sum_{l=0}^i\dot{x}z^{k+l}-x_f^j\\\Delta t\sum{l=0}^i\dot{y}z^{k+l}-y_f^j\end{pmatrix}+R_j^T\begin{pmatrix}x_z^k\y_z^k\end{pmatrix}\leq\frac12\binom{d{z,x}}{d_{z,y}} $$

Double Support(moving constrains)

$$ x_{mc}(t)=\left(1-\alpha^j(t)\right)x_f^j+\alpha^j(t)x_f^{j+1} \
y_{mc}(t)=\left(1-\alpha^j(t)\right)y_f^j+\alpha^j(t)y_f^{j+1} \
\theta_{mc}(t)=\left(1-\alpha^j(t)\right)x_f^j+\alpha^j(t)\theta_f^{j+1} \
\alpha^j(t)=\frac{t-t_s^j}{T_{ds}^j},t\in[t_s^j,t_s^j+T_{ds}^j] $$ and $$ -\frac{1}{2}\binom{d_{z,x}}{d_{z,y}}\leq R_{mc}^T\begin{pmatrix}\Delta t\sum_{l=0}^i\dot{x}z^{k+l}-x{mc}^i\\\Delta t\sum_{l=0}^i\dot{y}z^{k+l}-y{mc}^i\end{pmatrix}+R_{mc}^T\begin{pmatrix}x_z^k\y_z^k\end{pmatrix}\leq\frac{1}{2}\binom{d_{z,x}}{d_{z,y}} $$

Stability Constraint

$$ \sum_{i=0}^{C-1}e^{-i\eta\delta}\dot{x}z^{k+i}=-\sum{i=C}^\infty e^{-i\eta\delta}\dot{x}_z^{k+i}+\frac\eta{1-e^{-\eta\delta}}(x_u^k-x_z^k) $$

ZMP Velocity Constraint

$$ |\dot{x}_z|\leq v^{max},|\dot{y}_z|\leq v^{max} $$

Results

simulation 1

### simulation 2

### simulation 3