This repo contains my notes from Andrej Karpathy's lectures.

0. Concepts to start with

---
title: Learning map
---
flowchart TB
    id1[function backpropagation + activation] --> id2[neuron backprop] --> id3["NN backprop + loss function (update gradient every step)"]

Loading

Lectures

1. bigram_model: using a simple bigram model to generate text

see notebook here

• loss function: negative log likelihood
• not a good model, the names produced does not resemble "names"

2. a very simple NN: using a neural network to generate text

see notebook here

• We see similar results compared to first because NN is very simple

3. MLP

see notebook here and here

• lit: A Neural Probabilistic Language Model
  • 17000 vocab associated with a point in vector space (30 features eg)
  • components:
    • lookup table: C 17000 x 30
    • index of incoming word
    • input layer: 90 neurons total (30 neurons for 3 words)
    • hidden layer: arbitrary number of neurons (100 neurons)
      • hyperparameter (this term means can be as large as you want)
      • fully connected with input layer
    • tanh activation function
    • output layer (expensive layer: also fully connected with hidden layer)
    • softmax (exponentiated, normalized)
    • pluck out probability of word and compare to actual word
    • backpropagation optimization

Part 3 video notes

see here

The initial loss is too high

we would expect uniform distribution of next-letter probability, i.e. log of 1/27

• the shape of the loss looks like a hockey stick
• the initial iterations are squashing down the logits

W2 = torch.randn((n_hidden, vocab_size),          generator=g) * 0.01
b2 = torch.randn(vocab_size,                      generator=g) * 0

• Note W2 cannot be all 0!
• the multiplier = the value of the sd of W2

Tanh

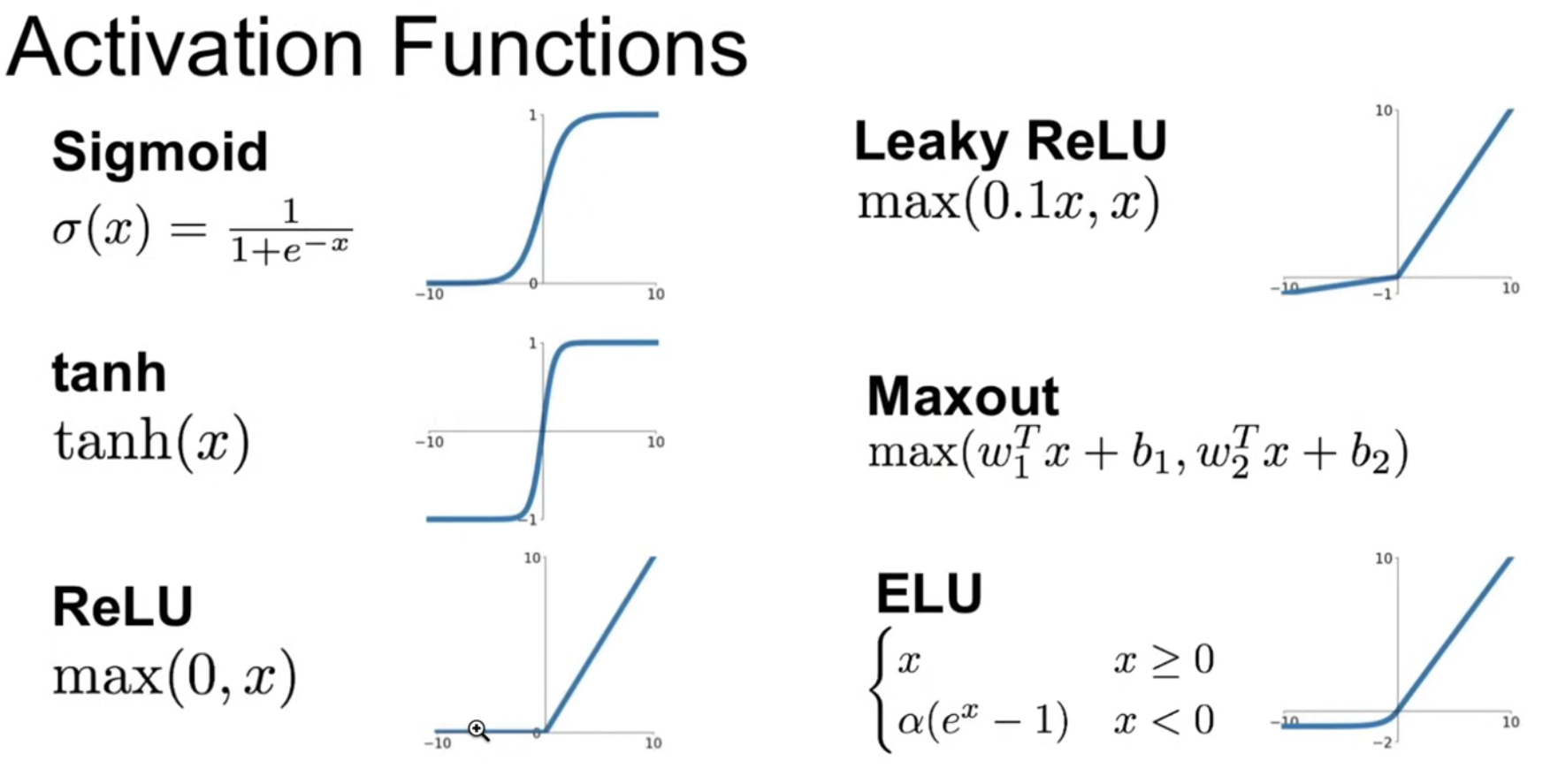
• it is a squashing function

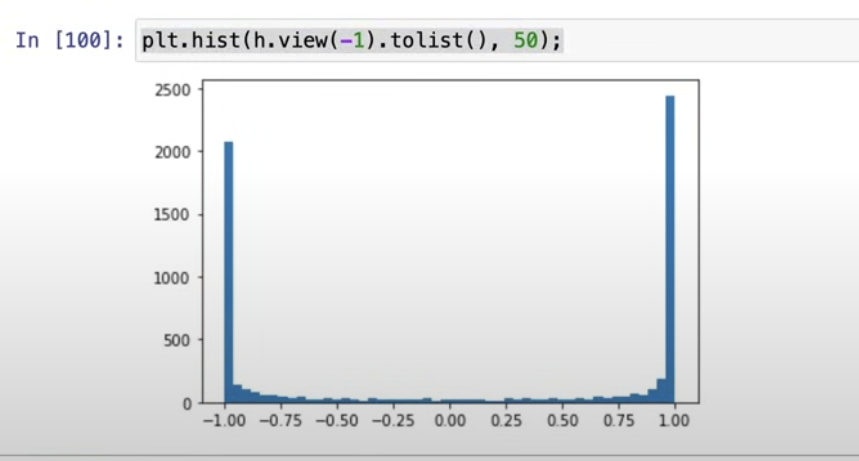
• if the value is 1 or -1 in backpropagation, the gradient is 0 so backpropagation stops: "dead neuron"

  • neuron output is all 1 or -1

• i.e. one column completely white

• same issue with sigmoid and relu

  • alternative: leaky relu or elu

• can happen at initialization or optimization (with high learning rate)

solution

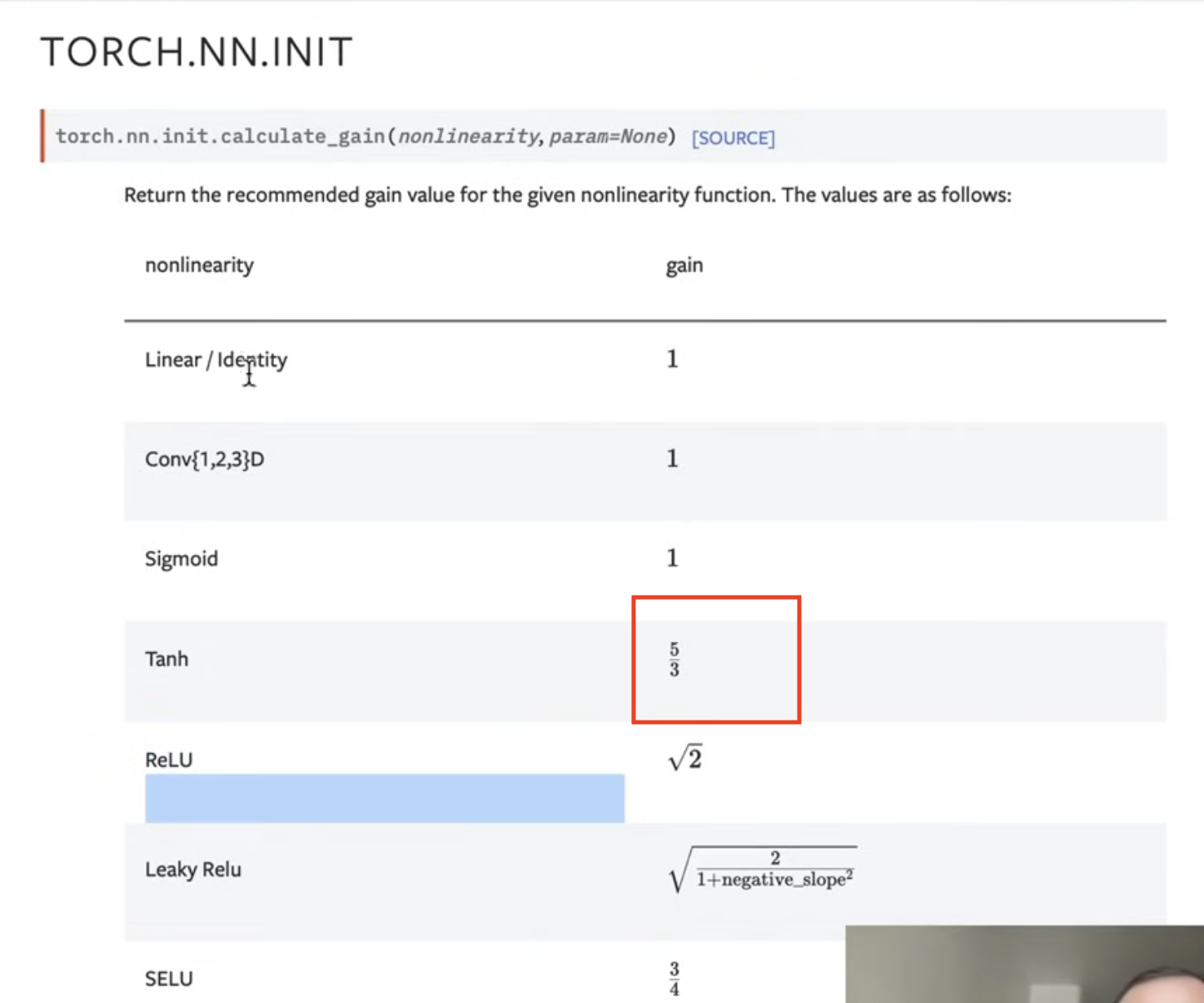
W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * (5/3)/((n_embd * block_size)**0.5)

• deeper the network the more significant the problem
• the multiplication above is trying to preserve the guassian distribution of the input (i.e. keeping a small standard deviation)
  • the factor is square root of (5/3)/ (n_embd * block_size)
  • Kaiming initialization

Batch normalization

• based on paper
• normalize the hidden layer

hpreact = embcat @ W1 #+ b1 # hidden layer pre-activation

1. Calculate the mean and standard deviation of the hidden layer

  bnmeani = hpreact.mean(0, keepdim=True)
  bnstdi = hpreact.std(0, keepdim=True)

• mean: taking mean of everything in the batch (average of any neuron activation)
• std: standard deviation of the batch
• remember we only want this at initialization, not during training

2. Scale and shift! (offset with gain and bias)

• note bngain and bnbias below

  hpreact = bngain * (hpreact - bnmeani) / bnstdi + bnbias
  with torch.no_grad():
    bnmean_running = 0.999 * bnmean_running + 0.001 * bnmeani
    bnstd_running = 0.999 * bnstd_running + 0.001 * bnstdi