添加主题模型文档。

Document/主题模型.md

@@ -0,0 +1,214 @@
+1. LDA是什么
+
+   隐含狄利克雷分布(Latent Dirichlet Allocation，以下简称LDA)，是由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出的一种主题模型，是一种无监督机器学习技术，它可以将文档集中每篇文档的主题以概率分布的形式给出，从而通过分析一些文档抽取出它们的主题（分布）出来后，便可以根据主题（分布）进行主题聚类或文本分类。同时，它是一种典型的词袋模型，即一篇文档是由一组词构成，词与词之间没有先后顺序的关系。
+
+   对于语料库中的每篇文档，LDA 定义了如下生成过程（generative process）：
+
+   1. 对每一篇文档，从主题分布中抽取一个主题； 
+   2. 从上述被抽到的主题所对应的单词分布中抽取一个单词； 
+   3. 重复上述过程直至遍历文档中的每一个单词。 
+
+   LDA 认为每篇文章是由多个主题混合而成的，而每个主题可以由多个词的概率表征。
+
+   LDA既给出了以上文档的具体生成过程，同时也给出了模型参数估计的方法。
+
+   LDA背后的数学原理相当复杂，这里只做大概的介绍，详细推导可看文末参考资料。
+
+2. LDA
+
+   LDA的相关内容可以做如下概括：
+
+   - 一个函数：gamma函数
+
+     gamma函数的表达式为：
+     $$
+     \Gamma(x)=\int_0^{+\infty}e^{-t}t^{x-1}dt \quad(x>0)
+     $$
+     gamma函数可以理解为阶乘的函数形式，因为：
+     $$
+     \Gamma(n)=(n-1)!
+     $$
+
+   - 四个分布：二项分布、多项分布、beta分布、狄利克雷分布
+
+     - 二项分布
+
+       二项分布即重复 n 次独立的伯努利试验。在每次试验中只有两 种可能的结果（成功/失败），每次成功的概率为 p，而且两种结果发生与否互相 对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变。
+
+       二项分布的概率密度函数为：
+       $$
+       f(k;n,p)=C_n^kp^k(1-p)^{n-k}
+       $$
+       其中n为总试验次数，p为成功概率，k为成功次数。
+
+     - 多项分布
+
+       多项分布是二项分布的推广，即每次实验的结果数大于两种，例如掷骰子就服从多项分布。
+
+       多项分布的概率密度函数为：
+       $$
+       f(x_1,...,x_k;n,p_1,...,p_k)=\left\{\begin{aligned}
+       \frac{n!}{x_1!...x_k!}p_1^{x_1}...p_k^{x_k}\quad\sum_{i=1}^kx_i=n
+       \\
+       0\qquad\qquad\qquad\qquad otherwise
+       \end{aligned}\right.
+       $$
+       其中n为总试验次数，k为每次实验的结果种数，$p_1,...,p_k$为每种结果出现的概率，$x_1,...,x_k$为每种结果出现的次数。
+
+       在对多项分布进行极大似然估计时，由于使用对数似然函数然后求导，多项分布概率密度前面的系数会被忽略掉，最后得到的估计值为：
+       $$
+       \widehat p_i=\frac{x_i}{n},i=1,...,k
+       $$
+       因此在多项分布的似然函数中常常忽略掉系数项。
+
+     - beta分布
+
+       beta 分布是指一组定义在区间(0,1)的连续概率分布，有两个 参数$\alpha>0,\beta>0$。
+
+       beta分布的概率密度函数为：
+       $$
+       f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1u^{\alpha-1}(1-u)^{\beta-1}du}
+       \\
+       =\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}
+       \\
+       =\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}
+       $$
+       beta分布的期望：
+       $$
+       E(p)=\frac{\alpha}{\alpha+\beta}
+       $$
+
+     - 狄利克雷分布
+
+       狄利克雷分布是beta分布在多项情况下的推广，其概率密度函数为：
+       $$
+       f(p_1,...,p_{k-1};\alpha_1,...,\alpha_k)=\frac{1}{\Delta(\vec\alpha)}\prod_{i=1}^kp_i^{\alpha_i-1}
+       \\
+       \sum_{i=1}^kp_i=1
+       \\
+       \Delta(\vec\alpha)=\frac{\prod_{i=1}^k\Gamma(\alpha_i)}{\Gamma(\sum_{i=1}^k\alpha_i)}=\int\prod_{i=1}^kp_i^{\alpha_i-1}d\vec p
+       $$
+       狄利克雷分布的期望：
+       $$
+       E(\vec p)=(\frac{\alpha_1}{\sum_{i=1}^k\alpha_i},...,\frac{\alpha_k}{\sum_{i=1}^k\alpha_i})
+       $$
+
+   - 一个概念：共轭先验
+
+     当后验分布函数与先验分布函数形式一致时，先验分布函数被称为似然函数的共轭先验分布。
+
+     - beta分布是二项分布的共轭先验分布：
+       $$
+       P(p|s,f,\alpha,\beta)=\frac{p^{s+\alpha-1}(1-p)^{f+\beta-1}}{B(s+\alpha,f+\beta)}
+       $$
+       其中，s、f分别为二项分布成功和失败的次数，后验分布也为beta分布，但超参数变了。如果以后有新增的观测值，后验分布又可作为先验分布来进行计算。具体来讲，在某一个时间点，有一个观测值，此时可以得到后验，之后，每一个观测值的到来，都以之前的后验作为先验，乘以似然函 数后，得到修正后的新后验。在这每一步中，其实我们不需要管什么似然函数， 我们可以将后验分布看作是以代表 x=1 出现“次数”的参数 s 和代表 x=0 出现 “次数”的参数 f 为参数的 beta 分布：当有一个新的 x=1 的观测量到来的时 候，s=$\alpha$+1,f=$\beta$，即$\alpha$的值相应的加 1;否则 s=$\alpha$ f=$\beta+1$，即$\beta$的值加 1。所以这也就是超参数$(\alpha,\beta)$又被称之为伪计数(pseudo count)的原因。
+
+     - 狄利克雷分布是多项分布的共轭先验分布：
+       $$
+       P(x_1,...,x_k;p_1,...,p_{k-1};\alpha_1,...,\alpha_k)=\frac{1}{\Delta(\vec\alpha+\vec x)}\prod_{i=1}^kp_i^{\alpha_i+x_i-1}
+       $$
+       类似于beta分布和二项分布，后验分布依然是超参数变化的狄利克雷分布，变化的参数为伪计数加上观测值中对应的出现”次数“。
+
+   - 四个模型：Unigram model、Mixture of unigrams model、pLSA、LDA
+
+     - Unigram model
+
+       对于文档$W=(w_1,w_2,...,w_N)$，用$p(w_n)$表示第n个词的先验概率，则生成文档W的概率为：
+       $$
+       p(W)=\prod_{i=1}^Np(w_n)
+       $$
+
+     - Mixture of unigrams model
+
+       该模型的生成过程是：给某个文档先选择一个主题z,再根据该主题生成文档，该文档中的所有词都来自一个主题。假设主题有 $\{z_1,z_2,...,z_K\}$，生成文档W的概率为：
+       $$
+       p(W)=p(z_1)\prod_{i=1}^Np(w_n|z_1)+...+p(z_k)\prod_{i=1}^Np(w_n|z_K)=\sum_{k=1}^Kp(z_k)\prod_{i=1}^Np(w_n|z)
+       $$
+
+     - pLSA
+
+       在上面的Mixture of unigrams model中，我们假定一篇文档只有一个主题生成，可实际中，一篇文章往往有多个主题，只是这多个主题各自在文档中出现的概率大小不一样。比如介绍一个国家的文档中，往往会分别从教育、经济、交通等多个主题进行介绍。
+
+       pLSA认为文档中的每一篇的生成过程为：
+
+       1. 以$p(d_i)$的概率选定文档$d_i$；
+       2. 以$p(z_k|d_i)$的概率选定主题$z_k$；
+       3. 以$p(w_n|z_k)$的概率选定词$w_n$。
+
+       文档中每个词的生成概率为：
+       $$
+       p(d_i,w_n)=p(d_i)p(w_n|d_i)=p(d_i)\sum_{k=1}^Kp(w_n|z_k)p(z_k|d_i)
+       $$
+       其中隐变量为$z_k$为隐变量，$\theta=((p(w_n|z_k),p(z_k|d_i)))$为参数，可以使用EM算法对其求极大似然概率或者是极大后验概率。
+
+     - LDA
+
+       在pLSA的思想上加上贝叶斯框架就能够得到LDA。LDA认为文档中的每一篇的生成过程为：
+
+       1. 按照先验概率$p(d_i)$选择一篇文档$d_i$；
+
+       2. 从狄利克雷分布$\alpha$中取样生成文档$d_i$的主题分布$\theta_i$；
+       3. 从主题的多项式分布$\theta_i$中取样生成文档$d_i$的第j个词的主题$z_{i,j}$；
+       4. 从狄利克雷分布$\beta$中取样生成主题$z_{i,j}$的词语分布$\phi_{z_{i,j}}$；
+       5. 从词语的多项式分布$\phi_{z_{i,j}}$中采样最终生成词语$w_{i,j}$。
+
+       可以用下图来表示LDA生成一篇文档的过程：
+
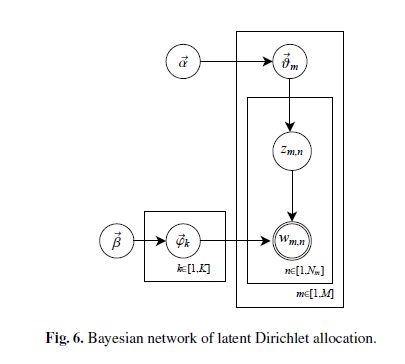+       [![ydFQu4.jpg](https://s3.ax1x.com/2021/02/09/ydFQu4.jpg)](https://imgchr.com/i/ydFQu4)
+
+       其中圆圈表示变量或参数；方框表示重复抽样，重复次数在方框的右下角；箭头表示两变量间的条件依赖性。
+
+   - 一个采样：Gibbs采样
+
+     Gibbs采样 是Markov-Chain Monte Carlo算法（MCMC）的一个特例。这个算法的运行方式是每次选取概率向量的一个维度，给定其他维度的变量值Sample当前维度的值。不断迭代，直到收敛输出待估计的参数。具体可以参考文末的Gibbs采样博客。
+
+3. 使用Collapsed Gibbs Sampling对LDA进行训练
+
+   训练集中所有词$\vec w$和主题的联合分布为：
+   $$
+   p(\vec w,\vec z|\vec \alpha,\vec \beta)=p(\vec w|\vec z,\vec \beta)p(\vec z|\vec \alpha)
+   \\
+   =\prod_{k=1}^K\frac{\Delta(\vec n_k+\vec \beta)}{\Delta(\vec \beta)}\prod_{m=1}^M\frac{\Delta(\vec n_m+\vec \alpha)}{\Delta(\vec \alpha)}
+   $$
+   其中，$\vec n_k$表示第k个主题的词分布向量，$\vec n_m$表示第m篇文档的主题分布。
+
+   Collapsed Gibbs Sampling的采样公式：
+   $$
+   p(z_i=k|\vec z_{\neg i},\vec w)=\frac{\Delta(\vec n_k+\vec \beta)}{\Delta(\vec n_{k,\neg i}+\vec \beta)}\frac{\Delta(\vec n_m+\vec \alpha)}{\Delta(\vec n_{m,\neg i}+\vec \alpha)}
+   \\
+   =\frac{n_{k,\neg i}^{(t)}+\beta}{\sum_{t=1}^Vn_{k,\neg i}^{(t)}+V\beta}\frac{n_{m,\neg i}^{(k)}+\alpha}{\sum_{k=1}^Kn_{m,\neg i}^{(k)}+K\alpha}
+   \\
+   =\hat \phi_{k,t}\hat \theta_{m,k}
+   $$
+   其中，$n_{k,\neg i}^{(t)}$表示主题k除去当前采样的单词后的词数，$n_{m,\neg i}^{(k)}$表示文档m除去当前采样的单词后的主题k的词数。上式引入了所谓的“对称超参数”，也即公式中每个$\alpha_i$和$\beta_i$都按同一个$\alpha$和$\beta$处理。
+
+   关于以上式子的推导可以参考文末链接的《LDA漫游指南》。
+
+4. 使用Gibbs采样对LDA进行推理
+
+   - 对当前文档中的每个单词w, 随机初始化一个主题编号z;
+   -  使用Gibbs采样公式，对每个词w重新采样其主题；
+   - 重复以上过程，直到Gibbs Sampling收敛；
+   - 统计文档中的主题分布。
+
+5. LDA的主题数目如何确定
+
+   - 基于经验，主观判断、不断调试、操作性强、最为常用。
+
+   - 基于困惑度，困惑度可以理解为对于一篇文章d，所训练出来的模型对文档d属于哪个主题有多不确定，这个不确定程度就是困惑度。困惑度的计算公式为：
+     $$
+     perplexity(D)=e^{-\frac{\sum \log p(w)}{\sum_{d=1}^MN_d}}
+     $$
+     其中D为测试集，指数的分子部分为测试集的总词数，分子为每个词的概率的对数。
+
+   - 使用Log-边际似然函数的方法，这个找了半天没找到详细解释，我的感觉就是上面的$\sum\log p(w)$即所有词生成的对数似然概率。
+   - 基于主题之间的相似度：计算主题向量之间的余弦距离，KL距离等，如果存在过于相似的主题，则降低主题数目。
+   - 非参数方法：Teh提出的基于狄利克雷过程的HDP法。
+
+**参考资料**：
+
+[LDA漫游指南](https://arxiv.org/ftp/arxiv/papers/1908/1908.03142.pdf)
+
+[ML-NLP/主题模型](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/5.3%20Topic%20Model#12-3%E4%B8%AA%E5%9F%BA%E7%A1%80%E6%A8%A1%E5%9E%8B%E7%9A%84%E7%90%86%E8%A7%A3)
+
+[Gibbs采样](https://www.cnblogs.com/pinard/p/6645766.html)

README.md

@@ -8,7 +8,7 @@
 
 Document文件夹下为笔记，Code文件夹下为代码，Data文件夹下为某些代码所使用的数据集，Image文件夹下为笔记部分所用到的图片。
 
-由于时间和精力有限，部分代码来自github开源项目，如Seq2Seq、Transformer等部分的代码。
+由于时间和精力有限，部分代码来自github开源项目，如Seq2Seq、Transformer等部分的代码，部分章节代码待补充。
 
 # 机器学习
 
@@ -28,8 +28,8 @@ Document文件夹下为笔记，Code文件夹下为代码，Data文件夹下为
 - 随机森林（[笔记](https://www.cnblogs.com/lyq2021/p/14253876.html)+[代码](Code/random_forest.py)）
 - XGBoost（[笔记](https://www.cnblogs.com/lyq2021/p/14253885.html)）
 - 聚类（[笔记](https://www.cnblogs.com/lyq2021/p/14341111.html)）
-- 特征工程之降维算法（[笔记](https://www.cnblogs.com/lyq2021/p/14364452.html)）
 - 特征工程之特征选择（[笔记](https://www.cnblogs.com/lyq2021/p/14367515.html)）
+- 特征工程之降维算法（[笔记](https://www.cnblogs.com/lyq2021/p/14364452.html)）
 
 # 深度学习
 
@@ -49,10 +49,5 @@ Document文件夹下为笔记，Code文件夹下为代码，Data文件夹下为
 - Transformer（[笔记](https://www.cnblogs.com/lyq2021/p/14330534.html)+[代码](https://github.com/1033020837/pytorch-seq2seq/blob/master/6%20-%20Attention%20is%20All%20You%20Need.ipynb)）
 - BERT（[笔记](https://www.cnblogs.com/lyq2021/p/14347124.html)）
 - LSTM+CRF进行序列标注（[笔记](https://www.cnblogs.com/lyq2021/p/14253897.html)）
-
-
-# 待添加部分
-
-- 主题模型
-- LightGBM
+- 主题模型（[笔记](https://www.cnblogs.com/lyq2021/p/14394558.html)）