Sorting Algorithms

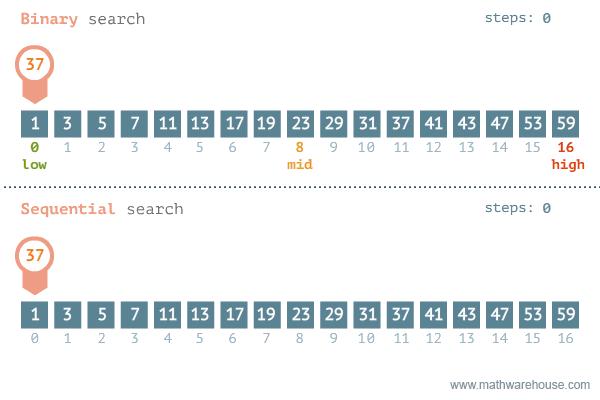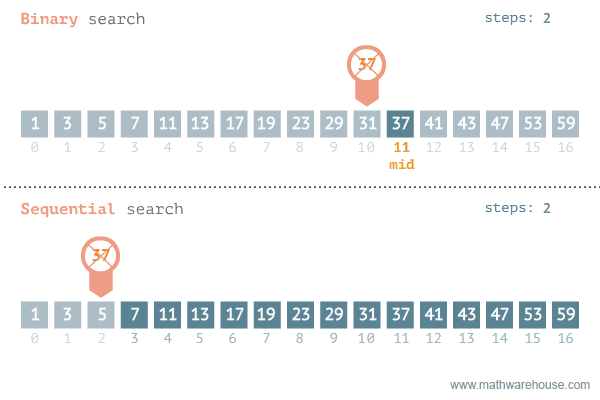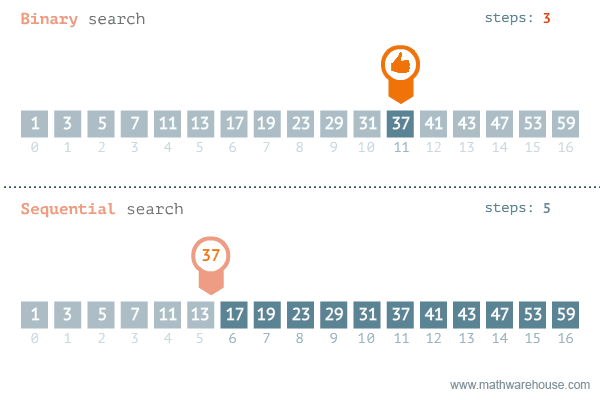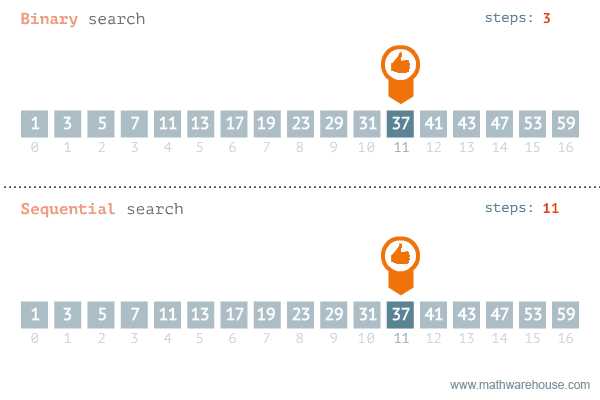
For the purpose of this module, we will be writing and discussing all sorting algorithms with the assumption that our goal is to sort items in ascending order. But be aware, this does not always have to be the case.

Part 1: Why is it So Important to Sort Data?

We're Always Searching

Users do not have patience for slow apps. And rightfully so! While a a big reason why the applications we use now-a-days are so fast is due to the improvements made in hardware over the last few decades, the software developer still has an important role to play in keeping everything moving quickly.

As we write our applications, we should always be mindful of what operations are being done frequently, since optimizing these will have the biggest impact on the efficiency of our overall application. And regardless of what type of app you are creating, it is likely that one of the operations you will be relying on is searching. We search for songs to add to a playlist, videos to watch, people we need to talk to and so much more. Because of this, it is essential that we optimize our searches.

Linear vs. Binary Search

There are two common searching algorithms that developers are often introduced to when they are writing some of their first apps: linear search and binary search. Let's walk through the differences between them.

Linear (Sequential) Search

Sometimes referred to as sequential search, this algorithm is fairly straightforward. Given a set of data, traverse the dataset one item at a time until either you find the item you are looking for OR check every item in the set and verify the item you are looking for is not there.

Binary Search

The process of performing a binary search has a couple of extra steps. First, there is a precondition that the set of data you are searching is already sorted (alphabetically, numerically, etc). Then, the steps to search are:

1. Compare the item in the middle of the data set to the item we are searching for.
   • If it is the same, stop. We found it and are done!
   • Else, if the item we are searching for is LESS than the item in the middle:
     • Eliminate the RHS of list. Repeat step 1 with only the LHS of list.
   • Else, the item we are searching for is GREATER than the item in the middle:
     • Eliminate the LHS of list. Repeat step 1 with only the RHS of the list.

A visualization comparing these two algorithms is shown below.

Your Task

• (STRETCH) Complete some or all of the three functions in searching.py

Runtimes

These two searching strategies have very different runtimes.

Linear Search: O(n)
Binary Search: O(log(n))

Looking at the above runtimes, it is clear that we should be using binary search over linear search. However, we cannot perform binary search if our data isn't ALREADY SORTED!

While the justification for WHY we want to sort our data is pretty clear, a harder question to answer is HOW do we want to sort our data. Over the next few days, we will explore several different sorting algorithms, examining the pros and cons of each.

Just for fun...(VIDEO) 15 Sorting Algorithms in 6 Minutes

Part 2: Iterative Sorting Algorithms

Insertion Sort

Think back to class or team picture day. Everyone stands in a line facing the photographer. Starting at the left-hand side of the line, the photographer checks to make sure each person is taller than the person next to them. If they are shorter, the photographer pulls them out and shifts people over to the right until he or she finds the right spot for this person. They then insert them back into the line. This process repeats until the photographer reaches the last person on the right-hand side, who must be the tallest person in the group. This is Insertion Sort.

(VIDEO) Insert-sort with Romanian folk dance

Algorithm

1. Separate the first element from the rest of the array. Think about it as a sorted list of one element.

2. For all other indices, beginning with [1]:

   a. Copy the item at that index into a temp variable

   b. Iterate to the left until you find the correct index in the "sorted" part of the array at which this element should be inserted

   • Shift items over to the right as you iterate

   c. When the correct index is found, copy temp into this position

Your Task

• Implement the insertion_sort() function in the Guided Project with your TA

Real-World Applications

The answer to the question, "Is Insertion Sort an efficient algorithm?" is not always the same. The runtime of Insertion Sort is dependent on how close to being "in-order" the data is to begin with. In a scenario where you are performing Insertion Sort on an already or mostly sorted array, very few elements will need to be shifted over, leading to a runtime of Ω(n). However, in a worse-case scenario, where the maximum number of shifts are being performed, the runtime of this algorithm is O(n²).

Selection Sort

Selection Sort is an algorithm that many of you have probably used before when sorting things in your everyday lives. Imagine that you have several books you want to arrange on a shelf from shortest to tallest. You start off by looking for the shortest book, and when you find it, put it on the far left side of the shelf. Then, you look for the second shortest book and insert it directly to the right of the first book. You repeat this process, selecting the next shortest book and moving it next to the most recently placed book, until you have moved all books into the correct place. This is Selection Sort.

An example of this algorithm being applied to an array with 10 numerical elements can be seen in the video below.

(VIDEO) Select-sort with Gypsy folk dance

Algorithm

1. Start with current index = 0

2. For all indices EXCEPT the last index:

   a. Loop through elements on right-hand-side of current index and find the smallest element

   b. Swap the element at current index with the smallest element found in above loop

Implementation in Python

def selectionSort(arr):
    # loop through n-1 elements
    for i in range(0, len(arr) - 1):
        cur_index = i
        smallest_index = cur_index
        # find next smallest element
        for j in range(cur_index, len(arr)):
            if arr[j] < arr[smallest_index]:
                smallest_index = j

        # swap
        temp = arr[smallest_index]
        arr[smallest_index] = arr[cur_index]
        arr[cur_index] = temp

    return arr

# try it out
my_arr = [2,5,9,7,4,1,3,8,6]
print(my_arr)
arr = selectionSort(my_arr)
print(my_arr)

Real-World Applications

While Selection Sort is one of the easier sorting algorithms to understand and implement, it has one major drawback - its efficiency.

Recall that the runtime complexity of an algorithm, often expressed using Big O notation, tells us how the amount of operations our algorithm requires will grow as the size of our input grows. Selection Sort has a runtime of O(n²), making it impractical to use with many large, real-world data sets.

Your Task

• Complete the missing parts of selection_sort() in iterative_sorting.py.

Bubble Sort

In Bubble Sort, we make a series of swaps between adjacent elements, gradually moving larger elements towards the end of the array (or bubbling larger elements up).

Algorithm

1. Loop through your array
   • Compare each element to its neighbor
   • If elements in wrong position (relative to each other, swap them)
2. If no swaps performed, stop. Else, go back to the element at index 0 and repeat step 1.

Real-World Applications

Bubble Sort is not ideal for many real-world applications. If a small element that should be at the beginning of our array is originally located near the end, it will take a long time to move it into its correct position.

However, it should be noted that if you perform Bubble Sort on an array that's already sorted, it will only require a single pass through the array, making its best-case performance linear.

Your Task

• Complete bubble_sort() in iterative_sorting.py.

TO-DO in iterative_sorting.py

• Complete selection_sort() and bubble_sort()

Stretch Goals

Try to write a search function

• Complete the functions in searching.py

There are a few "order n" sorting algorithms whose runtime will be linear, even in a worst case scenario.

Look into Counting Sort.

• How is this algorithm different from other iterative sorting algorithms?
  • What are the advantages/disadvantages to this type of sorting algorithm?
• Take a look a the pseudocode for this algorithm and try implementing it in Python.

You Might be Surprised at What Passes for a Sorting Algorithm

• Explore Bogo Sort and summarize how it works in a couple of sentences.

Part 3: A Better Way to Sort

Divide & Conquer

A divide-and-conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly.
-Wikipedia

This approach can be very useful when sorting. By breaking up our original data set into subsets and recursively sorting each subset, we can obtain significant performance gains.

Recursion Recap

Remember that when writing a recursive algorithm, there are two pieces we have to define:

• Base case
• Recursive case

Recursive cases must be written in a way that will eventually allow us to reach the base case. Otherwise, infinite recursion will lead to STACK OVERFLOW!

Recursive Sorting Algorithms

Quick Sort

Let's think about the group photo example again. Everyone's lined up and the photographer wants to order individuals from shortest to tallest. They pull out the first person from the line and instruct everyone shorter than this person to position themselves on the left-hand side. Everyone taller than this person is instructed to move to the right-hand side. The photographer then repeats this process with the group of people on the left and the group of people on the right. This is Quick Sort.

(VIDEO) Quick-sort with Hungarian folk dance

Algorithm

1. Select a pivot. Often times this is the first or last element in a set. It can also be the middle.
2. Move all elements smaller than the pivot to the left. 
3. Move all elements greater than the pivot to the right.
4. While LHS and RHS are greater than 1, repeat steps 1-3 on each side.

Your Task

• Implement the quick_sort() function in the Guided Project with your TA

Real-World Applications

While Quick Sort has "quick" in its name, it is typically not used as frequently as Merge Sort. Although it is quick in a best case scenario, worst case for Quick Sort is very bad. Because of this, it is not often chosen for production.

Merge Sort

Your boss asks you to organize an old filing cabinet with 20 years worth of financial documents. He would like things ordered chronologically. You feel overwhelemed. There are thousands of papers in this thing. So you decide to break this insane task up into more manageable pieces. First, you focus on organizing a single drawer. But this still has a lot of pieces of data that need to be sorted. Within the drawer, you pull out a single folder. You lay out all the contents on a table, grabbing two pieces at a time, placing the older document on top of the newer one. Then, you start merging sorted sets of documents together until the folder is done. Once all the folders have been reassembled, you order the folders correctly in the drawer. And then you put sorted drawers back into the filing cabinet. This idea of breaking a large set of data down into small pieces, sorting the pieces, then merging them back together is what Merge Sort is all about.

(VIDEO) Merge-sort with Transylvanian-saxon (German) folk dance

Algorithm

1. While your data set contains more than one item, split it in half
2. Once you have gotten down to a single element, you have also *sorted* that element 
   (a single element cannot be "out of order")
3. Start merging your single lists of one element together into larger, sorted sets
4. Repeat step 3 until the entire data set has been reassembled

Real-World Applications

Have you ever wondered how some of the languages you use actually implement their built-in sort() functions? Many of them actually utilize the Merge Sort algorithm! WHY they do so is because this sorting algorithm is reliably efficient. In all cases, regardless of how sorted the original data set might be, this algorithm will have a runtime of O(n log(n)), one of the better sorting runtimes out there.

Your Task

• Implement merge_sort() in recursive_sorting.py. It's recommended that you use...
  • A recursive function that handles dividing the array (or subarray) in half
  • A helper function that handles merging sorted pieces back together
• STRETCH - Try writing an in-place Merge Sort algorithm.

TO-DO in recursive_sorting.py

• Implement the merge_sort()

Stretch Goals

Make a better Merge Sort

• While a little more challenging, it is possible to implement Merge Sort in-place (without using extra memory). Try writing a second merge_sort() function that does this.

Timsort is a combination of the Merge Sort and Insertion Sort algorithms.

• What programming languages use Timsort to implement their built-in sort() functions?
• If an interviewer asked you to describe the Tim Sort algorithm in 3-4 sentences, what would you say?
• Can you implement Tim Sort in Python?