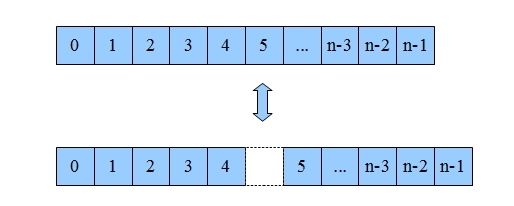
数组是一种顺序存储结构，当数组被声明时它会划分出一块连续的地址。正因为它是连续的，利用元素的索引（index）可以计算出该元素对应的存储地址。
优点：
- 无论数组有多大，根据索引位置只需要一次操作就可货取元素的内容，查询效率高。数组的查询操作的时间复杂度为O(1)。
缺点：
- 同样因为数组的内存地址是连续的，插入（删除）一个元素时，该元素的所有后继元素都要挪动位置，所以插入和删除操作效率低下。数组的插入和删除操作时间复杂度为O(n)。
- 大小固定，不支持扩展。
注意：当有序线性表查找的时间复杂度为O(1) 时，折中查找的时间复杂度为O(logN)。
链表是一种链式存储结构，它是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)，将一些不连续的内存空间串连起来。
优点：
- 链表在插入和删除操作时只需要改变某一结点的指针域，所以插入和删除操作效率高，时间复杂度为O(1)。
- 大小不固定，支持扩展。
缺点：
- 索引访问慢，时间复杂度为O(n)
链表中最简单的一种是单向链表，它包含两个域，一个信息域和一个指针域。这个链接指向列表中的下一个节点，而最后一个节点则指向一个空值。
在单向链表的基础上，每个节点有两个两个指针，一个指向前驱节点，另一个指向后驱节点。
普通链表的尾节点后继指针指向None，而循环链表的尾节点后继指针指向头节点
-
寻找链表中的倒数第n个结点。
解决思路：建立p_node和p_temp两个指针，并令他们都指向头链表头部。等p_temp移动了n次以后，再开始移动p_node。接下来，同时移动这两个指针，直到p_tmep越过链表末尾为止。此时p_node所指向的结点正是链表的倒数第n个结点。
算法复杂度：时间复杂度O(n)，空间复杂度O(1)。 -
判断链表中是否包含环？找出环的入口结点。
解决思路：问题1——弗洛伊德循环查找算法。用两个速度不相同的指针来遍历链表。只要二者相遇，就说明链表中有循环。问题2——在解决问题1的基础上，令其中一个指针指向链表的头结点，并且令两个指针都继续移动，只不过每次只走一个结点而已。两者再度相遇之处，就是循环的入口结点。（图伦方面的知识）
算法复杂度：时间复杂度O(n)，空间复杂度O(1)。 -
反转单链表。
算法复杂度：时间复杂度O(n)，空间复杂度O(1)。
堆栈（stack）又称为栈或堆叠，是一种抽象数据类型，只允许在有序的线性数据集合的一端（堆栈顶端, top）进行加入数据（push）和移除数据（pop）的运算。因而按照后进先出（LIFO, Last In First Out）的原理运作。
队列，是先进先出（FIFO, First-In-First-Out）的线性表。在具体应用中通常用链表或者数组来实现。队列只允许在后端（rear）进行插入操作，在前端（front）进行删除操作。
优先队列不再遵循先入先出的原则,从”优先“一词，可看出有“插队现象”。优先队列至少含有两种操作的数据结构：insert（插入），即将元素插入到优先队列中（入队）；以及deleteMin（删除最小者），它的作用是找出、删除优先队列中的最小的元素（出队）。
优先队列的实现常选用二叉堆，在数据结构中，优先队列一般也是指堆。
堆的两个性质：
- 结构性：堆是一个完全二叉树。
- 堆序性：由于我们想很快找出最小元，则最小元应该在根上，任意节点都小于它的后裔，这就是小顶堆（Min-Heap）；如果是查找最大元，则最大元应该在根上，任意节点都要大于它的后裔，这就是大顶堆(Max-heap)。
哈希表（也叫散列表），是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，这加快了查找速度。这个映射函数称做哈希函数，存放记录的数组称做哈希表。
基本概念：
- 若关键字为 k，则其值的存放位置为F(k)。称这个对应关系F为哈希函数，按这个思想建立的表为哈希表。由此，查询只需通过一次运算，而无需遍历哈希表确定位置。查询的时间复杂度为O(1)。
- 对不同的关键字可能得到同一哈希地址，即k1 ≠ k2，而f(k1) = f(k2)，这种现象称为冲突。
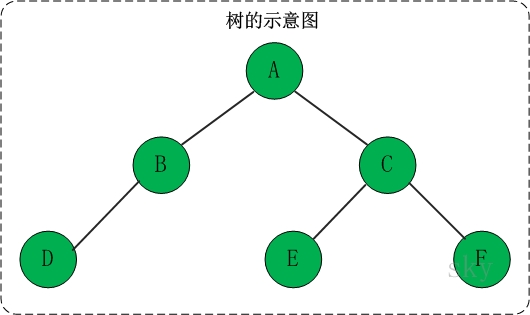
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的特性：
- 性质1：二叉树第i层上的结点数目最多为 2^(i-1) (i≥1)。
- 性质2：深度为k的二叉树至多有2^k-1个结点(k≥1)。
- 性质3：包含n个结点的二叉树的高度至少为log2 (n+1)。
- 性质4：在任意一棵二叉树中，若终端结点的个数为n0，度为2的结点数为n2，则n0=n2+1。
高度为h，并且由2^h–1个结点的二叉树，被称为满二叉树。
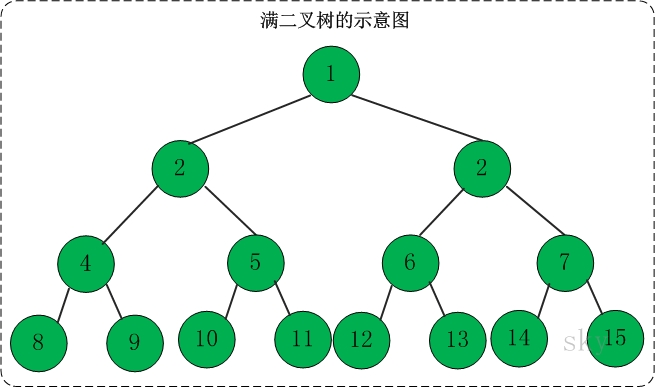
一棵二叉树中，只有最下面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。
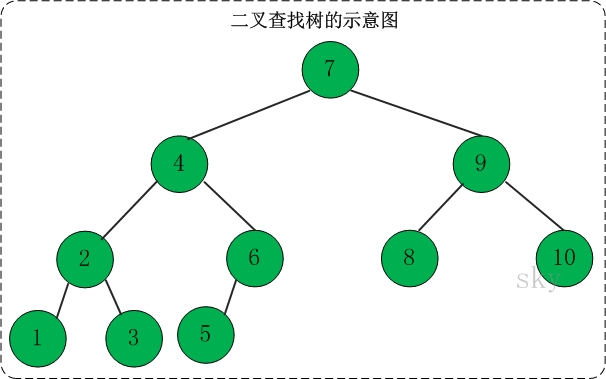
二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。
二叉搜索树的特性:
- 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
- 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点（no duplicate nodes）。