Ant Colony Optimisation

The idea of this algorithm comes from the ant behavior when they transport food from the source to their anthill. They find the shortest path between the two points by leaving pheromone along their path. At the beginning the ants are exploring multiple paths to get to their destination, but since the pheromone evaporates, a path with a lot of pheromone indicates that an ant where there a short time ago, thus that this path is probably shorter than the other.

This method can be applied to find a good solution for the Travelling Salesman Problem for example, known as a NP-hard problem. As emphasized, it does not solve the problem by finding the best solution, (which can be obtained using the Held-Karp algorithm) but provides an acceptable solution in an acceptable time (the user fixes the number of iteration) for a large dimensions problem.

Here is a short description of the algorithm (multiple versions exist):

1. The graph is initialized by leaving the same value of pheromone on every arcs (every node of the problem is linked to all the remaining nodes), and the ants are randomly assigned to one of the node.
2. At each iteration, every ant finds a solution to the problem, by going through every nodes and comes back to its initial node.
3. To select in which city the ant should go, a probability is assigned to each arc, representing its attractiveness (combination of its pheromone value and its distance). The arc is then selected by drawing a sample from this probability law.
4. At the end of the iteration, the pheromone on every arc is updated:
   • some pheromone is removed since it evaporates
   • some pheromone is added, depending on the total distance travelled by every ant: the smaller the distance, the larger the added pheromone on its path.
5. The stopping criterion is the number of iteration (can be the fact that the best solution is not evolving during n iterations.)

The important parameters are:

• the value of pheromone which evaporates at each iteration
• a parameter alpha controlling the importance of the pheromones during the selection of the next node
• a parameter beta controlling the importance of the distance of the arc during this same selection

Example: solving the TSP across European cities

I'm using Streamlit to build a nice visualisation, in which you can easily teak the parameters and check their impact on the solution.

The requirements (only streamlit for now) can be installed with

pip install -r requirements.txt

Then, the app can be accessed by running

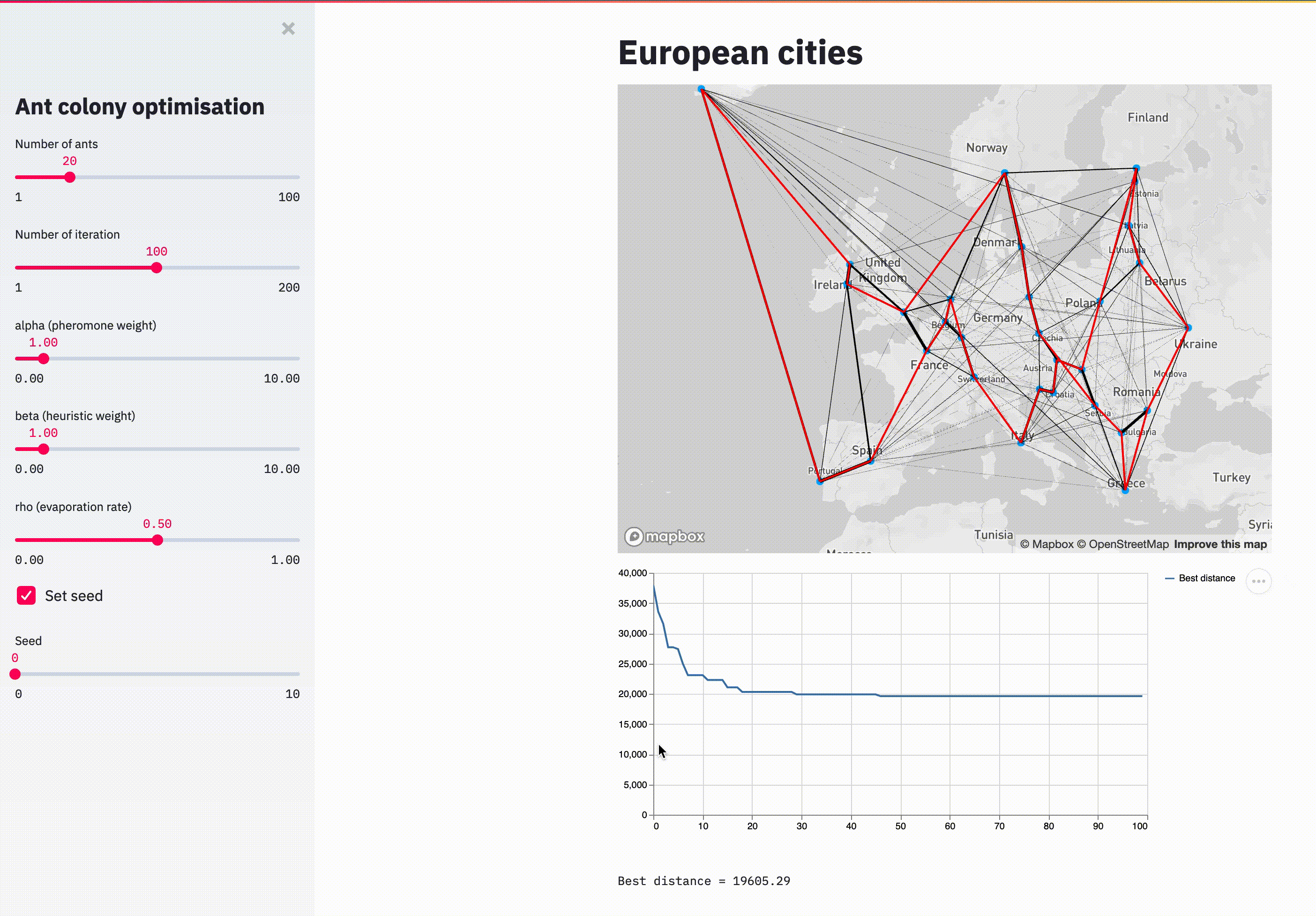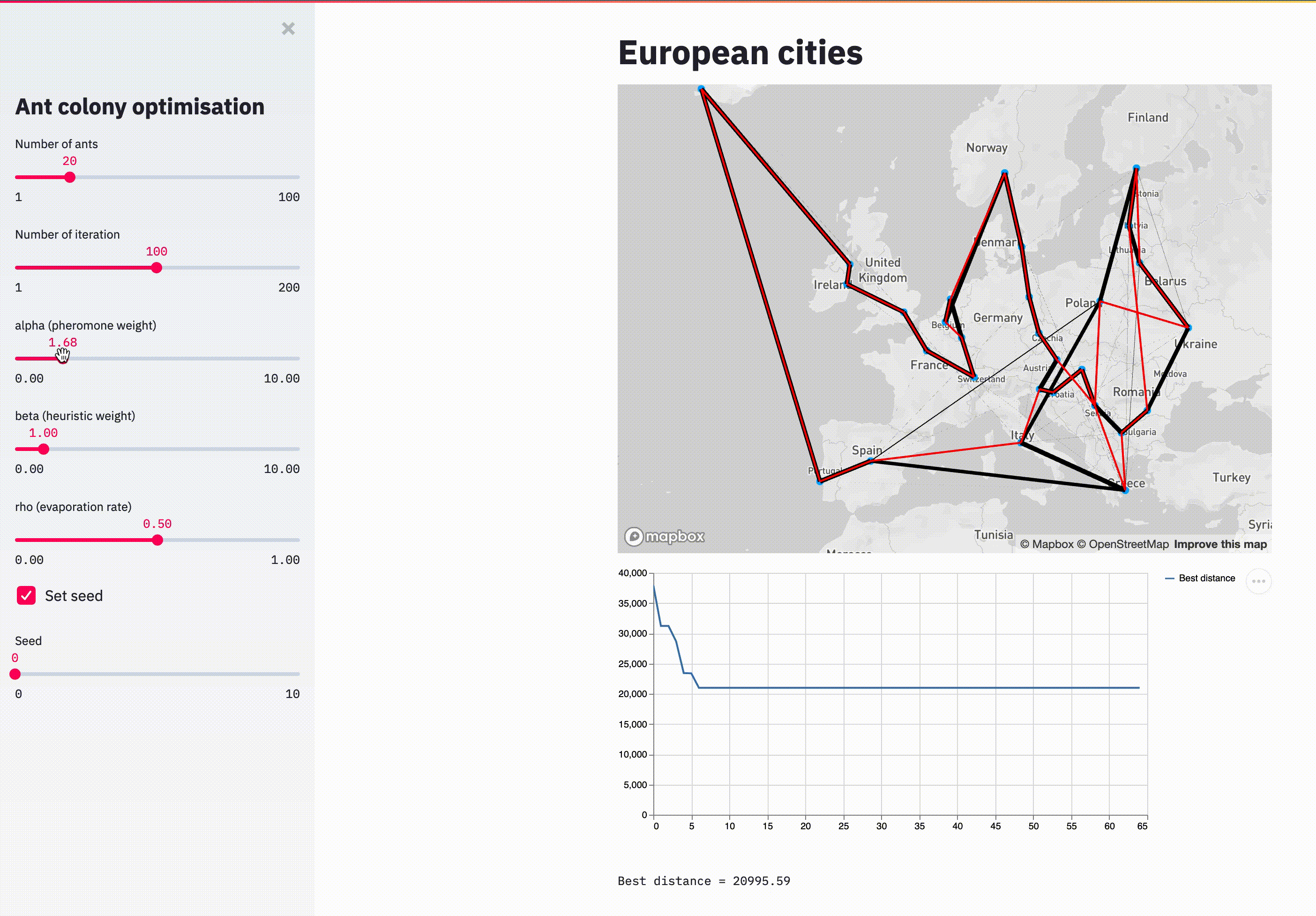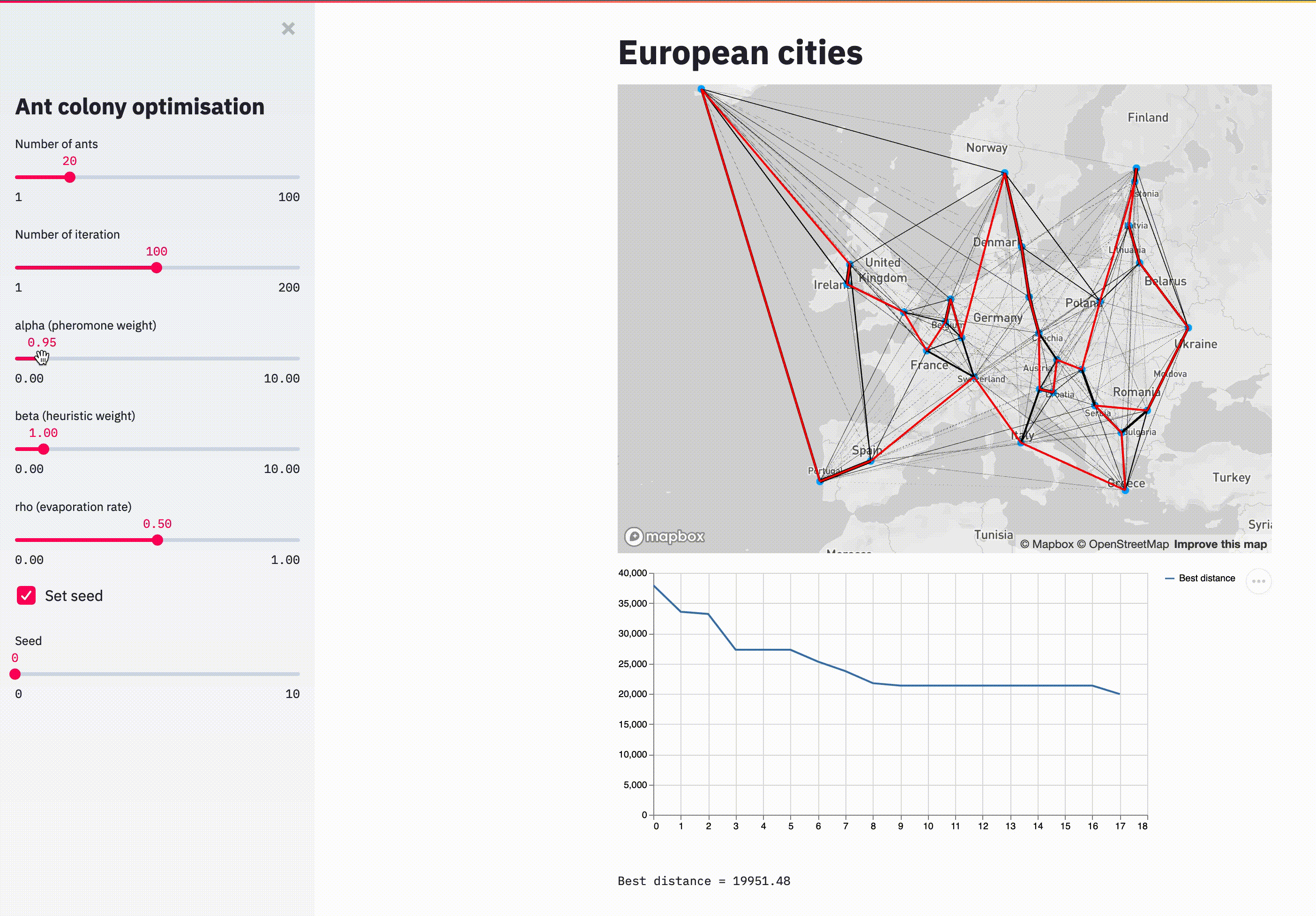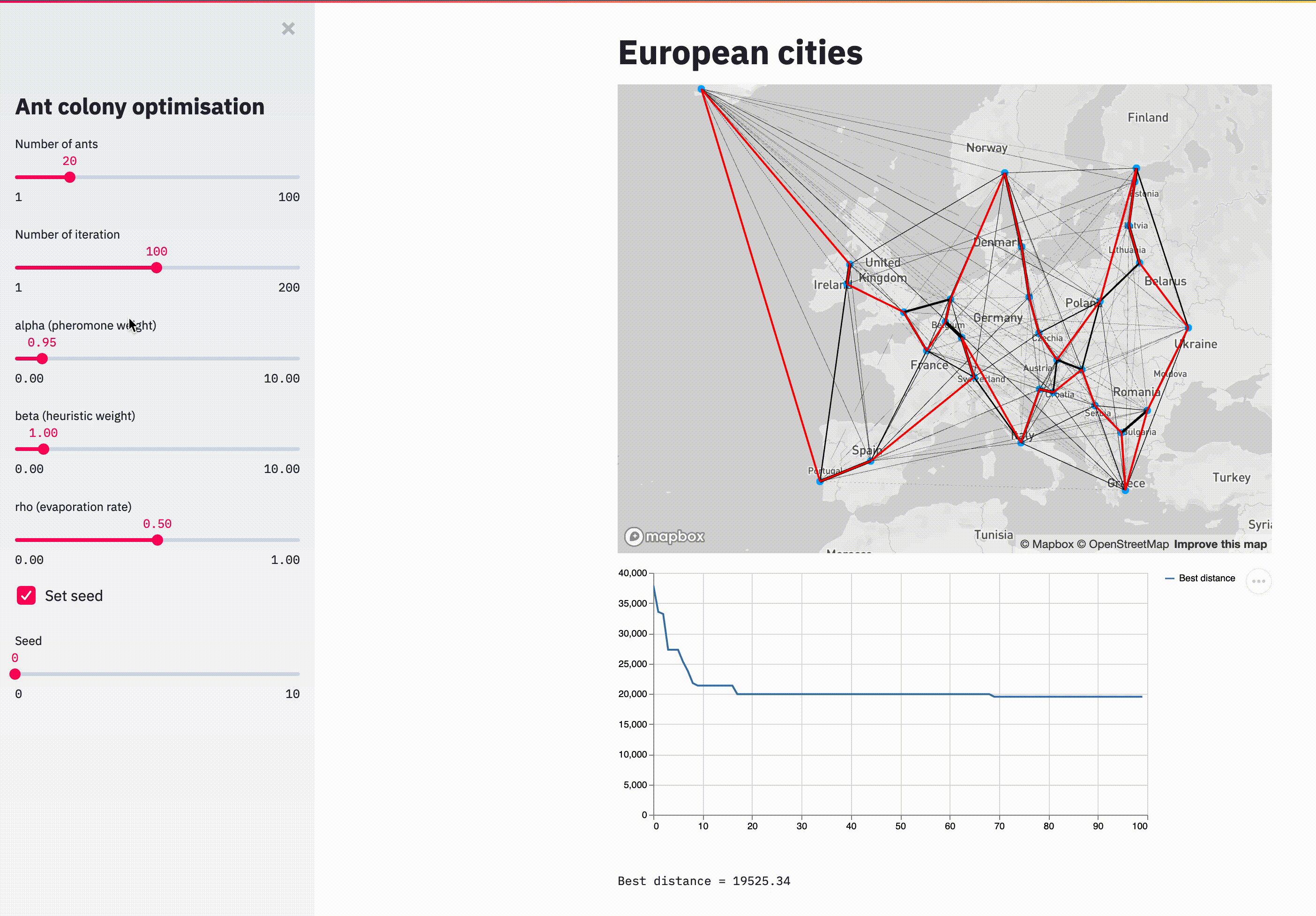
streamlit run main.py

Here is an animation showing the evolution of the pheromone on each arc (black lines), the current best path (in red) and the distance convergence.

With 100 iterations, the solution doesn't look optimal but it's reasonable.