🦔 PANGOLINPATHFINDER

❓ 问题描述

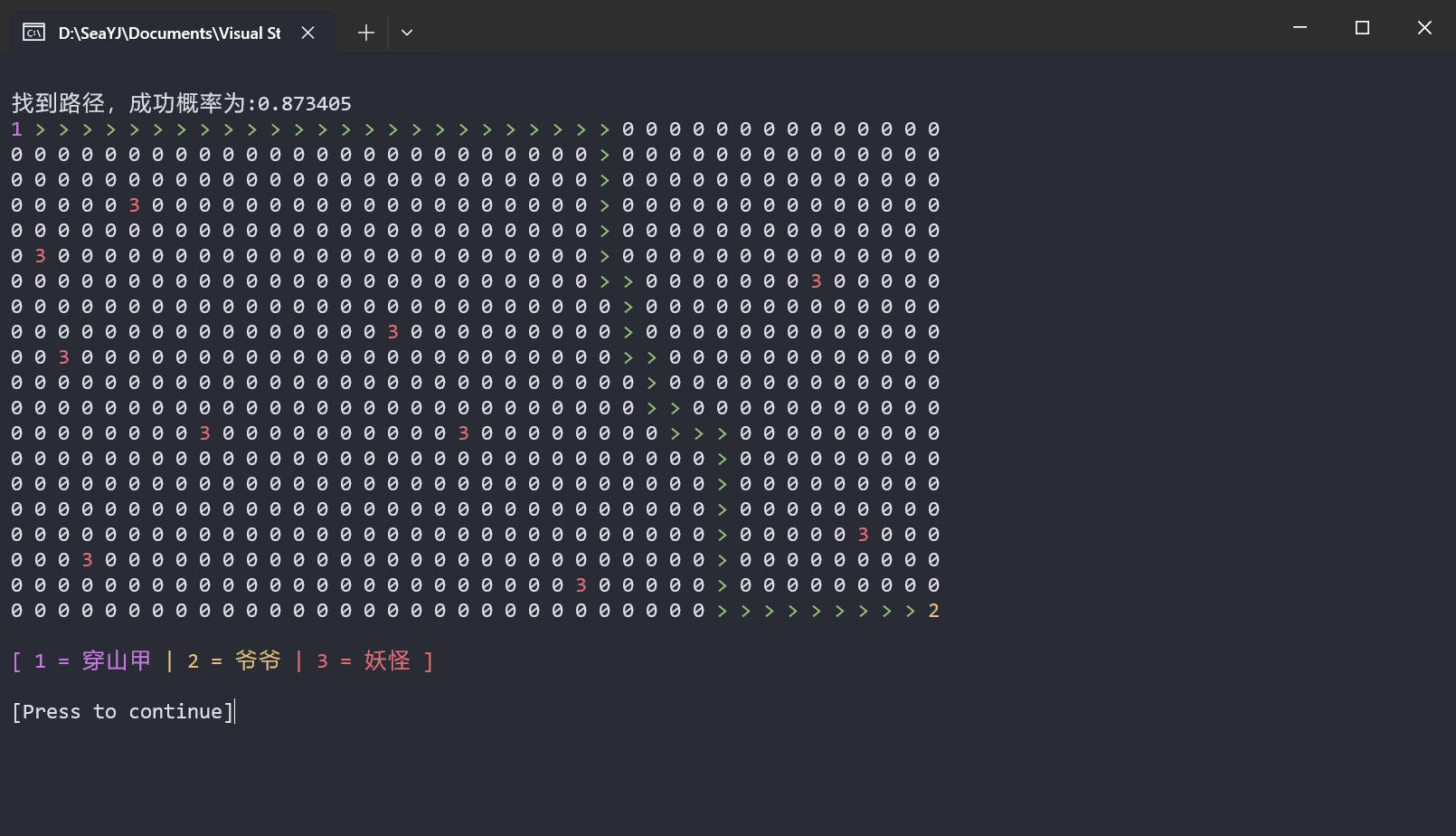
拯救爷爷：穿山甲想要在山里中挖出一条路径，来解救被妖怪囚禁的爷爷。假如穿山甲挖的路径都是在平面内。妖怪数量和位置、爷爷被囚禁的位置都由用户输入。假如穿山甲挖洞的动静惊动妖怪的概率，与其所处的位置与最近的妖怪距离成反比，现在为穿山甲指出一条成功概率最高的路径，并输出此路径的成功概率值。

💻 基础算法

基于 Dijkstra 算法实现了一个带权重的最短路径搜索算法，使用优先队列进行搜索，并且在计算路径权重时考虑了路径上每一步的惊动概率。从而找到一个最短的、成功率最高的路径。

👁‍🗨 惊动概率的数学模型

1. 每步的惊动概率 Pi：仍然使用 Pi = k / d 的公式，其中 d 是当前节点与最近妖怪的距离，k 是一个常数，用于调整惊动概率的量级，可证 0 < Pi <= 1/(√2)。
2. 整条路径的累积惊动概率 P：采用线性累加的方式计算路径总惊动概率：P_total = Σ Pi。为了确保 P_total 在梯度变化合理范围内，引入一个归一化系数 alpha，使得 P = 1 - exp(-alpha * P_total)，其中 alpha 可以根据路径长度进行调整。路径成功概率：
3. 成功概率 SuccessProbability：最后 SuccessProbability = P。

🕒 程序运行截图

➕ 补充

证明 0 < Pi <= 1 / √2

已知： Pi = 1 / (√((Xi - monster.Xi)^2 + (Yi - monster.Yi)^2))

设 Ai = √((Xi - monster.Xi)^2 + (Yi - monster.Yi)^2)、 Bi = Xi - monster.Xi、 Ci = Yi - monster.Yi。

则 Pi = 1 / Ai = 1 / (√(Bi^2 + Ci^2))

因为 Xi != monster.Xi && Yi != monster.Yi， 所以 Bi != 0 && Ci != 0， 所以 Ai != 0，即 Pi != 0。 又因为 Ai > 0，可得 Pi > 0。

因为 Xi、monster.Xi、Yi、monster.Yi ∈ N 且 Xi != monster.Xi && Yi != monster.Yi， 所以 Bi、Ci ∈ N+， 所以 MIN(Bi) = 1、MIN(Ci) = 1， 所以 MIN(Bi^2 + Ci^2) = 2， 所以 MAX(Pi) = MAX(1 / Ai) = 1 / √2， 所以 Pi <= 1 / √2。

综上，0 < Pi <= 1 / √2。