Homework 8 在我的虚拟机(ubuntu 22.04)上编译运行时出现段错误,原因不明,但在另一虚拟机(ubuntu 20.04)上则可以正常编译运行
$$
\begin{pmatrix}
a&b&c&t_x\\
d&e&f&t_y\\
g&h&i&t_z\\
0&0&0&1\\
\end{pmatrix}=
\begin{pmatrix}
1&0&0&t_x\\
0&1&0&t_y\\
0&0&1&t_z\\
0&0&0&1\\
\end{pmatrix}\begin{pmatrix}
a&b&c&0\\
d&e&f&0\\
g&h&i&0\\
0&0&0&1\\
\end{pmatrix}
$$
$$
变换=平移变换\times线性变换
$$
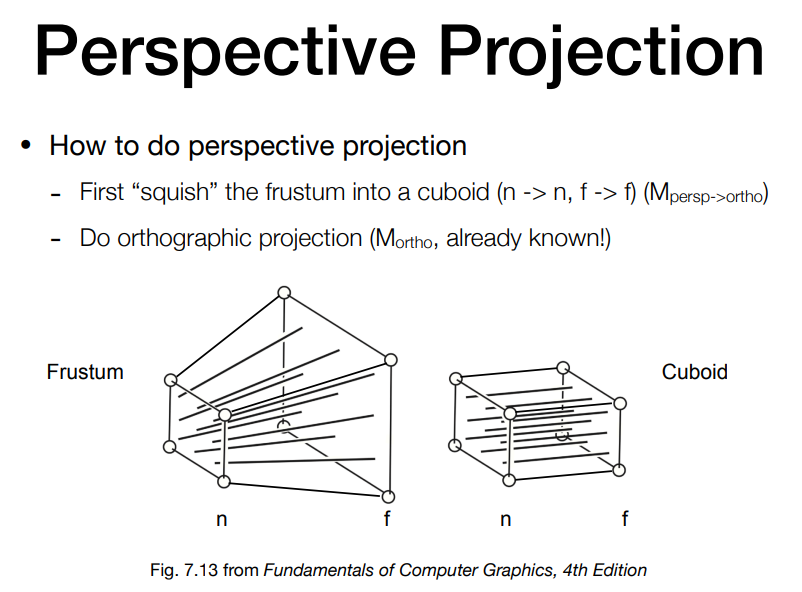
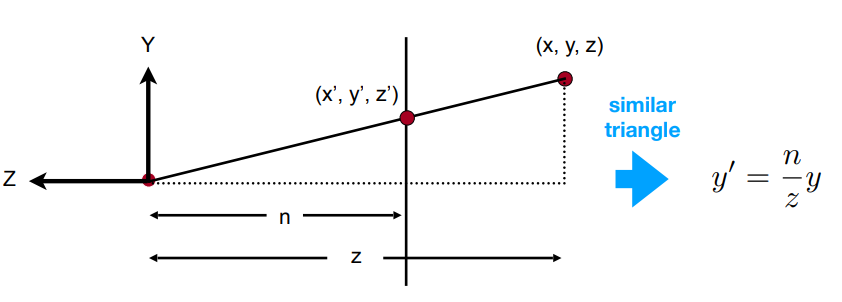
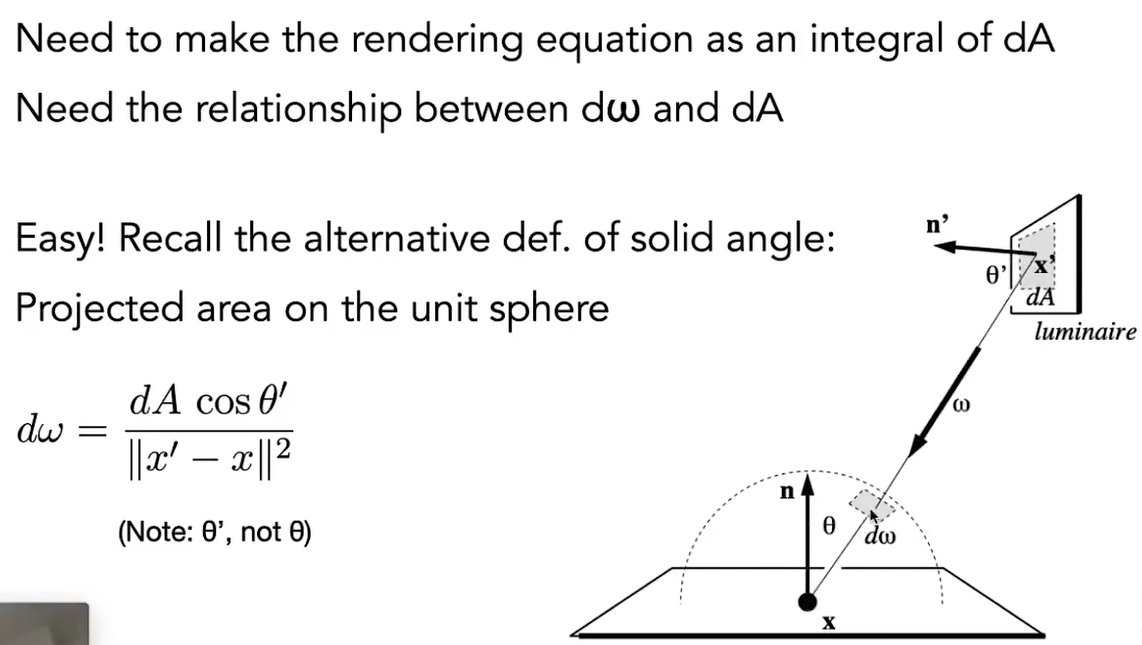
对远端平面上的任意一点,x、y 坐标的缩放如下图所示
n 为原点与近端平面的距离
因此变换后的齐次坐标为
$$
\begin{pmatrix}
nx/z\ny/z\z'\1
\end{pmatrix}==\begin{pmatrix}
nx\ny\zz'\z
\end{pmatrix}
$$
设变换矩阵的为
$$
\begin{pmatrix}
n&0&0&0\\
0&n&0&0\\
A&B&C&D\\
0&0&1&0\\
\end{pmatrix}
$$
近端平面上任意一点的坐标不变(规定)为 n
$$
\begin{pmatrix}
x\y\n\1
\end{pmatrix}==\begin{pmatrix}
nx\ny\n^2\n
\end{pmatrix}
$$
因此
$$
\begin{pmatrix}
A&B&C&D
\end{pmatrix}\begin{pmatrix}
x\y\n\1
\end{pmatrix}=Ax+By+Cn+D=n^2\\
=>A=B=0
$$
远端平面上任意一点的 z 坐标不变(规定)为 f
$$
\begin{pmatrix}
0&0&C&D
\end{pmatrix}\begin{pmatrix}
x\y\f\1
\end{pmatrix}=Cf+D=f^2
$$
联立解得
$$
C=n+f\\
D=-nf
$$
因此透视投影的变换矩阵为
$$
\begin{pmatrix}
n&0&0&0\\
0&n&0&0\\
0&0&n+f&-nf\\
0&0&1&0\\
\end{pmatrix}
$$
对梯形中的任意一点,变换之后的坐标为
$$
\begin{pmatrix}
n&0&0&0\\
0&n&0&0\\
0&0&n+f&-nf\\
0&0&1&0\\
\end{pmatrix}\begin{pmatrix}
x\y\z\1
\end{pmatrix}=\begin{pmatrix}
nx\ny\(n+f)z-nf\z
\end{pmatrix}\\
其中\ f\le z\le n\lt0
$$
计算可知
$$
\frac{(n+f)z-nf}{z}\le z
$$
因此变换之后,梯形体内部的 z 坐标相比变换前变小了,也即变远了
傅里叶变换的性质
$$
F[f_1(t)]=F_1(x)\\
F[f_2(t)]=F_2(x)\\
F[f_1*f_2]=F_1\times F_2
$$
三维空间中三角形内点的重心坐标,在投影到二维平面上后发生改变 因此对像素做插值时,应该先将像素中心坐标变换回原三角形中的坐标,再求其重心坐标并插值
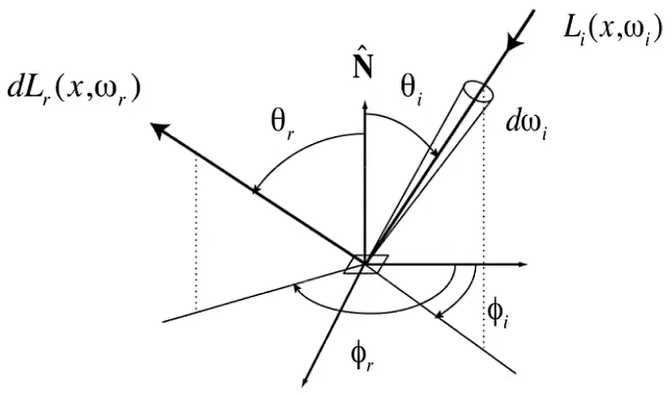
对任意入射光线,在任意反射方向下的反射能量的分布,定义材质的反射性质
$$
f_r(\omega_i\rightarrow\omega_r)=\frac{dL_r(\omega_r)}{dE_i(\omega_i)}=\frac{dL_r(\omega_r)}{L_i(\omega_i)\cos{\theta_i}d\omega_i}
$$
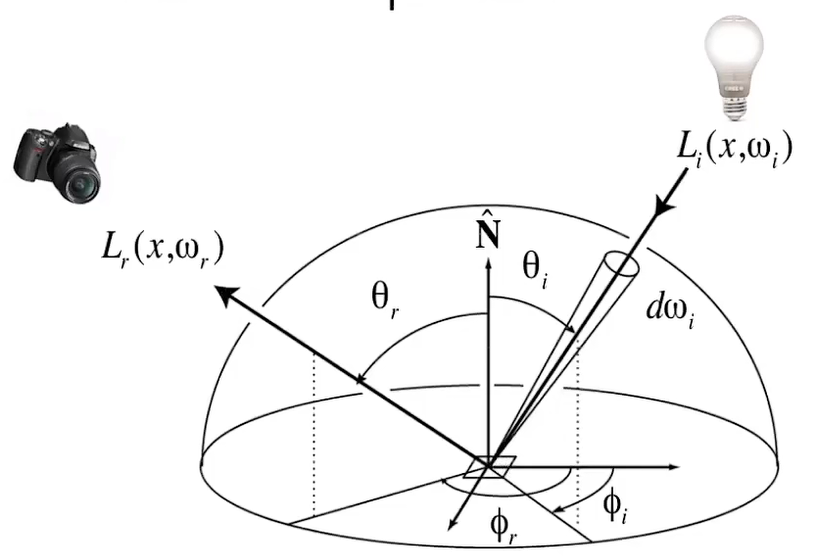
对所有入射方向做积分(也即对所有入射光线求和)
$$
L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i\rightarrow\omega_r)L_i(p,\omega_i)\cos{\theta_i}d\omega_i\\
=\int_{H^2}f_r(p,\omega_i\rightarrow\omega_r)E_i(p,\omega_i)
$$
递归则描述光线多次反射的过程
在反射方程中加入自发光项
$$
L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)d\omega_i
$$
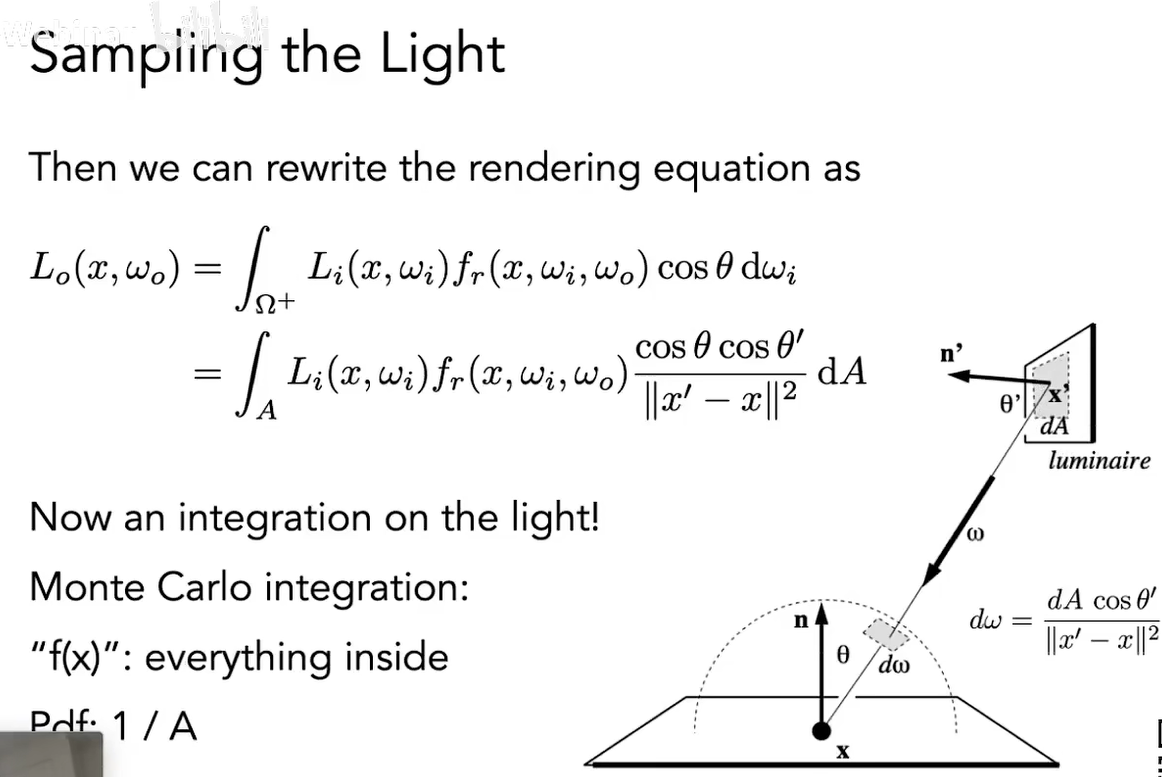
由于光线可以在物体表面间弹射,为了求解全局光照,将渲染方程记作如图形式
对入射光线求反射的过程可以简写为一个算符
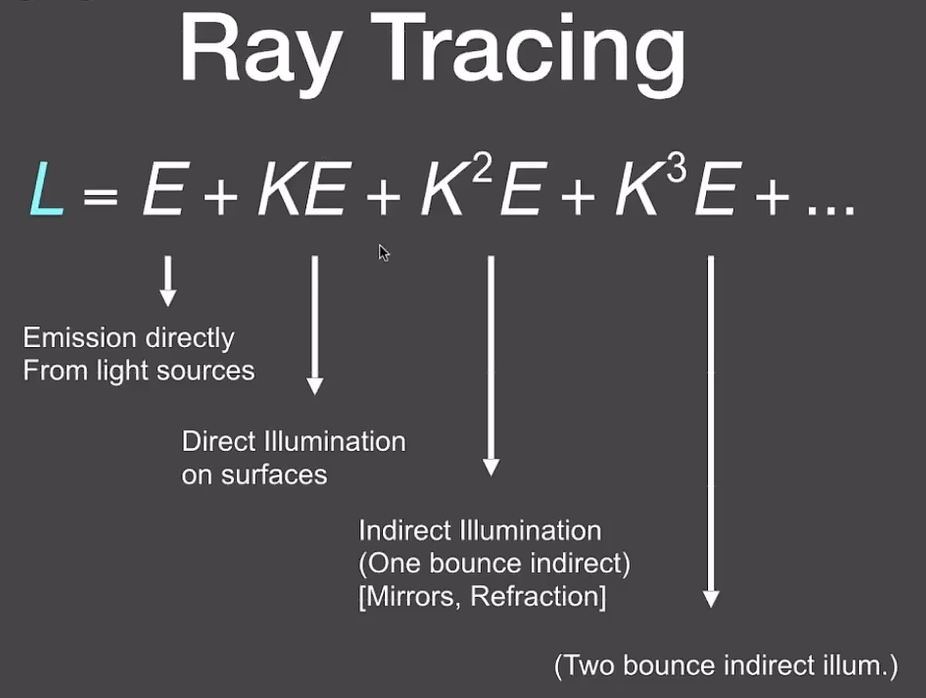
即得全局光照方程,其中各项的物理意义即为:光源项、表面反射项、弹射一次的表面反射项、弹射两次的表面反射项等
其中除前两项(直接光照)外,(间接光照)更适合用光线追踪方法完成
以积分的积分域为定义域取一随机变量$X$,求出其概率密度函数,进行多次采样,然后求平均值
特殊情况:均匀采样
从 Whitted-Style 光线追踪到路径追踪 首先,渲染方程没有错误,但其中有两个问题
$$
L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(n\cdot\omega_i)d\omega_i
$$
包含积分项
包含递归定义
解决的方法:
蒙特卡洛积分
图中蓝色 Else 项即为间接光照项。若遇到其他物体,则进行递归
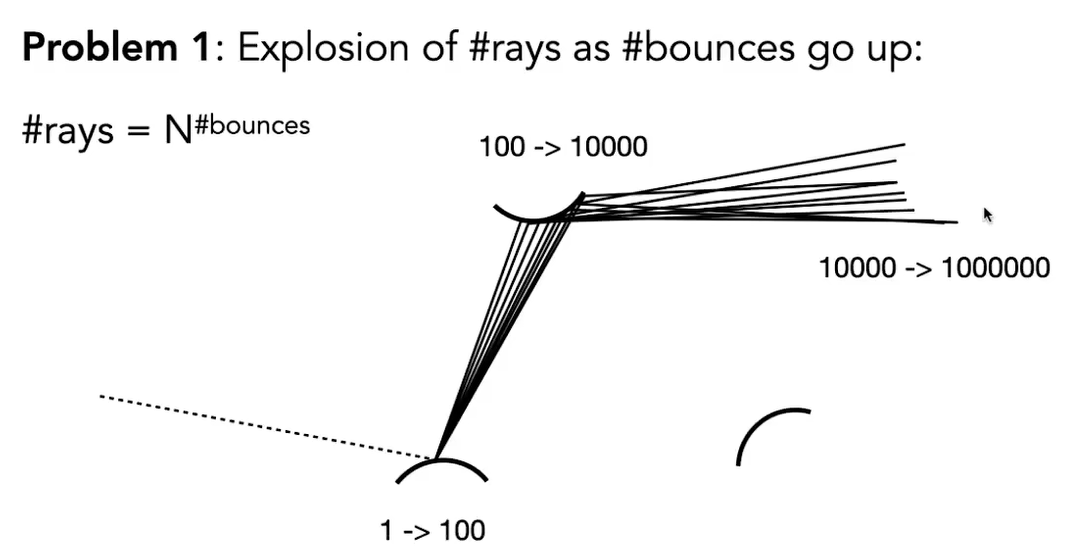
新的问题:
随着递归次数增加,光线数量爆炸
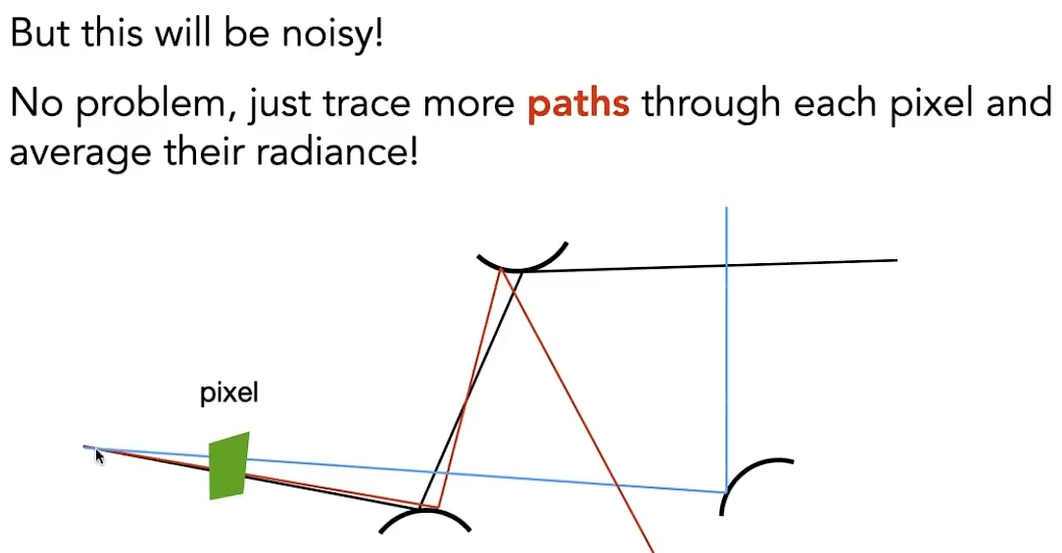
若只使用一根光线进行蒙特卡洛积分的采样,则光线数量不会爆炸
为了使结果有意义,使用更多的光线(路径)对同一个像素采样即可
新的算法依然是递归,且没有停止条件。若限制光线弹射次数,那么最终结果一定相比实际结果损失能量
使用“俄罗斯轮盘赌”方法,p 的概率返回值为 Lo/p ,1-p 的概率返回值为 0 ,如此一来结果的期望依然是 Lo ,即期望是实际结果
在上述算法中,蒙特卡洛积分在$2\pi$大小的立体角上随机采样,当光源小、少时效率低下,因此直接对光源采样
更改积分域
因此,对直接光照的计算只需要通过对光源采样,直接计算;而对间接光照,使用“俄罗斯轮盘赌”法,对$2\pi$立体角采样
在对光源采样时,需要从视点发出一根光线,检测和光源之间是否有阻挡
材质是物体与光线作用的方式,因此在物体表面,材质就是物体反射光的方式,就是 BRDF
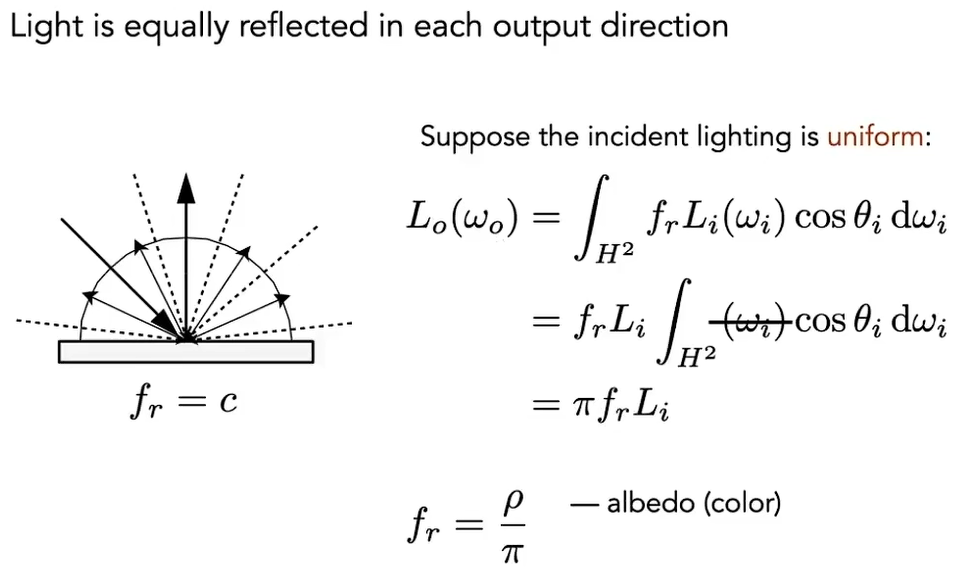
假设入射光在空间中均匀分布,出射光在半球面方向上($2\pi$立体角上)均匀分布,那么图中$f_r$,$L_i$是常数
若漫反射完全不损耗能量,那么$L_i=L_o$,得到$f_r=\frac{1}{\pi}$。若漫反射存在能量损耗,则$f_r=\frac{\rho}{\pi}$,其中$\rho$是反射率,可定义不同的颜色
入射角越大,反射的能量越多
菲涅尔项的准确计算和近似估计
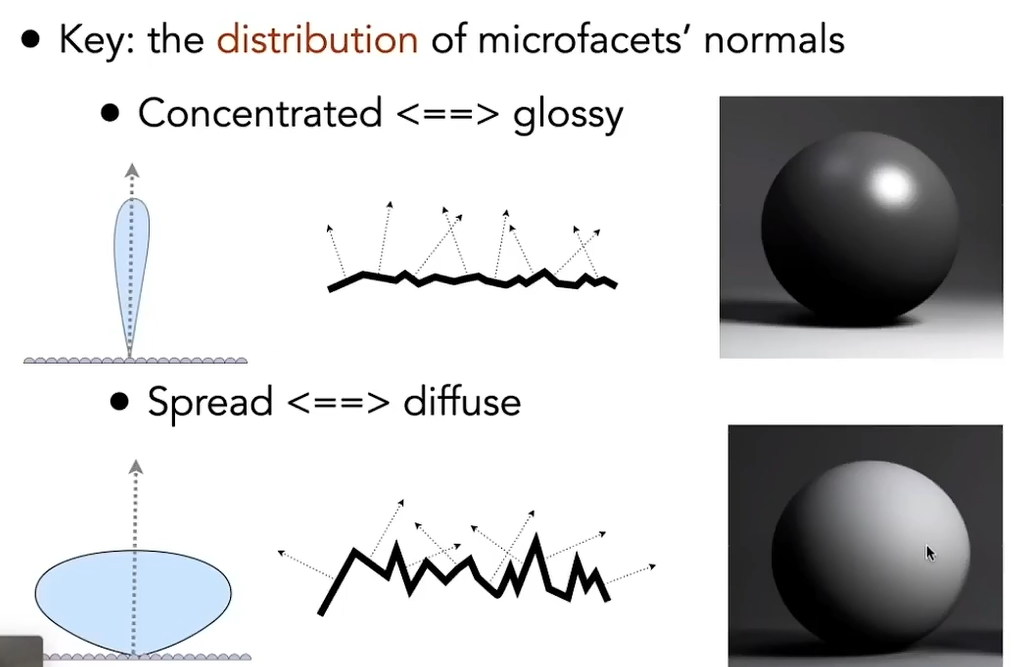
微表面模型(Microfacet Material) 远处观察到的是光滑物体表现出的不同的材质,近处观察到的不同的几何形状,材质的不同取决于物体微表面的几何形状
材质的粗糙程度取决于物体微表面的法线分布
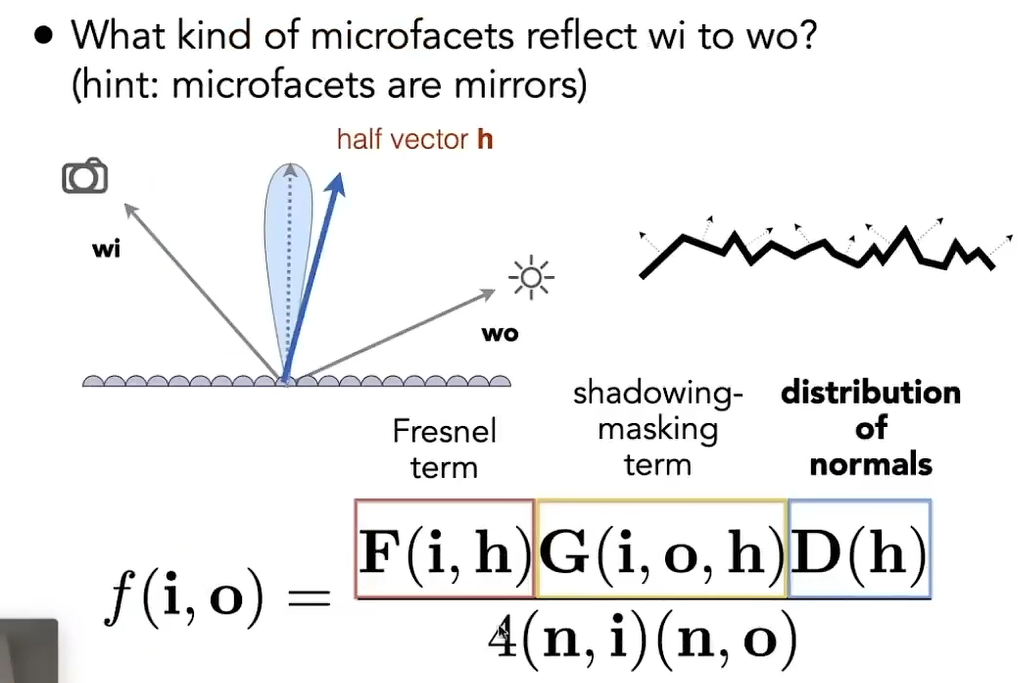
其中$D(h)$为微表面法线方向的分布函数,$h$为出射方向和入射方向的 half vector
在微表面模型中,只有法线方向和$h$相同的微表面才能将光线从入射方向反射到出射方向
其中$G(i,o,h)$为不同方向的微表面在反射时发生遮挡导致的损耗,在入射方向或出射方向几乎与法线方向垂直时,将产生较大遮挡损耗
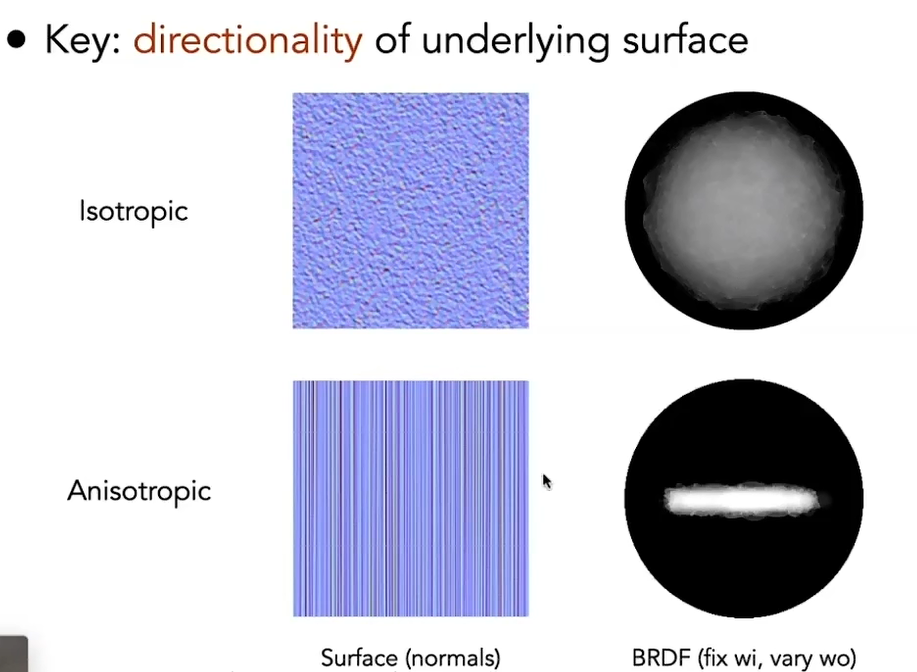
微表面模型可以用来描述各向异性材质
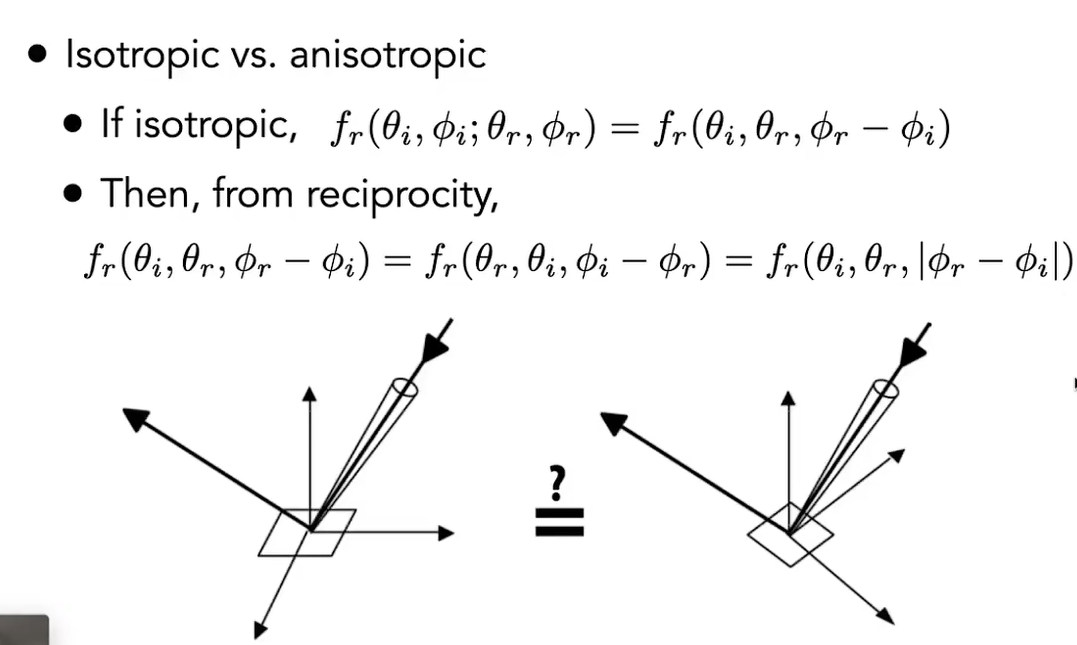
各向异性的 BRDF 与各向同性的 BRDF 的区别在于,各向同性的 BRDF 相当于是一个三元函数,且由光路可逆,具有良好的对称性
全光函数描述在空间中的任意一点,向任何一个方向看到的颜色(波长)信息,也即从任何方向接收到的颜色(波长)信息
光场可以用来描述物体在各个方向上被看到的信息
光场描述在任意位置上,向任意方向发出的光线的颜色(波长)信息
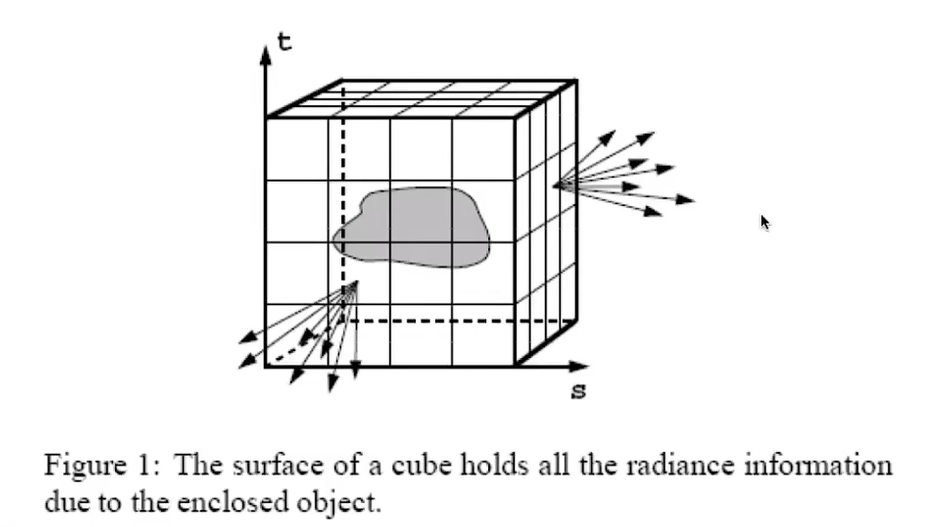
在物体的表面上取一包围盒,记录包围盒上任意一点向外发出的任意方向的光线的颜色(波长)信息,就是该物体的光场
光场通常是一个四维函数,描述方式有两种:
二维表面上的一点、球坐标方向
两个二维表面上的点形成光线方向