参见docs/图像处理大作业.pdf
首先确定圆的圆心,为测试图像的中心;然后确定圆的半径,为图像长、宽中的较小值。接下来根据圆的定义画圆:所有与圆心的距离等于半径的点构成一个圆。在这里,为了让画出的圆清晰可见,将所有与圆心距离在 0.98~1.02 倍半径之间的点全部标红,呈现在图像上。取出标红点的关键代码如下:
size_pic = size(hall_gray);
idx = zeros([size_pic, 2]);
for i = 1: 1: height
for j = 1: 1: width
idx(i, j, 1) = i;
idx(i, j, 2) = j;
end
end
circle_idx = ((idx(:, :, 1) - (height + 1) / 2) .^ 2 + (idx(:, :, 2) - (width + 1) / 2) .^ 2 <= (1.02 * radius) ^ 2 & ...
(idx(:, :, 1) - (height + 1) / 2) .^ 2 + (idx(:, :, 2) - (width + 1) / 2) .^ 2 >= (0.98 * radius) ^ 2);最后效果如下:
将测试图像分成 8*8 的区域,然后对每块区域根据国际象棋“黑白格”的规则染色。在黑色的地方,将原图对应区域置为0;白色的地方则保持不变。结果如下
本题代码位于src/hw1_3_2.m中。
图像的预处理是将每个像素灰度值减128,若要在变换域进行,可以利用DCT变换的线性性来操作。
首先对原图像作二维DCT变换,然后对相同大小的、所有元素均为128的矩阵作二维DCT变换。由于全128的矩阵DCT变换结果只有直流分量,即左上角元素,所以只需让原图的DCT变换结果的直流分量减去全128矩阵DCT变换结果的直流分量即可。具体代码如下:
[part_h, part_w] = size(hall_part);
DC_128 = dct2(zeros(part_h, part_w) + 128);
maphall_2 = dct2(hall_part);
maphall_2(1, 1) = maphall_2(1, 1) - DC_128(1, 1);这样操作后,与先预处理再DCT变换的结果相比,计算MSE,为 7.1000e-28,非常小,说明两种算法计算结果相同。
本题代码位于src/hw2_4_1.m中。
二维DCT变换,首先是找到DCT算子D。我直接根据指导书的公式(2.5),在matlab中实现算子D。关键代码如下:
function D_mat = DCT2_D(input_dim)
row = linspace(0, input_dim - 1, input_dim)';
col = linspace(1, input_dim * 2 - 1, input_dim);
cos_mat = cos(row * col * pi / (2 * input_dim));
cos_mat(1, :) = cos_mat(1, :) / sqrt(2);
D_mat = sqrt(2 / input_dim) * cos_mat;
end得到DCT算子D后,就可以根据输入图像的维度,计算二维DCT变换。假设灰度图像维度为 [height, width],则其二维DCT变换结果可以用以下代码来求得
[height, width] = size(input_mat);
dct_coef = DCT2_D(height) * double(input_mat) * DCT2_D(width)';我将我实现的DCT变换函数,与matlab提供的dct2进行比较,计算MSE,为9.9944e-26。MSE非常小,可以认为两种方法计算结果相同。
本题代码位于src/hw2_4_2.m中,计算DCT算子的函数封装在src/DCT2_D.m中,计算二维DCT变换的函数封装在src/DCT2.m中。
将原图按 8*8 分块后,对每块作二维DCT变换,再将DCT系数矩阵右侧四列、左侧四列系数矩阵分别置零,再作逆DCT变换看结果。
理论上分析,DCT系数矩阵左上角元素代表低频分量,右下方系数表示横竖两个方向中迅速变换的高频分量。由于常见的图片通常颜色、亮度都是缓慢变换的,因此DCT系数矩阵越往左上方取值越大,越向右下方取值越小。由于低频分量值大,对图像影响大,高频分量值小,对图像影响小,所以,理论分析DCT系数矩阵右侧四列元素置零对图像影响较小,左侧四列元素置零则会对图像有很大影响。实际结果也正是如此,结果如下:
本题代码位于src/hw2_4_3.m中。
若DCT系数矩阵C转置,考虑DCT变换的公式 $$ C=dct(P)=DPD^T\ P=idct(C)=D^TCD\ D^{-1}=D^T $$ 所以C转置后再逆变换,结果为 $$ D^TC^TD=(D^TCD)^T=P^T $$ 结果为原图的转置。
由于右上方的系数反映图像中横向变化的纹理强度,逆时针旋转90°后,原本右下方高频分量的元素来到了右上方。由于高频分量元素本身就较小,所以DCT系数矩阵逆时针旋转90°后再逆变换,得到的图像横向几乎不会变化,呈现很强的横向纹理。
若将DCT系数矩阵旋转180°,左上方低频分量将会和右下方高频分量换位,导致恢复的图像低频分量小,高频分量大,从而图像变化剧烈,呈现格子状的纹理。
实际运行时,结果与理论分析相近,如下
本题代码位于src/hw2_4_4.m中。
如果认为差分编码是一个系统,则这个系统方程为
$$
y(n)=x(n-1)-x(n)
$$
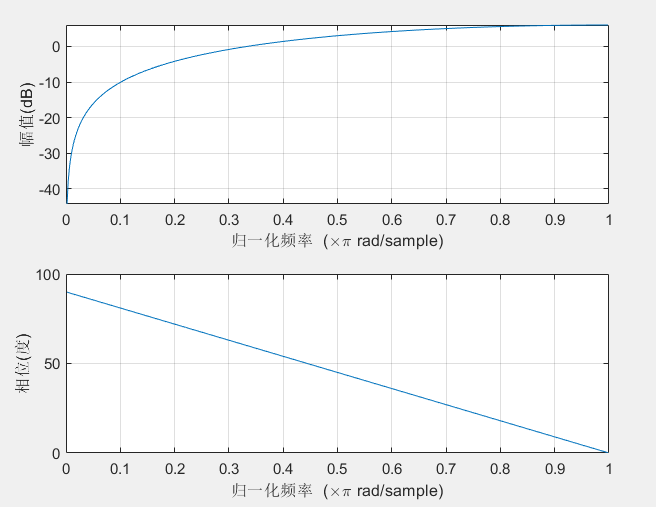
使用freqz函数查看该系统频率响应如下
由此可以看出,该系统可看作为高通滤波器。DC系数先进行差分编码再进行熵编码,说明DC系数含有较多的高频分量。
本题代码位于src/hw2_4_5.m中。
记DC预测误差为delta,Category为C,则它们之间的关系为
$$
C=ceil(log2(abs(delta)+1))
$$
由此可以推出,Category表示了DC预测误差的二进制表示位数。
由于本次作业中,只需对 8*8 的矩阵进行 Zig-Zag 扫描,因此可以直接将各索引手动编排好,然后直接用 matlab 的数组索引功能完成扫描。扫描代码如下
function output = zig_zag(input)
temp = reshape(input, [64, 1]);
output = (temp([
1, 9, 2, 3, 10, 17, 25, 18, ...
11, 4, 5, 12, 19, 26, 33, 41, ...
34, 27, 20, 13, 6, 7, 14, 21, ...
28, 35, 42, 49, 57, 50, 43, 36, ...
29, 22, 15, 8, 16, 23, 30, 37, ...
44, 51, 58, 59, 52, 45, 38, 31, ...
24, 32, 39, 46, 53, 60, 61, 54, ...
47, 40, 48, 55, 62, 63, 56, 64 ...
]));
end首先,我先将输入的 8*8 的矩阵变为 64*1 的大小。然后,我根据 Zig-Zag 的规则,事先将理论的 Zig-Zag 扫描结果的各位置索引记好。最后,即可直接通过数组索引的方式完成扫描。
为了验证我这一算法是正确的,我设计了如下测试样例进行检验
test_input = [
[1, 2, 6, 7, 15, 16, 28, 29]; ...
[3, 5, 8, 14, 17, 27, 30, 43]; ...
[4, 9, 13, 18, 26, 31, 42, 44]; ...
[10, 12, 19, 25, 32, 41, 45, 54]; ...
[11, 20, 24, 33, 40, 46, 53, 55]; ...
[21, 23, 34, 39, 47, 52, 56, 61]; ...
[22, 35, 38, 48, 51, 57, 60, 62]; ...
[36, 37, 49, 50, 58, 59, 63, 64] ...
];这一矩阵经过 Zig-Zag 扫描后,理论上应该输出 1~64 的序列,使用我设计的算法扫描得到结果正是如此,说明算法实现无误。
本题代码位于src/hw2_4_7.m中。
首先是预处理,灰度图各像素减去128;然后是将图像每个 8*8 的块进行DCT变换并点除量化矩阵;最后是将结果依次排列。
前两步的代码如下
hall_pre = double(hall_gray) - 128;
hall_quan = blockproc(hall_pre, [8, 8], @(mat)(zig_zag(round(dct2(mat.data) ./ QTAB))));重新排列时,我按照从左至右、从上至下的方式来遍历,代码如下
[height, width] = size(hall_quan);
res = zeros([64, height * width / 64]);
for i = 0: 1: height / 64 - 1
for j = 1: 1: width
res(:, i * width + j) = hall_quan(i * 64 + 1: (i + 1) * 64, j);
end
end本题代码位于src/hw2_4_8.m中。
关键点在于计算DC系数的码流和AC系数的码流。
首先是DC系数码流。DC系数就是第8问中量化矩阵的第一行,码流的计算需要先通过差分编码再进行熵编码。
熵编码时,可以利用DC预测误差与Category的关系:Category表示了DC预测误差的二进制表示位数,并利用给好的Huffman编码表DCTAB进行编码。对于每个预测误差,首先根据其Category确定对应的Huffman编码,然后将其幅度用二进制表示,接在其Huffman编码后。若幅度为0,无需编码幅度,Huffman编码已经包含了该信息。对于负数,幅度采用1补码,此时最高位为0。这样的方式表示每个预测误差,可以准确无误并容易解码。代码如下,其中quan_mat为量化矩阵:
dc_cof = quan_mat(1, :)';
dc_diff = [dc_cof(1); dc_cof(1: end - 1) - dc_cof(2: end)];
dc_category = min(ceil(log2(abs(dc_diff) + 1)), 11);
dc_code = [];
for i = 1: 1: length(dc_diff)
cat_temp = DCTAB(dc_category(i) + 1, 2: DCTAB(dc_category(i) + 1, 1) + 1)';
if dc_diff(i) ~= 0
mag_temp = dec2bin(abs(dc_diff(i)))' - '0';
if dc_diff(i) < 0
mag_temp = ~mag_temp;
end
else
mag_temp = [];
end
dc_code = [dc_code; cat_temp; mag_temp];
endAC系数编码与DC系数稍有不同。AC系数是量化矩阵第2行及之后的元素,需要根据每一个非零系数值及其行程进行编码。AC系数中可能有较多的0,因此利用行程编码能较好地提高压缩率。我们通过提供的ACTAB,以非零数值与行程为索引,找到对应的Huffman编码,然后再在其后接上非零数值的二进制表示(负数为1补码),从而完成对AC系数的编码。
这其中用到两个符号:
- ZRL:[1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1],表示连续 16 个 0
- EOB:[1, 0, 1, 0],表示每个块中编码完最后一个非零系数
我采用这样的方式进行编码:对每个块(也就是 63*1 的列),遍历时实时记录经过的零个数,当到第一个非零数值时,对记录的零个数求除 16 的商与余数,商为需要加上的 ZRL 的个数,余数为用于提供Huffman编码的索引,即行程。若一直到每个块最后,都没找到非零数值,则码流中添加 EOB 。
求解AC码流的代码如下
ac_cof = quan_mat(2: end, :);
ac_size = min(ceil(log2(abs(ac_cof) + 1)), 10);
ZRL = [1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1]';
EOB = [1, 0, 1, 0]';
[ac_h, ac_w] = size(ac_size);
ac_code = [];
for i = 1: 1: ac_w
run = 0;
for j = 1: 1: ac_h
if ac_size(j, i) == 0
run = run + 1;
else
run_epoch = floor(run / 16);
run_mod = mod(run, 16);
run = 0;
while run_epoch > 0
ac_code = [ac_code; ZRL];
run_epoch = run_epoch - 1;
end
size_temp = ACTAB(run_mod * 10 + ac_size(j, i), 4: ACTAB(run_mod * 10 + ac_size(j, i), 3) + 3)';
amp_temp = dec2bin(abs(ac_cof(j, i)))' - '0';
if ac_cof(j, i) < 0
amp_temp = ~amp_temp;
end
ac_code = [ac_code; size_temp; amp_temp];
end
end
ac_code = [ac_code; EOB];
end 至此,就完成了DC码流与AC码流的计算。
本题代码位于src/hw2_4_9.m中,编码函数封装在函数文件src/Compress.m中。
计算时需统一单位,我这里用 bit 计算。原图 1 像素为 0~255,用 8bits 储存,因此压缩比计算公式为
compress_rate = img_height * img_width * 8 / (length(dc_code) + length(ac_code));计算结果为:6.4247
本题代码位于src/hw2_4_10.m中。
解码需分别对DC码流与AC码流解码。
由于Huffman编码为前缀编码,任何码字都不是其他码字的前缀,因此解码起来比较简单。对于一段码字,只要在Huffman编码表中匹配上了,那由于前缀码的特性,这段码字就是一段Huffman码。
因此,对DC码流进行解码时,逐段码流和Huffman编码表DCTAB进行比对,一旦比对上了,就反推这段码流对应的Category,然后接下来的长为Category的码流,代表的就是幅度。如果首位是1,则是正幅度;首位是0,则是负幅度;Category若为0,则幅度就为0。对整个DC码流进行如上遍历操作,很容易就将DC码流解码完成。解码完成后,得到的是差分编码后的结果,然后还要将差分编码再解码,得到原始的DC系数。代码如下
dc_diff = zeros([img_height * img_width / 64, 1]);
last_idx = 1;
cnt = 1;
i = 1;
while i <= length(dc_code)
for j = 1: 1: size(DCTAB, 1)
if isequal(dc_code(last_idx: i)', DCTAB(j, 2: DCTAB(j, 1) + 1))
if j - 1 ~= 0
mag_temp = dc_code(i + 1: i + j - 1)';
if mag_temp(1) == 1
dc_diff(cnt) = bin2dec(char(mag_temp + '0'));
else
dc_diff(cnt) = -bin2dec(char(~mag_temp + '0'));
end
end
last_idx = i + j;
i = i + j;
cnt = cnt + 1;
break;
end
end
i = i + 1;
end
dc_cof = zeros(size(dc_diff));
dc_cof(1) = dc_diff(1);
for i = 2: 1: size(dc_cof, 1)
dc_cof(i) = dc_cof(i - 1) - dc_diff(i);
endAC码流解码过程类似,不过得注意两个特殊符号:ZRL 和 EOB。AC码流解码过程中,不仅要在Huffman编码表中去比对,也要与 ZRL 和 EOB 去比对,其余步骤和DC码流解码思路一样。代码如下
ac_cof = zeros([63, img_height * img_width / 64]);
i = 1;
last_idx = 1;
row_cnt = 1;
col_cnt = 1;
while i <= length(ac_code)
if isequal(ac_code(last_idx: i), EOB)
col_cnt = col_cnt + 1;
row_cnt = 1;
last_idx = i + 1;
i = last_idx;
elseif isequal(ac_code(last_idx: i), ZRL)
row_cnt = row_cnt + 16;
last_idx = i + 1;
i = last_idx;
else
for j = 1: 1: size(ACTAB, 1)
if isequal(ac_code(last_idx: i)', ACTAB(j, 4: ACTAB(j, 3) + 3))
row_cnt = row_cnt + ACTAB(j, 1);
amp_temp = ac_code(i + 1: i + ACTAB(j, 2))';
if amp_temp(1) == 1
ac_cof(row_cnt, col_cnt) = bin2dec(char(amp_temp + '0'));
else
ac_cof(row_cnt, col_cnt) = -bin2dec(char(~amp_temp + '0'));
end
row_cnt = row_cnt + 1;
last_idx = i + ACTAB(j, 2) + 1;
i = last_idx;
break;
end
end
end
i = i + 1;
end得到解码后DC码流和AC码流后,两者合并得到量化矩阵,再经过第8问的逆过程与逆DCT变换,即可解码出原图。代码如下
whole_cof = [dc_cof'; ac_cof];
hall_quan = zeros([img_height * 8, img_width / 8]);
for i = 0: 1: img_height / 8 - 1
hall_quan(i * 64 + 1: (i + 1) * 64, :) = whole_cof(:, i * img_width / 8 + 1: (i + 1) * img_width / 8);
end
img = uint8(blockproc(hall_quan, [64, 1], @(mat)(idct2(inv_zig_zag(mat.data) .* QTAB))) + 128);接下来是评价编解码效果。
客观方法计算PSNR,PSNR计算公式为 $$ PSNR=10lg(\frac{255^2}{MSE}) $$ 实际计算结果为:31.1874,是一个比较高的结果,因此说明图像失真较小。
主观上,原图与编解码后的图片如下
二者差别不大,只在一些细微处有少许差别,说明压缩后图像失真较小。
本题代码位于src/hw2_4_11.m中,解码代码封装在函数文件src/Decompress.m中。
要让量化步长减半,只需让提供的QTAB除以2即可。
量化步长减半后,PSNR从31.1874变为34.2067,图像失真程度减少;但压缩比从6.4247降低到4.4097,压缩程度减少。这说明,要保持高的压缩比,就要牺牲图像的还原度。
本题代码位于src/hw2_4_12.m中。
对雪花图像编解码,原图与解码图像如下
压缩比为 3.645,PSNR 为 22.9244。
可以看到,PSNR不算大,压缩比也较小。原因是,雪花图像并不美丽,像是随机生成的噪音,高频分量大,导致量化后 Category 可能偏大,导致 Huffman 编码较长,压缩比较小。同时由于高频分量经过量化后,失真较大,因此 PSNR 较小。
本题代码位于src/hw2_4_13.m中。
空域信息隐藏,是将信息表示成二进制码流,再二进制码流的每位信息替换图像中各像素亮度分量的最低位。这一操作使用 matlab 提供的 bitset函数即可实现。代码如下
rand_info = logical(randi([0, 1], height, width));
hall_hide = bitset(hall_gray, 1, rand_info);经过编解码后,要再提取出隐藏的信息时,使用 matlab 提供的bitand方法,即可实现信息提取。
[dc_code, ac_code, img_height, img_width] = Compress(hall_hide, DCTAB, ACTAB, QTAB);
hall_decompress = Decompress(dc_code, ac_code, img_height, img_width, DCTAB, ACTAB, QTAB);
decode_info = bitand(hall_decompress, uint8(ones([height, width])));经过提取后,与原本隐藏的信息进行对比,准确率大约在 50% 左右,和随机蒙的差不多,说明其抗 JPEG 编码能力极差。
本题代码位于src/hw3_4_1.m中
方法一:信息位替换量化后DCT系数的最低位。关键代码如下
hall_pre = double(img) - 128;
hall_quan = blockproc(hall_pre, [8, 8], @(mat)(zig_zag(round(dct2(mat.data) ./ QTAB))));
[height, width] = size(hall_quan);
quan_mat = zeros([64, height * width / 64]);
for i = 0: 1: height / 64 - 1
for j = 1: 1: width
quan_mat(:, i * width + j) = hall_quan(i * 64 + 1: (i + 1) * 64, j);
end
end
quan_mat = double(bitset(int32(quan_mat), 1, info));方法二:信息位替换若干量化后DCT系数。我这里选用量化系数中,较小值的位置去替换量化后DCT系数,这样对原图的影响较小。
确定替换位置的方法如下
threshold = 12;
less_thre = QTAB <= threshold;
less_thre_idx = find(less_thre);然后根据选取的位置,用信息位去替换
hall_pre = double(img) - 128;
hall_quan = blockproc(hall_pre, [8, 8], @(mat)(zig_zag(round(dct2(mat.data) ./ QTAB))));
[height, width] = size(hall_quan);
quan_mat = zeros([64, height * width / 64]);
for i = 0: 1: height / 64 - 1
for j = 1: 1: width
quan_mat(:, i * width + j) = hall_quan(i * 64 + 1: (i + 1) * 64, j);
end
end
last_bit = bitand(int32(quan_mat), int32(ones(size(quan_mat))));
for i = 1: 1: size(last_bit, 2)
last_bit(hide_idx, i) = info(:, i);
end
quan_mat = double(bitset(int32(quan_mat), 1, last_bit));方法三:隐藏信息用1,-1序列表示,再逐一将信息位追加在每个块 Zig-Zag 顺序的最后一个非零系数后;若原本该最后一个系数不为0,那就用信息位替换该系数。关键代码如下
hall_pre = double(img) - 128;
hall_quan = blockproc(hall_pre, [8, 8], @(mat)(zig_zag(round(dct2(mat.data) ./ QTAB))));
[height, width] = size(hall_quan);
quan_mat = zeros([64, height * width / 64]);
for i = 0: 1: height / 64 - 1
for j = 1: 1: width
col_temp = i * width + j;
quan_mat(:, col_temp) = hall_quan(i * 64 + 1: (i + 1) * 64, j);
for k = 64: -1 : 1
if quan_mat(k, col_temp) ~= 0
if k == 64
quan_mat(64, col_temp) = info(col_temp);
else
quan_mat(k + 1, col_temp) = info(col_temp);
end
break;
end
end
end
end三种方法实现起来都比较简单,其信息隐藏部分分别封装在函数文件dct_conceal_1.m、dct_conceal_2.m、dct_conceal_3.m中,将信息隐藏后的系数逆变换为图片的代码,分别封装在函数文件dct_reveal_1.m、dct_reveal_2.m、dct_reveal_3.m中。
三种方法隐藏随机信息后,客观上的对比如下
可以看到,ACC都是1,压缩率第一种方法最小。总体来看,第二种和第三种方法效果差不多。
三种方法隐藏随机信息后,呈现的图片结果如下
主观上从图片上看,用第一种方法隐藏信息的结果较差,第二、第三种方法效果差不多。理论上分析,由于直接在量化后的矩阵加信息位,如果量化系数较大,则最后一位改为信息位后,对原图的影响较大。而第二种方法则是考虑了这一影响,选择了QTAB中元素较小的位置进行信息隐藏,这样就对原图的影响较小。第三种方法也是类似的思路,由于1与-1的变化对整个系数矩阵影响较小,所以信息隐藏后对原图也不会有太大影响。
本题代码位于src/hw3_4_2.m中。
如果样本人脸大小不一,图像不需要首先调整为相同大小,只需对每个像素的颜色遍历即可。
训练人脸标准时,需要将RGB颜色对应到颜色数n,代码为
r = floor(face_temp(j, k, 1) * 2^(L - 8));
g = floor(face_temp(j, k, 2) * 2^(L - 8));
b = floor(face_temp(j, k, 3) * 2^(L - 8));
n = r * 2^(2 * L) + g * 2^L + b;然后根据颜色索引 n,统计各个颜色出现的频率,然后再对该频率向量归一化,得到一张图片的人脸标准。
对每张训练集图片都计算相应的人脸标准向量,然后取平均,得到训练好的人脸标准向量。
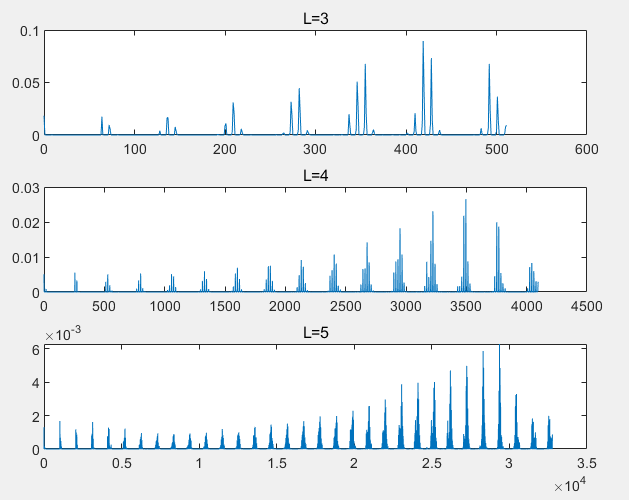
对于 L 为 3,4,5 的情况,将对应的人脸标准绘成图,如下
可以看到,不同的 L 值,人脸特征的趋势是一致的。L 值越大,颜色区分能力越强,分辨率越高。对于较小的 L 值,会使大范围内相近的颜色不能被区分开。同时,对于较高的 L 值,相近的颜色范围内求和就会得到较低的 L 值的图像。
本题代码位于src/hw4_3_1.m中。
首先,我们使用人脸图像训练集训练人脸特征向量,然后使用该特征向量进行进一步人脸检测。
我设计的人脸检测算法,先用小矩形在图像上移动,逐个计算小矩形内的颜色特征向量,然后与训练的人脸特征向量计算距离,距离公式为 $$ d(u,v)=1-\Sigma_n\sqrt{(u_n,v_n)} $$ 将所有与人脸特征向量距离小于阈值的小矩形,全部存储下来。由于小矩形移动时,会有一定的重叠。下一步就是将所有重叠的矩形,整合成一个大矩形。这里使用的是暴力遍历,对每个储存下来的小矩形,与其他所有矩形进行比较,将所有可以合成的小矩形一并合成,计算复杂度为 O(n^2) 。代码如下
for i = 1: 1: length(x_less)
if x_less(i) ~= -1
for j = i + 1: 1: length(x_less)
if j ~= i && x_less(j) ~= -1
if x_less(i) == x_less(j)
if y_less(j) <= y_large(i) + col_width && y_less(j) >= y_less(i)
y_large(i) = y_large(j);
x_large(i) = max(x_large(i), x_large(j));
x_less(j) = -1;
end
end
if y_less(i) == y_less(j)
if x_less(j) <= x_large(i) + row_width && x_less(j) >= x_less(i)
x_large(i) = x_large(j);
y_large(i) = max(y_large(i), y_large(j));
x_less(j) = -1;
end
end
end
end
end
end使用这种二维遍历合并小矩形后,部分区域会产生重叠的大矩形。接下来,为了呈现良好的人脸检测效果,需要将重叠的大矩形去重。重叠的情况我分为以下几种:
情况一:角重叠
情况二:中心重叠
情况三:一边重叠
我根据重叠的面积占大矩形面积的比例,来判断两个矩形的重叠程度。如果重叠程度过大,则舍弃其中一个矩形,因为它们很可能是识别出的同一个人脸。至此,可以认为剩余的矩形都不再重叠。
然后,我移除那些面积较小的矩形,因为面积过于小的矩形一般来说识别的并不是人脸。
最后,我对所有检测矩形进行优化。我将窄而长的矩形稍微压缩一下,尽可能压成正方形。同时,矩形的中心要稍稍上移。这是因为,检测算法是根据肤色来确定的,而脖子部分和人脸的颜色接近,人脸检测时,容易将脖子也一并识别,所以矩形可能会呈现窄而宽,且中心偏下。如下图所示
当然,如果一个矩形宽而矮,我也会进行一定的压缩一下,让它更接近正方形。
至此,就完成了人脸检测的工作。
对于 L=3,4,5 ,人脸检测的效果如下
可以看到,对于大部分人脸识别效果都是不错的。少部分人脸由于靠的太近或衣服颜色问题,部分人脸被识别在了一起,但总体效果还是可以的。
在人脸检测过程中,我将小矩形的长宽都定为20,移动步长为5,面积重叠比例大于0.01则认为识别了同一张人脸。L=3,4,5 时,距离相近的阈值分别为 0.053,0.603,0.750,逐步上升。
本题代码位于src/hw4_3_2.m中,人脸检测算法封装在函数文件src/DetectFace.m中,测试图像为图像处理所需资源/test1.png。
使用imrotate方法将图片旋转,使用imresize方法将图片拉长,使用imadjust方法将图片变色,再进行人脸检测。参数采用 L=3 。结果如下
旋转90°:
拉长一倍:
变色:
从识别结果看,旋转90°的识别结果和原本的识别结果较不一样。拉长一倍和变色后,识别结果都和原本的识别结果相近,且拉长一倍后检测效果有所改善。
理论上分析,旋转90°后,由于图像色彩没有变化,所以人脸检测中储存的小矩形应当是和原本图像的结果是一样的。但是由于图像旋转了90°,导致合并小矩形以及之后的去重大矩形的过程中,和原图的结果不一致,导致最后的检测结果和原图不一致。
图像拉长一倍后,原本图像相近的色彩,在图像被拉长后,也显得容易区分了。所以在原本 L=3 的情况下区分不开的人脸,在图像被拉长后也能区分出来了。
在图像稍微变色后,识别结果和原图区别不大。这是因为图像整体颜色的改变,相当于人脸颜色整体改变,在多维空间中的人脸向量与未改变颜色前的向量,应当是平行关系。而检测距离是与检测的人脸向量和训练的标准向量的夹角有关的。整体改变颜色,不改变这个夹角,所以距离是基本不会变的。因此,图像稍微变色,对识别结果不会有太大的影响。
本题代码位于src/hw4_3_3.m中
在进行人脸检测的实验时,由于仅仅是根据肤色去判断,因此人的手、脖子等与脸颜色接近的部分,也会被识别为人脸。而且如果有些人戴了眼镜,由于训练样本戴眼镜的较少,所以眼镜对识别结果也会有一些影响。因此,如果重新选择人脸样本训练标准的话,除了肤色,可能还得考虑人脸的进阶特征。具体方法是,首先通过肤色初筛人脸区域,然后进一步考虑识别的人脸区域有没有五官特征。五官特征可以由训练图像的梯度进行判断。