This is an open source initiative to make available the tools required for building your own optimal Markowitz portfolios and finding the best rebalancing strategy factoring in your transaction costs. The financial world is moving towards zero cost ETFs, which make even the lowest-cost robo-advisors in the industry seem expensive.
The mission of this project is to put industry leading portfolio management tools into the hands of individuals for zero cost.
In this example we build a portfolio with no asset size constraints. Meaning, a single ETF or stock from our list can be 100% of the portfolio.
from roboadvisor.optimizer import PortfolioOptimizer
assets=['TLT','SPY','GDX','AAPL','FXI','GLD','VDE','UUP','VT']
optimal_portfolio=PortfolioOptimizer(assets, portfolio_size=5,max_pos=1.0, min_pos=0.0)...Maximum position size: 100%
...Minimum position size: 0%
...Number of unique asset combinations: 126
...Analyzing 126 of 126 asset combinations...
...Omitted assets: []
-----------------------------------------------
----- Portfolio Optimized for Sharpe Ratio ----
-----------------------------------------------
('TLT', 0.3207)
('SPY', 0.1373)
('AAPL', 0.1723)
('GLD', 0.0711)
('UUP', 0.2987)
Optimal Portfolio Return: 7.4065
Optimal Portfolio Volatility: 7.1075
Optimal Portfolio Sharpe Ratio: 1.0421
-----------------------------------------------
----- Portfolio Optimized for Pure Return -----
-----------------------------------------------
('AAPL', 1.0)
('GLD', 0.0)
('VDE', 0.0)
('UUP', 0.0)
('VT', 0.0)
Optimal Portfolio Return: 22.6168
Optimal Portfolio Volatility: 29.8647
Optimal Portfolio Sharpe Ratio: 0.7573
-----------------------------------------------------
----- Portfolio Optimized for Minimal Volatility ----
-----------------------------------------------------
('TLT', 0.1644)
('SPY', 0.0)
('GLD', 0.1268)
('UUP', 0.5449)
('VT', 0.1638)
Optimal Portfolio Return: 2.755
Optimal Portfolio Volatility: 4.651
Optimal Portfolio Sharpe Ratio: 0.5924
In this example we're going to constrain the maximum position size of a single asset to be 30%, and the minumum size to be 5%.
assets = ['TLT','SPY','GDX','AAPL','FXI','GLD','VDE','UUP','VT','IYF','EWI','TIP']
optimal_portfolio = PortfolioOptimizer(assets, portfolio_size = 5, max_pos = 0.30, min_pos = 0.05)...Maximum position size: 30%
...Minimum position size: 5%
...Number of unique asset combinations: 792
...Analyzing 792 of 792 asset combinations...
...Omitted assets: []
-----------------------------------------------
----- Portfolio Optimized for Sharpe Ratio ----
-----------------------------------------------
('TLT', 0.1981)
('SPY', 0.1089)
('AAPL', 0.1495)
('UUP', 0.2435)
('TIP', 0.3)
Optimal Portfolio Return: 6.5281
Optimal Portfolio Volatility: 6.1652
Optimal Portfolio Sharpe Ratio: 1.0589
-----------------------------------------------
----- Portfolio Optimized for Pure Return -----
-----------------------------------------------
('TLT', 0.05)
('SPY', 0.3)
('AAPL', 0.3)
('VT', 0.05)
('IYF', 0.3)
Optimal Portfolio Return: 12.1792
Optimal Portfolio Volatility: 21.8554
Optimal Portfolio Sharpe Ratio: 0.5573
-----------------------------------------------------
----- Portfolio Optimized for Minimal Volatility ----
-----------------------------------------------------
('TLT', 0.1276)
('SPY', 0.1693)
('GLD', 0.1031)
('UUP', 0.3)
('TIP', 0.3)
Optimal Portfolio Return: 3.6682
Optimal Portfolio Volatility: 4.3676
Optimal Portfolio Sharpe Ratio: 0.8399
The intention of the rebalancer class is to understand, probabilistically, how the portfolio should be maintained going forward. It also reveals how much value might be added for the client depending on the advisory model and management principles.
The class can account for the following parameters:
- High Threshold: The upper deviation, as a percentage, that a single issue can drift before rebalancing is triggered.
- Low Threshold: The lower deviation, as a percentage, that a single issue can drift before rebalancing is triggered.
- Trade cost: Cost to execute a single trade, including commissions.
- Fractional Units: Whether or not you are permitted to buy fractional units.
- Starting cash balance: The cash balance to begin the portfolio simulation with.
- Slippage (optional): A custom function can be presented to represent deviations from bid/ask.
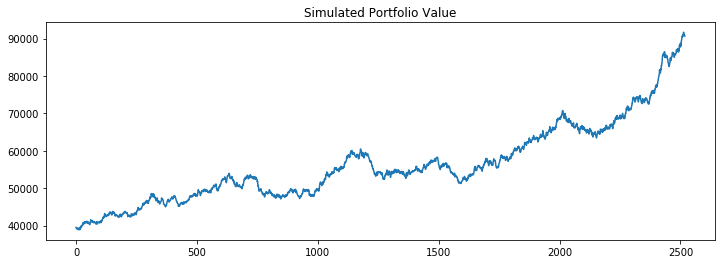
The rebalancer class takes a portfolio object as an argument as well. The simulation in this example runs over 10 years (2520 trading days).
from roboadvisor.rebalancer import RebalancingSimulator
from roboadvisor.optimizer import PortfolioOptimizer
assets = ['GLD', 'SPY', 'TLT', 'QQQ', 'XLI']
portfolio = PortfolioOptimizer(assets , portfolio_size = 5, max_pos = 0.3, min_pos = 0.05)
rebalancer = RebalancingSimulator(portfolio, frac_units=False, trade_cost=5.99, starting_cash=20000, max_thresh=1.1, min_thresh=0.9)
rebalancer.run_simulation()SIMULATION PARAMETERS:
...fractional share purchases permitted? False
...portfolio size: 5 assets
...trade cost: $5.99
...max position size: 30%
...min position size: 5%
...beginning cash value: $20,000
...upper rebalance trigger: 10% above allocation
...lower rebalance trigger: 10% below allocation
...Cash balance after portfolio initialization: $388.99
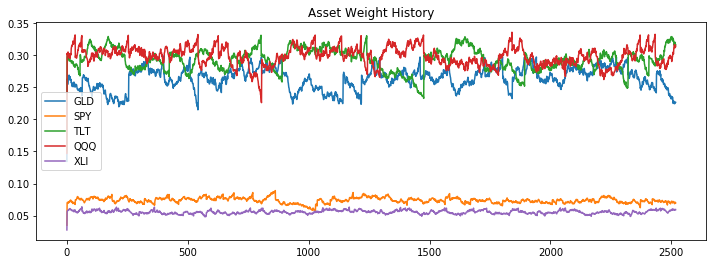
Target weights: [('GLD', 26.93%), ('SPY', 7.51%), ('TLT', 30%), ('QQQ', 30%), ('XLI', 5.57%)]
SIMULATION REPORT
-----------------
Rebalancing simulation finished in: 0.73 seconds
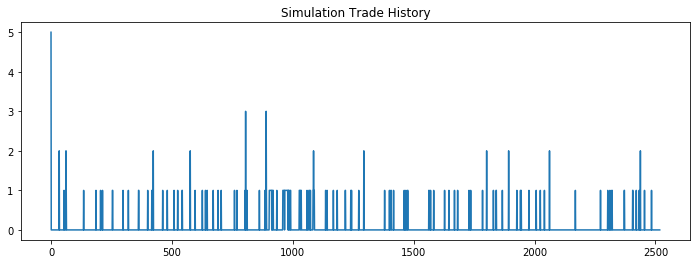
Total number of trades executed: 178
Cost per trade: 5
Total trading costs: 890
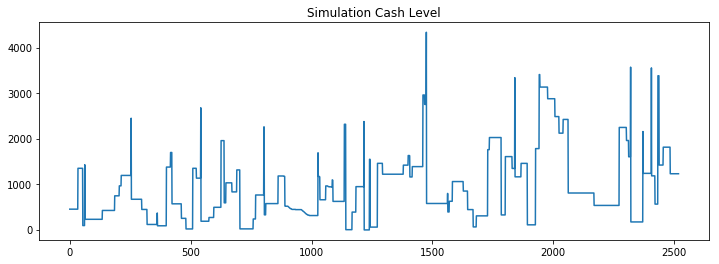
Maximum cash balance: 4337.12
Minimum cash balance: -5.96
Average cash balance: 881.49
Fractional units allowed? False
Weight metrics for: GLD
-------------------------
Target portfolio weight: 0.2693
Standard deviation of GLD portfolio weight: 0.0168
Maximum weight reached for GLD: 0.2989
Minimum weight reached for GLD: 0.1347
Average of GLD portfolio weight: 0.2637
Weight metrics for: SPY
-------------------------
Target portfolio weight: 0.0751
Standard deviation of SPY portfolio weight: 0.0043
Maximum weight reached for SPY: 0.089
Minimum weight reached for SPY: 0.035
Average of SPY portfolio weight: 0.0738
Weight metrics for: TLT
-------------------------
Target portfolio weight: 0.3
Standard deviation of TLT portfolio weight: 0.0173
Maximum weight reached for TLT: 0.3314
Minimum weight reached for TLT: 0.1489
Average of TLT portfolio weight: 0.2929
Weight metrics for: QQQ
-------------------------
Target portfolio weight: 0.3
Standard deviation of QQQ portfolio weight: 0.0147
Maximum weight reached for QQQ: 0.3361
Minimum weight reached for QQQ: 0.1471
Average of QQQ portfolio weight: 0.2985
Weight metrics for: XLI
-------------------------
Target portfolio weight: 0.0557
Standard deviation of XLI portfolio weight: 0.0027
Maximum weight reached for XLI: 0.0637
Minimum weight reached for XLI: 0.0276
Average of XLI portfolio weight: 0.0556