1. Dijkstra最短路径算法

Dijkstra最短路径算法可以用于在图中查找从某一点出发，到另外一个点距离最短的路径。

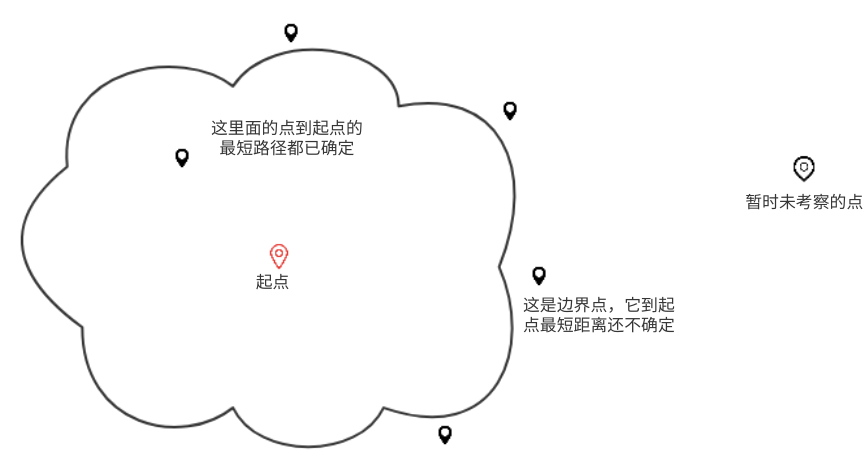
它的核心思想是，以起始点为中心，逐步确定外围的点到它的最短路径，向外层层推进直到覆盖到目标点，或者全图搜索完毕仍未找到终点（此时每个点到起点的最短路径均被计算出来）

算法思路：

• 为了方便，将图中n个点分别记为1,2,3,...,n。
• 为了描述方便，将一个点到起点的最短距离简单称为该点的最短距离。
• 数组Dis保存每个点的最短距离。
• 数组Bound保存当前正在考察的边界点。边界以内的所有点都已经确定了最短距离。

1. 先将数组Dis的所有元素初始化为INF（无穷大）。将每个点标记为未确认状态。
2. Dis(s)设值为0，将s添加到Bound数组待考察。
3. 从Bound数组取出目前距起点最近的点m，将该点标记为已确认状态。
4. 检查m是否为终点。如果是则退出当前算法，输出最短路径；否则进入下一步。
5. 将m点相邻的所有未确认的点放入Bound数组，并更新这些点的最短距离（即是否经过m到这些点最短距离更小）。
6. 如果Bound数组为空，则退出该算法，终点不在图内；否则，回到步骤3.