A collection of pure Java programs implementing sequences from The On-Line Encyclopedia of Integer Sequences (OEIS).
This is likely the largest coherent collection of programs for OEIS sequences beyond the Maple, Mathematica, and Pari programs directly associated with many entries. Currently over 150,000 sequences are implemented.
If you plan to simply run some existing sequences, then the best option is to download the latest release.
Instructions for installation: INSTALLATION
Notes on development: DEVELOPMENT
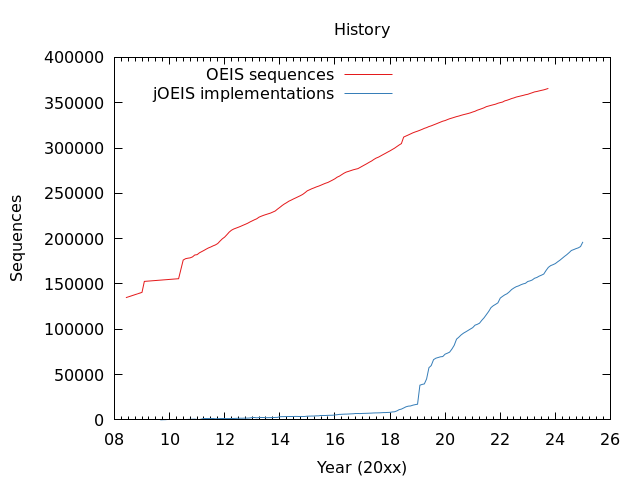
The following plot shows how the number of implemented sequences has changed over the years.
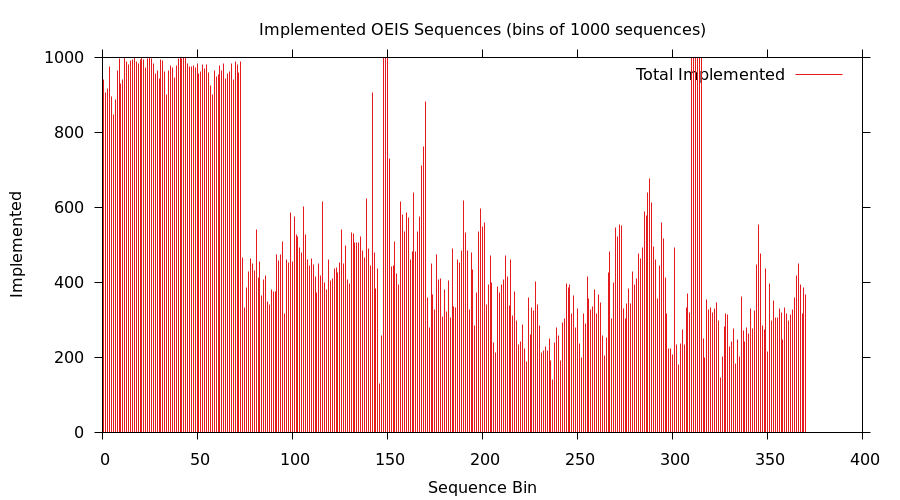
The following plot shows the number of sequences implemented (in bins of 1000):
A similar plot with one pixel for each sequence. Green indicates an implemented sequence. Black indicates to be done, feel free to help.
Implementations are not necessarily the best known algorithm for
particular sequences. For many important sequences you are not going
to be able to compute new terms using the implementations provided.
However, included here are implementations that have been used to
compute new previously unknown terms, including some for sequences
considered hard.
Because Java does not come with libraries supporting all the things we need to do to construct integer sequences, a lot of functionality has been built from the ground up. While a lot of this is implemented specifically for this project, there are important pieces of code which have been re-implemented or ported from other projects.
Although Java has its own BigInteger class for large integers, this
project uses a big integer type, Z.java based originally on
Lenstra's lip C package.
Most sequences requiring real number arithmetic are handled using classes based on Hans-J. Boehm's constructible real arithmetic. A smaller number of real number based sequences make use of Mikko Tommila's apfloat library.
A large number of linear recurrences, generating functions, and tiling sequences are based on code developed by Georg Fischer.
Certain parts of the nauty package for computing automorphism groups of graphs and digraphs were ported to Java. Included here by permission (see associated copyright). For serious work needing this functionality, I would recommend using the C implementations available from nauty.
Similarly, parts of the plantri package for generating planar graphs were ported to Java. Included here by permission (see associated copyright). Again a canonical implementation is available from plantri.
Certain sequences requiring factorization of make use of Tilman Neumann's Java Math Library, larger factorizations are backed by queries to factordb.com.
Certain sequences involving counting positions in chess make use of the Chesspresso library by Bernhard Seybold.
We also recommend having a look at the LODA project.
The tests can be run using ant and the all-tests target of
build.xml. The individual sequence implementations are tested again
the data lines of the corresponding OEIS entries. In order to run the
tests, the stripped.gz is retrieved from the OEIS server and
layed out in a way the tests expect. In addition to testing
individual sequences, the test suite also covers functionality of
shared library code. Running all the tests can take more than an
hour.
This project has benefited immensely and on numerous occasions by other contributors to the OEIS and members of the seqfan mailing list. This ranges from explanations of sequences, detective work, finding papers, vetting edits resulting from this project.
-
H-J. Boehm, The constructive reals as a Java library, ''The Journal of Logic and Algebraic Programming'', 64, (2005), 3-11. [https://doi.org/10.1016/j.jlap.2004.07.002]
-
G. Brinkmann and B. D. McKay, Fast generation of planar graphs (expanded edition). [https://users.cecs.anu.edu.au/~bdm/papers/plantri-full.pdf]
-
G. Brinkmann, S. Greenberg, C. Greenhill, B. D. McKay, R. Thomas and P. Wollan, Generation of simple quadrangulations of the sphere, ''Discrete Mathematics'', 305 (2005) 33-54. [https://users.cecs.anu.edu.au/~bdm/plantri/quad.pdf]
-
A. K. Lenstra, lip: long integer package. Bellcore, 1989. [http://read.pudn.com/downloads103/doc/comm/422470/freelip_1.1/lipdoc.pdf]
-
B. D. McKay and A. Piperno, Practical Graph Isomorphism, II, ''J. Symbolic Computation'', (2013) 60 94-112. [http://dx.doi.org/10.1016/j.jsc.2013.09.003]