NSGA-II Python

Implementation of NSGA-II algorithm in form of a python library.

This implementation can be used to solve multivariate (more than one dimensions) multi-objective optimization problem. The number of objectives and dimensions are not limited. Some critical operators are chosen as: Binary Tournament Selection, Simulated Binary Crossover and Polynomial Mutation. Note that we didn't start everything from scratch but modified the source code from wreszelewski/nsga2. We are very thankful to Wojciech Reszelewski and Kamil Mielnik - authors of this original version. The following items are modified:

• Fix the crowding distance formula.
• Modify some parts of the code to apply to any number of objectives and dimensions.
• Modify the selection operator to Tournament Selection.
• Change the crossover operator to Simulated Binary Crossover.
• Change the mutation operator to Polynomial Mutation.

Usage

1. Class Problem

   Defined in problem.py.

   Using to define a multi-objective problem.

   Arguments:

   • objectives: A list of functions, representing the objective functions.
   • num_of_variables: An integer, representing the number of variables.
   • variables_range: A list of tuples of two elements, representing the lower and upper bound of each respective variables.
   • same_range: A boolean argument, default = False. If true, the range of all variables are the same (this case variables_range has only one element), otherwise each variable has its own range.
   • expand: A boolean argument, default = True. If true, input of functions are treated as list of respective variables (e.x. f(x,y,z)), otherwise they are treated as a vector (e.x. f([x1, x2, x3])).

2. Class Evolution

   Defined in evolution.py.

   Using to run NSGA-II.

   1. Arguments:
      • problem: An object of class Problem.
      • num_of_generations: An integer, default = 1000, representing the number of generations.
      • num_of_individuals: An integer, default = 100, representing the number of individuals, a.k.a the population size.
      • num_of_tour_particips: An integer, default = 2, representing the number of participants in tournament selection operator.
      • tournament_prob: A real number, default = 0.9, representing the probability used in tournament selection.
      • crossover_param: An integer, default = 2, representing the parameter used in simulated binary crossover.
      • mutation_param: An integer, default = 2, representing the paramenter used in polynomial mutation.
   2. Methods:
      • evolve:
        • Arguments: None.
        • Return: List of the best individuals in the last generation.

Example

Examples about SCH problem and KUR problem are showed in sch.py and kur.py.

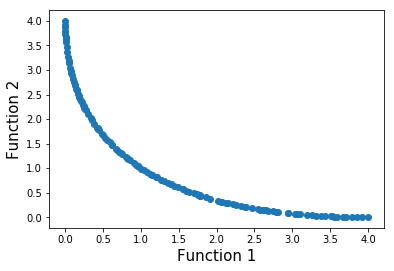
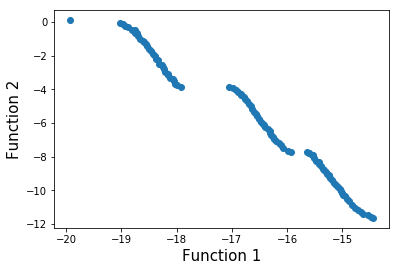
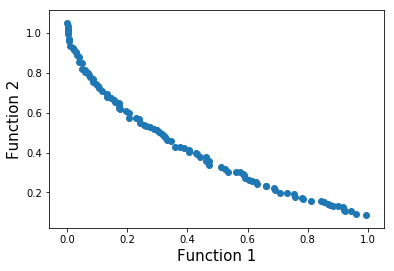
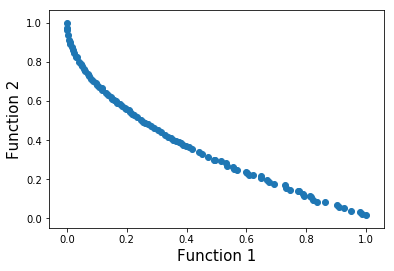
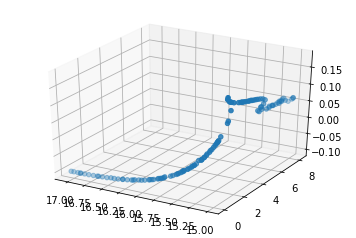
In addition, the results of some popular multi-objective problems is demonstrated as belows:

• SCH
• KUR
• ZDT1
• ZDT4
• VIENNET

Authors

• Pham Ngo Gia Bao, Ho Chi Minh University of Technology
• Tram Loi Quan, Ho Chi Minh University of Technology
• A/Prof. Quan Thanh Tho, Ho Chi Minh University of Technology (advisor)
• A/Prof. Akhil Garg, Shantou University (advisor)

We are very thankful to A/Prof. Tho and A/Prof. Akhil for helping and guiding us to finish this work.