This project is about managing Heap memory. it consists of 10 phases. Each phase discribe some concepts.
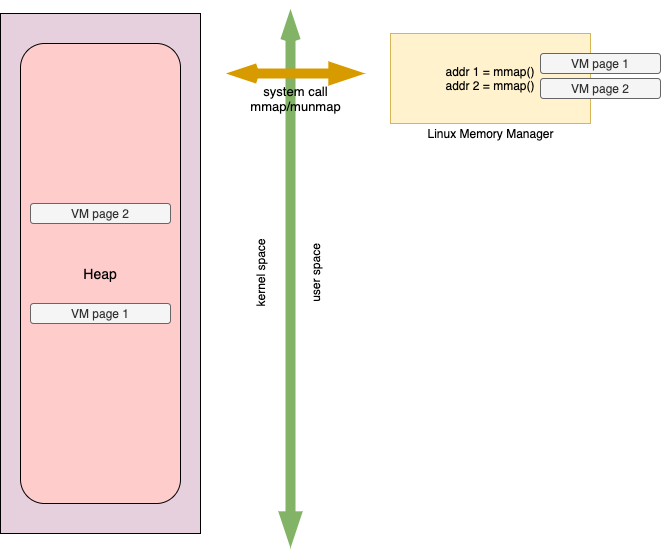
##phase 1 Heap Memory of a process is the continuous part of Virtual Address space of the process from which a process claims and reclaims Memory during runtime (Dynamic Memory allocation). Unlike Stack memory which is reclaimed back upon procedure return automatically, it is the programmer's responsibility to free the dynamic memory after usage. Size of Virtual Memory (VM) page is constant (8192B on most systems). We usually use malloc/calloc to allocate dynamic memory in our program. In fact, malloc/free are linux library functions that uses sbrk/brk system calls to dynamically manage memory. Similarly, another pair of system call called mmap/munmap which are a wrapper for a system call called mmap_pgoff()
based on the above picture:
- Once linux memory manager is assigned the VM complete page from the kernel, LMM will further split VM page to meet the application hunger for memory.
- VM page allocated are need not be contiguous in Heap memory segment of the process as opposed to sbrk behavior.
- Heap memory segment is just a data structure maintained by the kernel for every process, which keeps track of MV pages being used by the LMM.
- Our LMM always request and release memory from the kernel in virtual memory PAGE SIZE granularity.
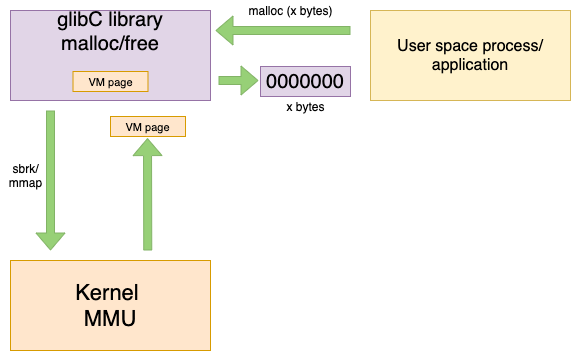
It is important to note that memory allocation/deallocation between user space process and glibC can happen of any size. but page allocation and deallocation between glibC and kernel memory manager (MMU) happens only in units of page sizes. it is because sbrk/mmap system calls are expensive, so that glibC caches the VM page allocated by the kernel MMU and allocates small chunks from it to the process.
##phase 2
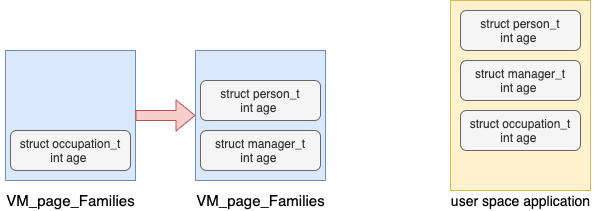
Page Family Registration means the user space application relying on Linux Memory Manager (LMM) during initialization,
tell the LMM the details of the structures application is using.
The user space application should inform the LMM the name and the amounts of bytes for each and every data structures using an API.
page families form a linked list.
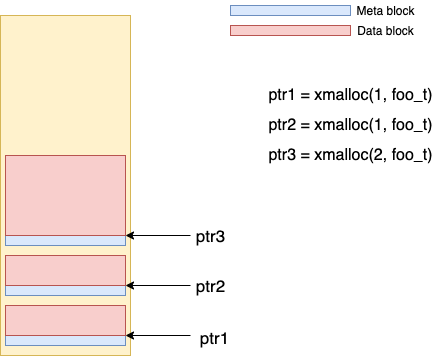
##phase 3 There are two types of blocks VM page context: meta block and data block. These blocks corresponds to user space application memory requests.
Meta block is responsible to store meta information of its data block as well as maintain chains of free and allocated blocks. Application do not know anything about these meta blocks.
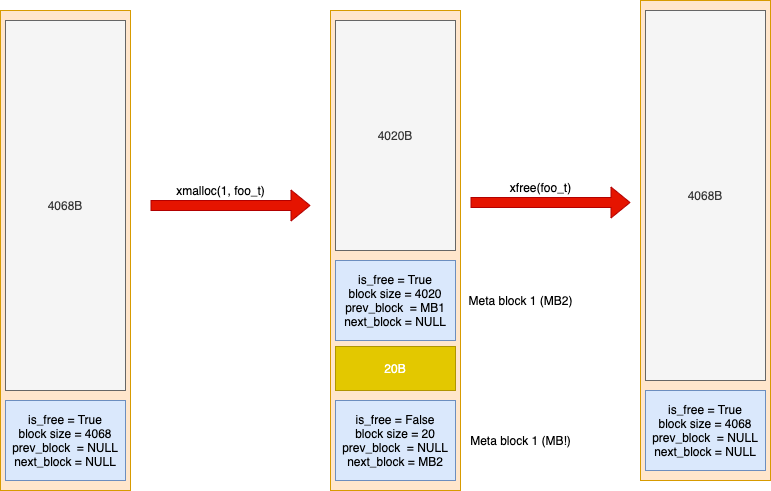
##phase 4 Once the application requests for a VM page, a big data block as well as its meta block is created. Since the size of meta block is 28 bytes, therefore, the size of the first big data block will be 4096 - 28 = 4068 bytes.
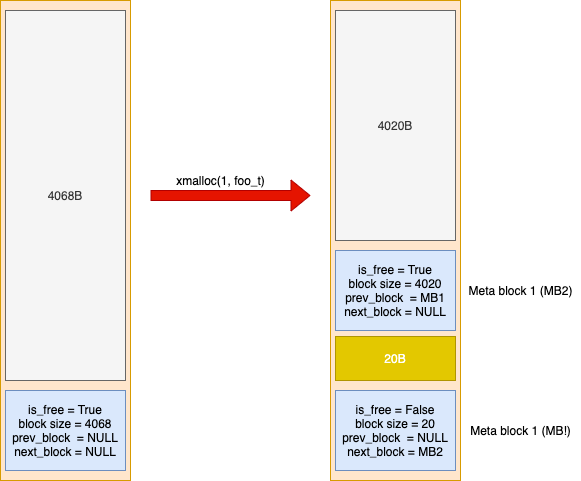
Once the application requests for a memory using xmalloc(1, foo_t), the updated snapshot of the heap memory will be as below:
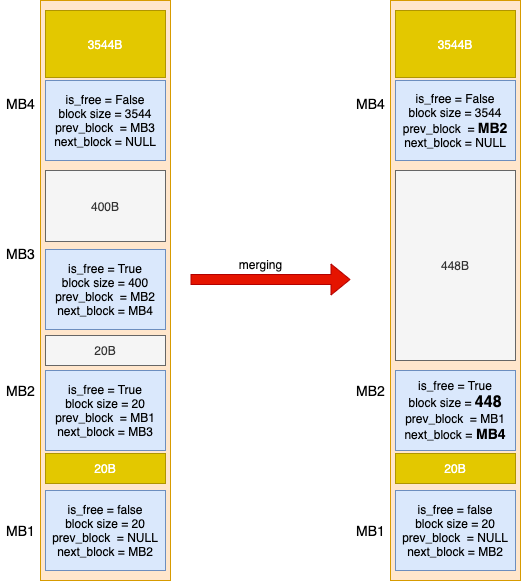
In above picture, the xmalloc API splits the VM page into data blocks. On the other side, xfree API merges consecutive data blocks.
Another scenario that is likely to happen is depicted as below diagram:
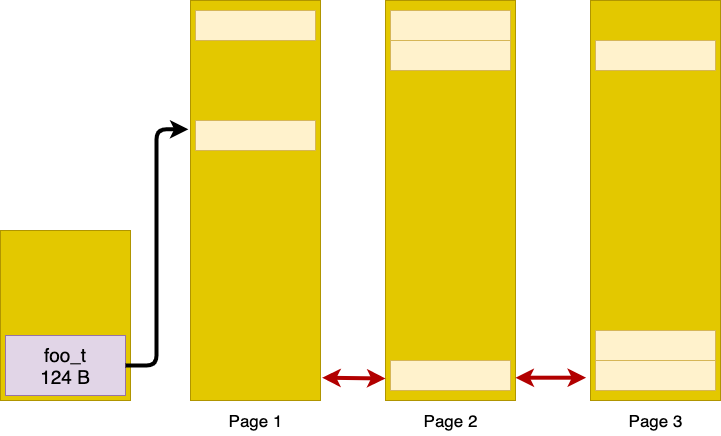
##phase 5 In this step, we are discussing VM page management. Normally, VM pages of an application forms a a doubly linked list.
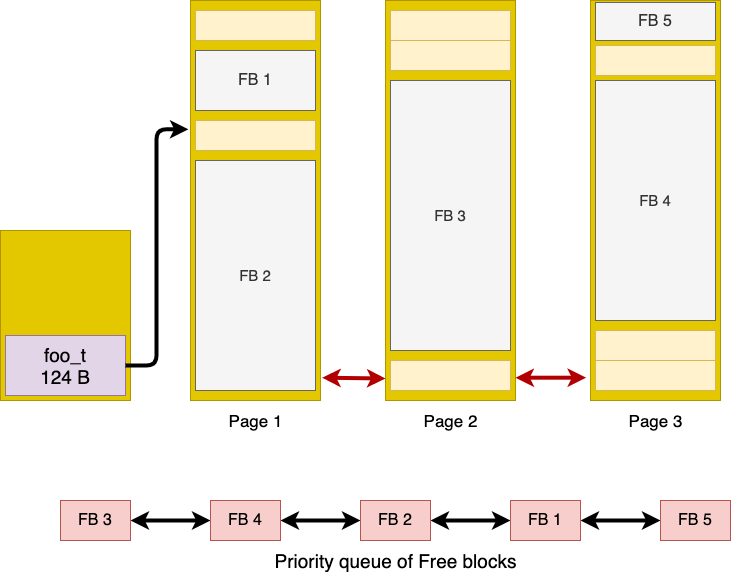
##phase 6 In this phase, we discuss how the linux memory manager assign VM page to a request from the application. Suppose the snapshot of heap memory for the application is like below picture.
At a certain time, the application asks for a VM page. The problem statement here is that how the Linux Memory Manager (LMM) choose a free space to allocate VM for the requested demand. Here, there are three famous algorithm to allocate memory to a request:
- Worst Fit: chooses the largest free space to allocate the request.
- Best Fit: chooses the smallest free space.
- First Fit: chooses the first free space during searching phase.
In this project, we used worst fit technique to allocate memory to the request of the application. The important question arises here is that how to find the biggest free data block across all Data VM pages of a given page family? The answer is each Page Family must maintain a max-priority queue of free data blocks. Note that, the time complexity of Max-Priority queue always will be O(1) whereas in Min-Priority and best fit queue, the time complexity will be O(n). This time complexity can be improved to O(log(n)) if the data structure forms a max-heap.