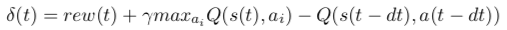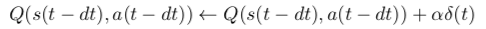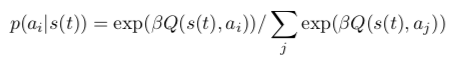TME-NavigationStrategies

IAR - 2023 : le TME est à me rendre à la fin de la séance.

Contexte

Ce TME requiert l'utilisation de la machine virtuelle installée sur les postes fixes de la salle. C'est un complément des cours sur les stratégies multiples de navigation et sur l'apprentissage par renforcement.

Présentation générale

L’objectif de ce TME est de tester plusieurs méthodes de coordination de stratégies de navigation pour un robot doté de deux stratégies simples, en quantifiant leur efficacité dans un environnement où la coopération de ces stratégies est nécessaire.

Deux stratégies de navigation sont pré-programmées :

• Un suivi de mur (wallFollower.py) qui maintient le robot à distance des murs (trop près, il s'en éloigne, trop loin il s'en rapproche), tourne sur lui-même à la recherche d'un mur s'il n'y en a pas à proximité, ou s'il a un obstacle devant lui.
• Une approche de balise (radarGuidance.py) qui oriente le robot vers une balise dont la direction est fournie, mais qui n'évite pas les obstacles.

Elles sont testables de manière isolée en lançant python wallFollower.py et python radarGuidance.py. La coordination des deux stratégies est à coder dans strategyGating.py, qui contient déjà le code permettant de lancer la simulation, de récupérer les données des senseurs, de les transformer en un identifiant d'état (voir plus loin), de téléporter le robot lorsqu'il arrive au but (et de le récompenser), de le punir lorsqu'il approche trop d'un mur, et de répéter les opérations jusqu'à l'obtention de 40 récompenses.

Le codage proprement-dit de ce TME correspond à, maximum, 40 lignes de python. Il faut faire du code propre et qui marche mais ça n'est pas le cœur du travail : il s'agit surtout d'essayer d'avoir une approche scientifique par rapport à la question posée. A savoir : mesurer les phénomènes avec, autant que possible, suffisament de répétitions pour en extraire la tendance générale et la dispersion autour de cette tendance, les quantifier afin de pouvoir effectuer des comparaisons, représenter les données obtenues de manière lisible, analyser et commenter ces résultats.

Informations techniques

Vous allez devoir ajouter du code dans la fonction strategyGating du fichier strategyGating.py pour coder les méthodes d'arbitrage proposées en exercice, et aussi probablement du code pour enregistrer des données en fin d'expérience, à la fin de la fonction main de ce même fichier. Chaque méthode d'abitrage doit, au final, indiquer le choix de l'une ou l'autre des stratégies de navigation en affectant la variable choice avec 0 (activation du suivi de mur) ou 1 (activation de l'approche de balise).

Lorsqu'une expérience est menée à terme (jusqu'à atteindre nbTrials), la durée de chaque essai est enregistrée dans un fichier de la forme log/time-TrialDuration-method.txt (pensez à créer un répertoire log/).

Description du problème

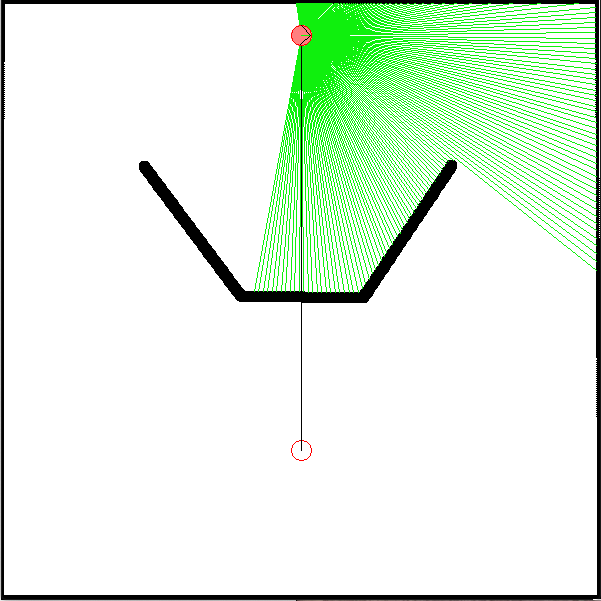
L’environnement utilisé est composé d’une arène carrée (600x600 pixels) comprenant un obstacle, et un but. Ce but est de type goal dans fastsim, ce qui veut dire qu’il s’agit d’une balise dont la direction peut être détectée par un senseur de type radar, même à travers les murs.

Le robot est équipé des capteurs suivants :

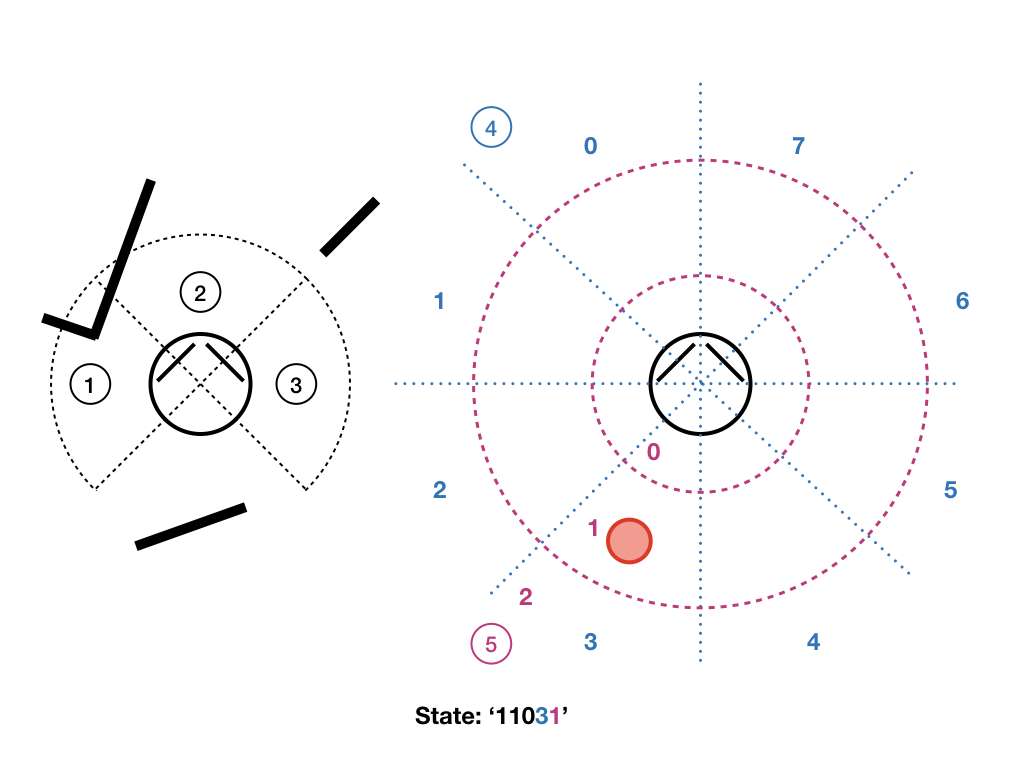
• un télémètre laser de 200 degrés d’ouverture, fournissant une mesure de distance tous les degrés,
• des détecteurs de contact droite et gauche,
• un radar capable de détecter la direction du but dans l’un des 8 secteurs autour du robot,
• un capteur grossier de distance de la balise (0 : proche, 1 : moyenne, 2 : éloignée) est simulé à partir de la position du robot produite par le simulateur, elle est utilisée dans la définition d'état pour l'apprentissage.

Le robot démarre toujours la simulation à la position (300,35).

L’obstacle en forme de U fait qu’un robot utilisant la stratégie d’approche de balise seule va y rester coincé. De la même façon, la stratégie de suivi de mur va soit faire tourner le robot autour de l’arène, soit autour de l’obstacle, sans lui permettre d’atteindre le but. Il va donc être nécessaire de coordonner l’usage de ces deux stratégies afin de résoudre la tâche dans un temps raisonnable.

strategyGating.py est conçu pour que, par défaut, lorsque le robot atteint le but, il soit téléporté à son point de départ. Cette téléportation marque la fin d’un « essai » (trial), le programme s’arrête de lui-même lorsque ce nombre d’essais atteint la valeur nbTrials (40), que vous pouvez donc modifier selon vos besoins. Chaque fois que le robot atteint le but la variable de récompense rew passe à 1 et chaque fois qu’il percute un mur, elle passe à -1. C’est à la méthode d’arbitrage (que vous allez programmer) de remettre cette valeur à 0 lorsque l’information a été traitée.

Exercices

Prévoyez de m’envoyer par mail à la fin du TME votre code de strategyGating.py, les fichiers de log contenant les informations demandées (durées des essais, Q valeurs), ainsi qu'un pdf de vos réponses aux questions, en me rappelant la composition de votre binôme.

1. Vous pouvez constater en lançant un arbitrage de type random qu’un choix uniforme à chaque pas de temps de l’une des deux stratégies n’a pratiquement aucune chance de sortir le robot du cul-de-sac. Ecrivez une première méthode d’arbitrage randomPersist choisissant l’une des deux stratégies avec la même probabilité, mais persistant dans son choix pendant deux secondes. Cette stabilité accrue dans les choix devrait permettre au robot d’avoir une réelle chance de sortir du cul-de-sac.

2. Effectuez 20 essais avec cette nouvelle stratégie, gardez de côté le fichier XXX-TrialDurations-YYY qui contient le temps nécessaire à chaque essai pour atteindre le but. Calculez la médiane, les premier et troisième quartiles de ces temps. Ces données vont nous servir de référence: toute méthode intelligente devra essayer de faire mieux que cette approche aveugle. Vous pouvez, pour cela, utiliser la fonction « percentile » de numpy.

Pro-tip : Pendant que ça tourne, plutôt que de vous laisser hypnotiser par le robot qui bouge, attaquez la question suivante : vous avez un temps limité...

3. Implémentez une méthode d'arbitrage qlearning similaire à celle utilisée par (Dollé et al., 2010) : elle utilise un algorithme de Q Learning pour apprendre, essai après essai, quelle est la meilleure stratégie à choisir en fonction de l’état du monde.

Définition des états : On travaille ici avec une approche tabulaire, les états sont discrets, ils ont un identifiant qui est une chaîne de caractère construite de la manière suivante : les trois premiers caractères (0 ou 1) indiquent s'il y a un mur à proximité à gauche, au milieu, à droite ; le caractère suivant, entre 0 et 7, indique la direction de la balise ; le dernier (0, 1 ou 2) indique si la balise est proche (<125 pixels), moyennement éloignée (<250 pixels), ou lointaine (>= 250 pixels). Ces états sont déjà construits (par la fonction buildStateFromSensors), l'état courant est lisible dans S_t, l'état précédent dans S_tm1.

Q-Learning : Il vous faut créer et mettre à jour la valeur Q(s,a) des couples (état,action) rencontrés, et l'utiliser chaque fois que nécessaire pour choisir la prochaine stratégie de navigation active. Pour cela, il faut calculer à chaque pas de temps l'erreur de prédiction de récompense :

Puis mettre à jour la Q-valeur correspondant à la dernière action effectuée :

Le choix de l'action est alors effectué en effectuant un tirage dans la distribution de probabilité résultant d'un softmax sur les Q-valeurs de l'état courant:

Dans un premier temps, utilisez les paramètres : alpha=0.4, beta=4, gamma=0.95.

Dans notre cas particulier, les actions sont continues, prennent un temps indéfini. Faire des mises à jour à chaque pas de temps n'a pas beaucoup de sens : en 10 millisecondes, l'état sensoriel risque de peu changer, et le signal de valeur risque de se diluer très vite, à moins de prendre un gamma très très proche de 1. On pourrait ne faire des mises à jour de Q-Learning que lorsque l'état change, ou qu'un signal de récompense arrive, mais dans ce cas là, on pourrait rester indéfiniment coincé dans un état si l'action choisie ne permet pas d'en sortir. Pour contourner ces problèmes, on va ajouter une limite de temps (timeout) maximale de 2 secondes.

Il vous est donc demandé de faire fonctionner l'algorithme de la manière suivante :

• faire une mise à jour de Q(s,a) lorsque l'état vient de changer, lorsqu'on a fait un choix à la boucle précédente, ou lorsque la récompense est non-nulle.
• choisir une nouvelle action lorsque l'état vient de changer, lorsque la récompense est non-nulle ou lorsqu'il n'y a pas eu de changement de choix depuis 2 secondes.

4. Pour caracterister le comportement de ce Q-Learning, sauvegardez les Q-valeurs obtenues à la fin du 40e essai.

5. Pour estimer l'efficacité de ce Q-Learning, répétez 4 à 10 fois (selon le temps disponible) des expériences de 40 essais successifs, et pendant que ça tourne, passez à l'étape 6.

6. Dans les Q-valeurs sauvegardées à l'étape 4, quelles sont celles des états 00002 et 00072 ? 00000 et 00070 ? 11101 et 11171 ? Ces valeurs, pour chacune des deux stratégies, vous semblent-elles logiques ?

7. Une fois les données de l'étape 5 obtenues :

• produire une figure représentant les courbes de durée de chaque essai pour les runs réalisés. La commenter.
• mesurez la médiane et les quartiles de la durée des essais sur les 10 premiers essais de tous les runs cummulés, puis sur les 10 derniers. Observez-vous une amélioration des performances ? Comment cette mesure sur les 10 derniers essais se compare-t-elle à celle réalisée à l'étape 2 ? Le Q-Learning est il meilleur après apprentissage ?

N'oubliez pas de m'envoyer les fichiers de log, votre code de strategyGating.py et un pdf contenant vos réponses aux questions et vos figures.