Background

Cellular automata are a computational model which can been used to model complex systems. They can be applied in areas like biological modeling, solving partial differential equations, and much more. As such, determining how to best execute the automata on large scale distributed systems is a matter of increasing importance in the present day. Optimizing algorithmic implementations will help increase performance, as well as help overcome memory limitations for any initial conditions of the automata.

More specifically, we seek to optimize parallel execution of automata that use the Moore neighborhood for implementation, where rules are based on all directly adjacent cells, including diagonally. We will compare two different programs for this, one which uses a row-wise partitioning scheme and another which uses grid wise [@cellauto] (shown below in Figure [fig:parts]{reference-type="ref" reference="fig:parts"}). We hope to see which of these approaches results in the most efficient communication between processes. We also hope to time view-based I/O [@io] algorithms for each of these, and see what fraction of the runtime is affected by I/O.

{#fig:sub1}

{#fig:sub2}

Each of these methods have the same communication requirements. That is, each must send the outermost edges of their partitions to each of their neighbors, and likewise receive them, in order to have enough information to update their own cells on the outermost edges. The only difference lies in which portion of the cell grid each process has.

Predictions

To determine the point at which one of these schemes beats the other, we may use the postal model. For the row-wise partition, we have that each process must send 2 message, one for the top row and one for the bottom row. Each of these rows have a total of $n$ cells, so the time required for communication must be:

$$T = 2 \alpha + (2n)\beta$$

On the other hand, the grid-wise partitioning sends a total of 8 messages (4 for the sides, 4 for the corners), and the length of each side is $n\sqrt{p}$. So we have:

$$T = 8\alpha + \left(4 + 4\frac{n}{\sqrt{p}}\right)\beta$$

Given that $\alpha$ is usually much larger than $\beta$, for small input sizes the first approach will be faster than the second. However, as we increase the input size, it will be outperformed for larger values of $p$.

Implementation

We used point-to-point communication to implement both of the algorithms. [@repo] Communication for the row-wise algorithm is as follows:

send top row of state to up send bottom row of state to down receive from down into up_buf receive from up into down_buf receive from down into up_buf receive from up into down_buf send top row of state to up send bottom row of state to down

(The update state function uses the state and the buffers to get the neighbors of each cell, then looks in the rule table for the expected new state)

As for I/O, each version was implemented using a higher level view-based algorithm in order to read in the initial conditions of the automaton (that is, an $n \times n$ matrix of integers, where the element at row $i$ and column $j$ is the initial state of the corresponding cell.

create MPI datatype $t$ describing sub-portion of file open file set file view to $t$ perform collective read or write

The only change in the algorithm between the two partition versions lies in the datatype. For row-wise, we use MPI_Type_Contiguous, and for grid wise we instead use MPI_Type_create_subarray to create an $n \times n$ subset of the original matrix.

For the grid wise version of the program, the communication works as such:

make MPI_Isend request for top row make MPI_Isend request for upper right corner $\vdots$ make MPI_Isend request for upper left corner receive top row $\vdots$ receive upper left corner

The requests are done using datatypes to avoid the extra computation cost of copying the columns into the buffers before sending.

Results

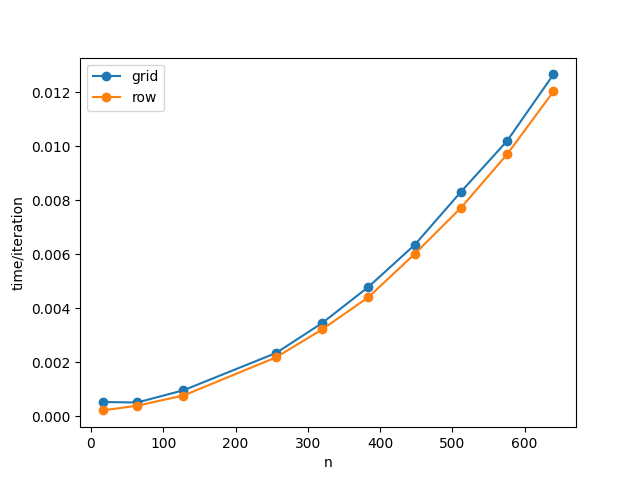
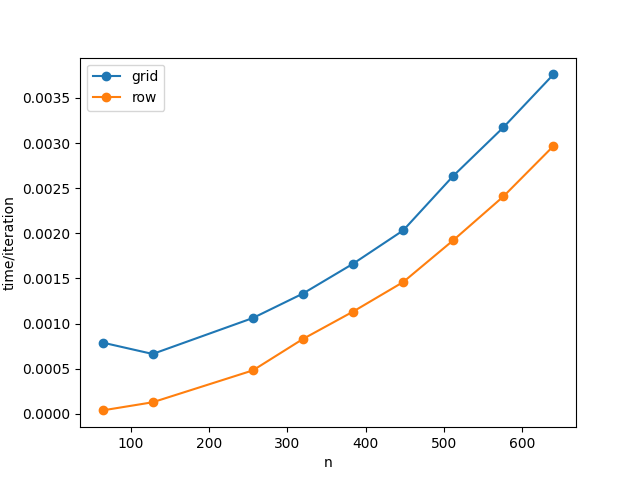
To test our hypothesis, we ran our implementation on wheeler, and tested it over several multiples of 64 for the input sizes, one time using 16 processe and another using 64. We timed both communication and execution for 100 iterations of Conway's Game of Life [@life] over randomly generated initial states, and divided by 100 to get an approximation of time per iteration. Below in figure [fig:comcosts]{reference-type="ref" reference="fig:comcosts"} are the results for both numbers of processes.

{#fig:sub1}

{#fig:sub2}

Our results actually ended up being contrary to what we theorized before. As can be seen, the row version is faster than the grid version, as if by a constant addition. There are a number of different possible reasons for this, all based on things that were not accounted for in the model. For one, the additional time for queue searching for each of the MPI_Recv calls was not included, as there are more receives in the grid version. It is also possible that the row version is more topology respecting than the grid version. Lastly, there is an additional computation cost in the grid version from having to check more conditions when deciding which array to retrieve the cell from, whereas for the other version we just decide between the main grid, the top buffer, and the bottom buffer.

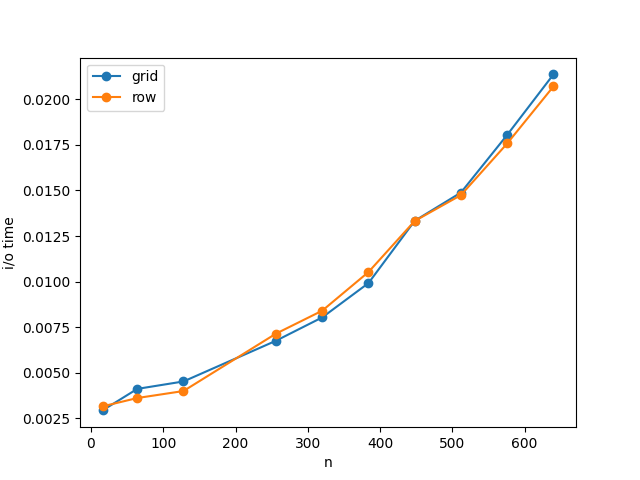
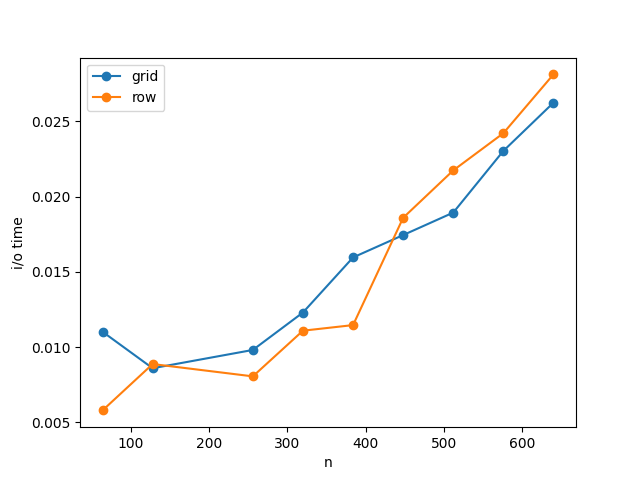
There were also timings made for reading in the initial state for both of these program counts, shown in figure [fig:iocosts]{reference-type="ref" reference="fig:iocosts"}. It seems that, for lower process counts,t he I/O performance of both versions is roughly the same. When there are more processes, however, the grid-based version out-performs the other.

{#fig:sub1}

{#fig:sub2}

Conclusion + Future Work

Overall, we did not see the results we were looking for, namely that the grid partitioning is more efficient than the row partitioning. Instead we got the complete opposite. This could perhaps tell us that, for input matrix sizes that aren't extremely large, the benefit of the grid partitioning isn't obvious, mostly because the input matrix size scales quadratically as $n$ increases while the communication requirements only scale linearly. There are still many possible optimizations that could be made in the future to make the one method approach the other more quickly.

In the future, one possible optimization that could be made is to instead store the intial state of the automaton as a sparse array of integers, at least for cases where most of the cells are the same (as was the case in most initial configurations for Conway's GOL). It would also be beneficial to look into possible optimizations using one-sided communication, and perhaps to further parallelize the execution using MPI + OpenMP.

9 A. Giordano, A. De Rango, D. D'Ambrosio, R. Rongo and W. Spataro, "Strategies for Parallel Execution of Cellular Automata in Distributed Memory Architectures," 2019 27th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP), 2019, pp. 406-413, doi: 10.1109/EMPDP.2019.8671639.

Blas, Javier Garc, et al. "View-Based Collective I/O for MPI-IO." 2008 Eighth IEEE International Symposium on Cluster Computing and the Grid (CCGRID), 2008, https://doi.org/10.1109/ccgrid.2008.85.

"Conway's Game of Life." Wikipedia, Wikimedia Foundation, 28 Nov. 2022, https://en.wikipedia.org/wiki/Conway%27s\_Game\_of\_Life #/media/File:Game_of_life_loaf.svg

Gardner, Martin. " The Fantastic Combinations of John Conway's New Solitaire Game 'Life.'" Scientific American, Oct. 1970, pp. 120--123. https://github.com/christopherjmedlin/cs442-final-project