EUREQA

Run Code

python3 -X pycache_prefix=bytecodes codes/eureqa.py 

Description of the problem:

You have a real-world phenomenon, and you want to know what the function that describes its behavior.

Project description:

A simpler version of the Eureqa program is requested. A data set of a real world phenomenon is given. Candidate functions to approximate the data are of the form h(x) = f(x) + g(x), where both f and g, may be:

0. real constants: k

1. polynomials of degree less than or equal to 4

2. = k1 e^(k2*x)

3. = k1 sen(k2*x)

4. = k1 cos(k2*x)

The program must use the genetic algorithm technique to find a function h that describe this phenomenon.

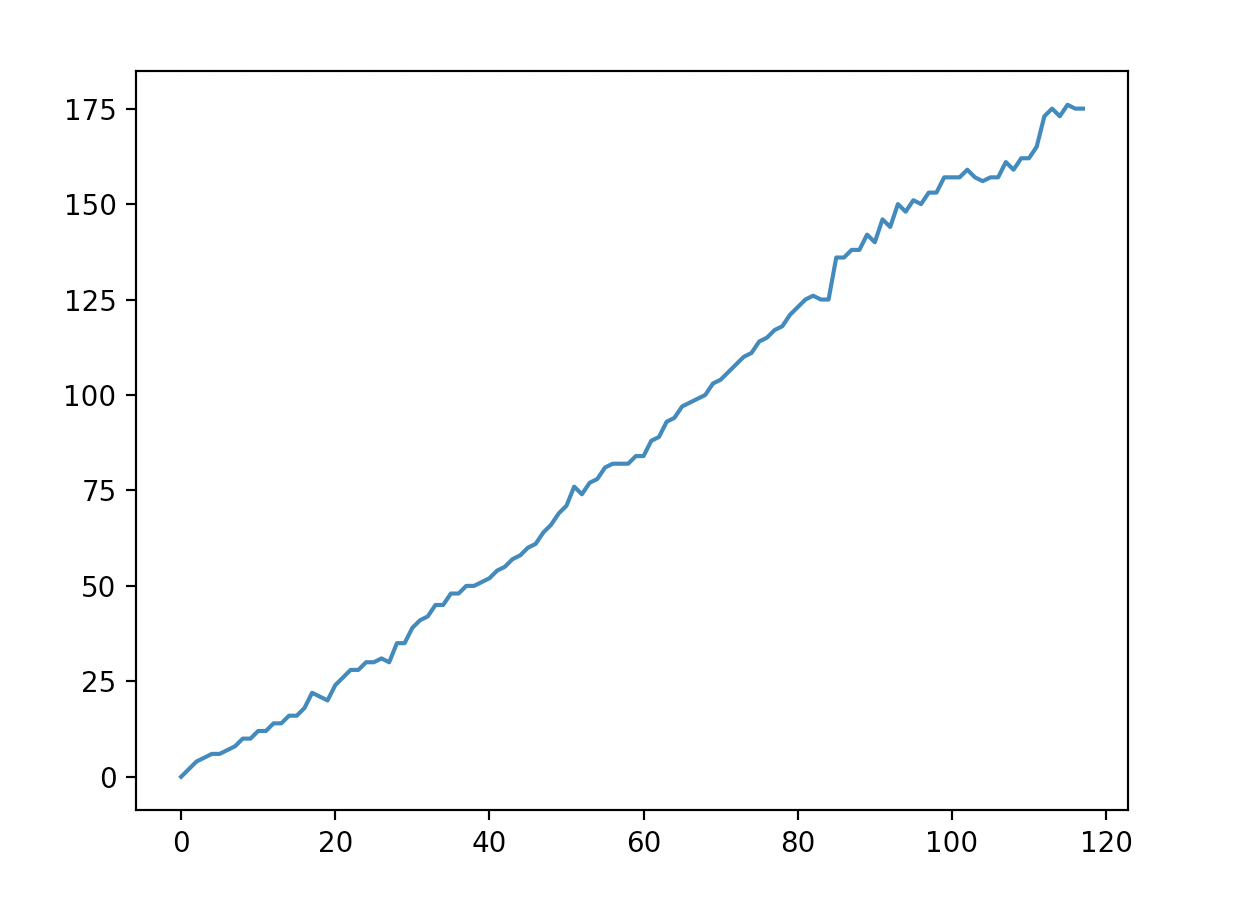
x	f(x)	x	f(x)	x	f(x)	x	f(x)
1	0	2	2	3	4	4	5
5	6	6	6	7	7	8	8
9	10	10	10	11	12	12	12
13	14	14	14	15	16	16	16
17	18	18	22	19	21	20	20
21	24	22	26	23	28	24	28
25	30	26	30	27	31	28	30
29	35	30	35	31	39	32	41
33	42	34	45	35	45	36	48
37	48	38	50	39	50	40	51
41	52	42	54	43	55	44	57
45	58	46	60	47	61	48	64
49	66	50	69	51	71	52	76
53	74	54	77	55	78	56	81
57	82	58	82	59	82	60	84
61	84	62	88	63	89	64	93
65	94	66	97	67	98	68	99
69	100	70	103	71	104	72	106
73	108	74	110	75	111	76	114
77	115	78	117	79	118	80	121
81	123	82	125	83	126	84	125
85	125	86	136	87	136	88	138
89	138	90	142	91	140	92	146
93	144	94	150	95	148	96	151
97	150	98	153	99	153	100	157
101	157	102	157	103	159	104	157
105	156	106	157	107	157	108	161
109	159	110	162	111	162	112	165
113	173	114	175	115	173	116	176
117	175	118	175

Gene

f_f : Function f(x)
f_g : Function g(x)
c : Constant value
k1_f : Constant k1 of f(x)
k2_f : Constant k2 of f(x)
k1_g : Constant k1 of g(x)
k2_g : Constant k2 of g(x)

Chromosomes

[f_f, f_g, cf, cg, k1_f, k2_f, k1_g, k2_g]

To Find more information, please go to :

https://www.tusclases.co.cr/blog/algoritmo-genetico-schedule-optimization-python