Diamond_Square

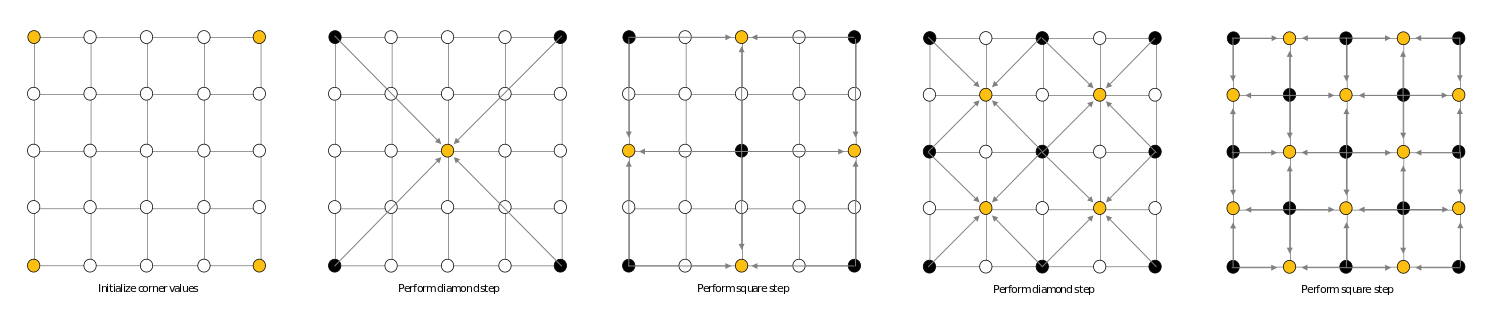
Implementation of Diamond Square algorithm.

Setup instructions

This project uses a Makefile in which several targets are provided for ease of use.

For a minimal setup run make setup to install requirements:

• matplotlib==1.5.3
• numpy==1.11.2)

Running make run will run the code.

Diamond-Square Algorithm

Overview

Initial Conditions

Input values are the G_SIZE which defines grid size according to (2^G_SIZE + 1) & G_MAX_RND for minimum and maximum random number. G_SIZE serves as a measure of level which is looped 0 -> G_SIZE. where 0 starts with large shapes and G_SIZE represents the smallest shapes according to below image. Source.

The function _rnjesus takes single input value N and generates a random value between -N -> +N.

The grid is seeded with 4 random values in range -G_MAX_RND -> +G_MAX_RND. Each point is computed by taking the average and adding a random number to it. This random number is reduced at each level see image according to G_SIZE/(level+1). This is a crude implementation but allows for sufficiently random terrain & sufficient smoothness.

Square Step

Square step (so called as reference points form a square) is computed simply. C is the computed point using marked points below.

  NW          NE
        C
  SW          SE

Diamond Step

Diamond step (so called a reference points form a diamond) requires a wrapping if the index are minimum and maximum values. The loop also has some redundancies as two points will be looked at twice however once a point has been assigned a value it will not be recomputed.

N,W,S,E are computed using surrounding reference points. NN, WW, EE, SS are points which wrap if outside index range.

              NN
        NW    N     NE
  WW    W     C     E     EE
        SW    S     SE
              SS

Sample images

Three Dimensional

Two Dimensional