radgrad

---

radgrad (rad = reverse-mode automatic differentiation) is an educational implementation of automatic differentiation on top of a Numpy wrapper. It is a (very) simplified clone of Autograd.

Here's a basic example:

import radgrad.numpy_wrapper as np
from radgrad import grad

def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))

print(tanh(1.0))
dtanh_dx = grad(tanh)
print(dtanh_dx(1.0))

grad is a higher-order function. It takes a function expressing a mathematical computation using Numpy, and transforms it into a function that computes the derivative of this computation. In the code above, the call tanh(1.0) evaluates the value of the tanh function at 1.0; the call dtanh_dx(1.0) evaluates the derivative of the tanh function with respect to its inputs at 1.0.

To understand how radgrad works, start by reading this blog post. Then, read through radgrad's code and play with the examples. The code is heavily commented to explain what's going on.

To make the learning journey easier, this project is split into two parts:

• Part 1: implements the simplest AD mechanism possible, with support for first order derivatives only.
• Part 2: builds on top of part 1 to implement higher-order derivatives.

The code of parts 1 and 2 is almost identical; I recommend starting with Part 1, and once you understand how it works, run a recursive diff (e.g. meld part1-basic/ part2-higher-order/) to get a feeling for the deltas. Read more on higher-order derivatives in radgrad below.

Tracing AD approach

radgrad implements tracing AD; when grad(f) is invoked, there's no static analysis of f's code going on. Instead, grad wraps all the arguments passed into f with special Box types that keep track of the operations performed on them (using a mix of operator overloading and specially wrapped Numpy primitives). This is used to construct an implicit computational graph (implicit in the sense that the user isn't even aware of it) on which the reverse mode AD process can be run.

This lets us calculate derivatives of code that contains Python control flow; here's an example from examples/taylor-sin.py:

from radgrad import grad
import math

def taylor_sin(x):
    ans = term = x
    for i in range(0, 20):
        term = -term * x * x / ((2 * i + 3) * (2 * i + 2))
        ans = ans + term
    return ans

dsin_dx = grad(taylor_sin)

for x in ["0.0", "math.pi / 4", "math.pi / 2", "math.pi"]:
    xname, xval = x, eval(x)
    print(f"sin({xname}) = {taylor_sin(xval):.3}")
    print(f"dsin_dx({xname}) = {dsin_dx(xval)[0]:.3}")

taylor_sin computes a Taylor series approximation to sin. Note how it uses a Python loop; grad(taylor_sin) still works, even though it's not clear what the derivative of a Python loop even means! In reality, the tracing approach ensures that the loop is unrolled in the computational graph - it only sees the actual path taken by a specific invocation.

Running the code

I find it easiest to run this code using uv. For example:

$ cd part1-basic
$ PYTHONPATH=. uv run examples/tanh.py

Some examples plot graphs using matplotlib. If you want to see the plots, ask uv to include matplotlib in the dependencies, as follows:

$ cd part2-higher-order
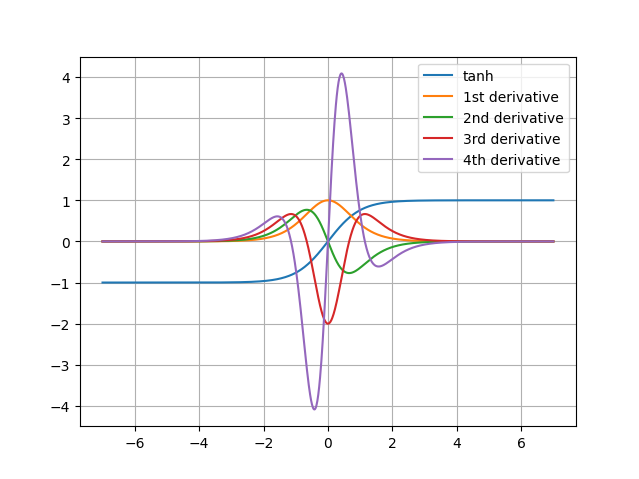
$ PYTHONPATH=. uv run --with matplotlib examples/tanh.py

This produces a plot of several levels of derivatives of the tanh function:

Higher-order derivatives in Part 2

Some notes of how Part 2 works, and what's different from Part 1.

The key insight is that the derivative calculation is a sequence of primitives and operators, just like the original computation; therefore, if we trace the derivative calculation, we can also find the derivative of the derivative. The changes from Part 1 to Part 2 make this possible, in two steps.

The simpler step to explain is making sure our VJP functions are defined in terms of traced primitives rather than original Numpy primitives, e.g:

add_vjp_rule(_np.sin, lambda x: (sin(x), lambda g: [cos(x) * g]))

Note that the gradient now uses cos(x) * g rather than _np.cos(x) * g. cos is our wrapped primitive, so it supports tracing.

The more complicated step is ensuring that recursive invocations of grad compose properly and don't interfere with each other, since there are multiple levels of Boxes involved. This is done by adding a level for each box, with the level becoming automatically higher for every additional derivative.

To understand how this works, consider this simple example¹:

import radgrad.numpy_wrapper as np
from radgrad import grad1

def f(x):
    return x + np.sin(x)

df_dx = grad1(f)
print(df_dx(0.5))

What happens when df_dx(0.5) is invoked?

A Box is created for 0.5; this box has an empty node with no predecessors, since it's an argument ("root" node). Then f is called with the Box as the argument. Python evaluates the expression inside f.

It starts with np.sin(x), which calls our wrapped sin primitive. Since x is already a box, there's no need to box it again. The VJP rule for sin is invoked, calculates the actual value np.sin(0.5) and returns a VJP function that will calculate np.cos(0.5) * g when called with g. Finally, the output is Boxed with a Node that has the argument x as the predecessor.

The overloaded + operates similarly, and we end up with something like the following computational graph built out of Nodes (the arrows point to predecessor nodes):

graph TD;
    ADD-->SIN;
    ADD-->X;
    SIN-->X;

Loading

Then backprop is invoked on this graph with the ADD node as the starting point. It calls the VJP function of +, and then the VJP function of sin, which itself calculates np.cos(0.5) * g.

But note that we said we're replacing np.cos by cos in the VJP functions of Part 2. So this backpropagation through the computational graph is itself a Python computation composed of a sequence of wrapped operations, meaning it can build its own computational graph for the second derivative and so on.

This is exactly how higher-order derivatives work in radgrad. The only issue to resolve is that when backpropagation runs, some of the values involved may already be Boxes. For example, in the VJP function of sin we have cos(x) * g where cos(x) is a Box (because x is), while g is not nominally a box. When the * operator invokes a wrapped computation with arguments cos(x) and g, it doesn't Box values that are already Boxes, but this is a mistake, because cos(x) would have a Node with predecessors relevant to the first derivative calculation, not the second. Recall that the computational graph is built while the computation is running; if something is already a box, we should not interefere with it because it contains critical information for building the computational graph of the computation.

The solution is to add the concept of a "box level".

@dataclass
class Box:
    """Box for AD tracing.

    Boxes wrap values and associate them with a Node in the computation graph.
    level specifies the tracing level of the box - higher levels are used for
    higher-order gradients.
    """

    value: typing.Any
    node: Node
    level: int = 0

Each time grad is invoked, it increments a (global) box level, and decrements it when the derivative calculation is fully done. For nested invocations of grad as in grad1(grad1(f)), the innermost grad1 (calculating the first derivative) will create boxes with level 1, while the outer grad1 (calculating the second derivative) with level 2. wrap_primitive is adjusted to box all arguments at the highest level of any argument - to ensure that existing lower-level Boxes are put into other Boxes (because the computation arguments will be incoming at the highest box level). This prevents mixing up computational graphs between the different orders of derivatives.

This technique is borrowed from Autograd. The JAX framework generalizes it to a nesting of different "interpreters" that all compose (e.g. grad and other things like vmap). See the autodidax doc for more details on this.

Footnotes

1. Part 2 also adds a grad1 helper - it just wraps grad to return a single derivative instead of a list; this results in nicer code when we want to compute higher-order derivatives of functions with a single argument, e.g. d3y = grad1(grad1(grad1(tanh)))(x). ↩