2D-Robot-Evolution

A Java framework for experimenting with the evolutionary optimization of 2D simulated robotic agents.

Based mainly on JGEA and 2D-MR-Sim.

Installation

Dependencies

This software requires JDK 17 and maven: if you are using a Unix based system, you can install both easily using sdkman.

This software also depends on the following other dependencies (JGEA, 2D-MR-Sim, JNB, JSDynSys), that will be fetched automatically by maven.

In case you want to use this project inside your project, add this to your pom.xml:

<dependency>
    <groupId>io.github.ericmedvet</groupId>
    <artifactId>robotevo2d.main</artifactId>
    <version>1.5.0</version>
</dependency>

Clone and build

You can clone this project and build it with:

git clone https://github.com/ericmedvet/2d-robot-evolution.git
cd 2d-robot-evolution
mvn clean package

At this point, if everything worked smoothly, you should be able to run a first short evolutionary optimization (assume you are in the parent directory of the 2d-robot-evolution one that has been created after the last clone; this is suggested for real runs, so that you don't pollute your git branch with outcome files):

java -jar 2d-robot-evolution/io.github.ericmedvet.robotevo2d.main/target/robotevo2d.main-1.5.0-jar-with-dependencies.jar -f 2d-robot-evolution/src/main/resources/exp-examples/locomotion-centralized-vsr.txt

For Windows, it might be possible that by using the command above from the standard terminal you see garbage text output. It happens because Windows is not able to manage the extended charset needed to encode the colored textual UI. You can use javaw instead of java for launching the Starter class to circumvent the problem.

Usage

In a nutshell

An experiment can be started by invoking:

java -jar 2d-robot-evolution/io.github.ericmedvet.robotevo2d.main/target/robotevo2d.main-1.5.0-jar-with-dependencies.jar --expFile <exp-file> --nOfThreads <nt>

where <exp-file> is the path to a file with an experiment description and <nt> is the number of threads to be used for running the experiment.

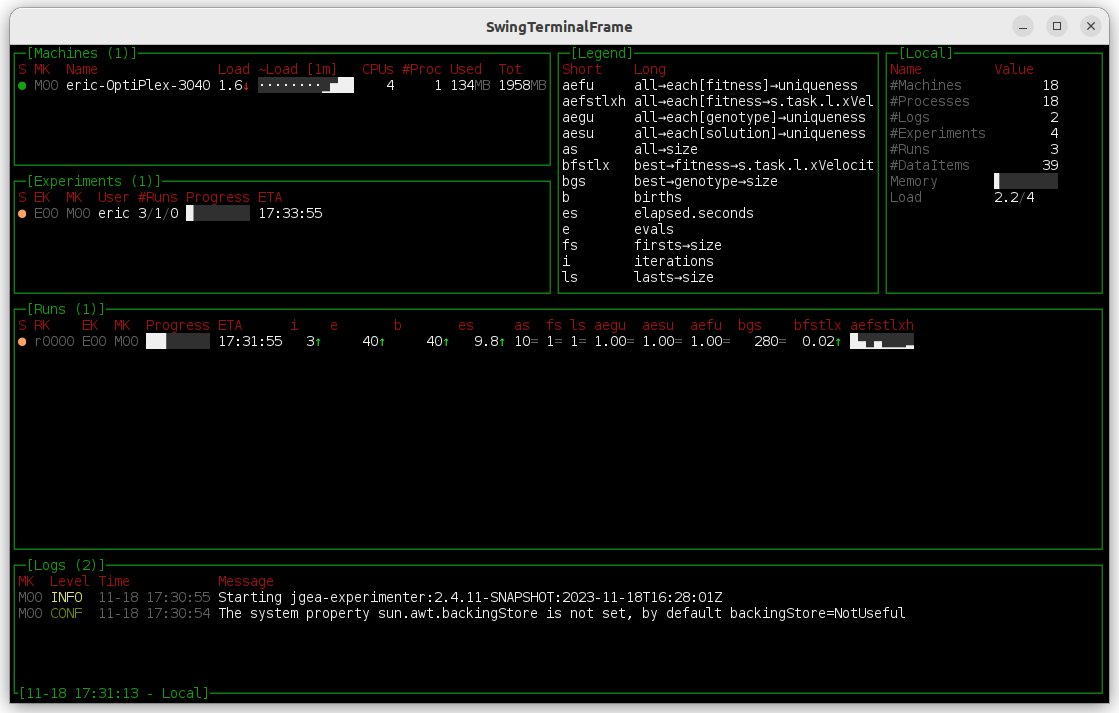
Once started, Starter shows a text-based UI giving information about the overall progress of the experiment, the current run, logs, and resources usage. Starter may be stopped (before conclusion) with Ctrl + C.

For the number of threads <nt>, it is suggested to use a number $n$ lower or equal to the number of cores on the machine you run the experiment on. The actual degree of concurrency will depend on $n$ and on the evolutionary algorithm being used: e.g., a GA with a population of npop = 30 will do at most $\min(30,n)$ fitness evaluations at the same time.

You can have an overview on the other (few) parameters of Starter with:

java -jar 2d-robot-evolution/io.github.ericmedvet.robotevo2d.main/target/robotevo2d.main-1.5.0-jar-with-dependencies.jar --help

One parameter that may be handy is --checkExpFile, or just -c, that can be used to perform a syntactical check on the experiment description file, without actually doing the experiment.

The experiment description

An experiment consists of one or more runs.

Each run is an evolutionary optimization using a solver (an IterativeSolver of JGEA) on a problem with a random generator.

The description of an experiment also includes information on if/how/where to store the info about ongoing runs: zero or more listeners can be specified to listen to the ongoing evolutionary runs and save salient information. One reasonable choice is to use a ea.listener.bestCsv() (see below) to save one line of a CSV file for each iteration of each run. This way you can process the results of the experiment offline after it ended using, e.g., R or Python.

You can describe an experiment through an experiment file containing a textual description of the experiment. The description must contain a named parameter map for an experiment, i.e., its content has to be something like ea.experiment(...) (see the ea.experiment() builder documentation and the examples given below).

Named parameter map format

A named parameter map is a map (or dictionary, in other terms) with a name. It can be described with a string adhering the following human- and machine-readable format described by the following grammar:

<npm> ::= <n>(<nps>)
<nps> ::= ∅ | <np> | <nps>;<np>
<np> ::= <n>=<npm> | <n>=<d> | <n>=<s> | <n>=<lnpm> | <n>=<ld> | <n>=<ls>
<lnmp> ::= (<np>)*<lnpm> | <i>*[<npms>] | +[<npms>]+[<npms>] | [<npms>]
<ld> ::= [<d>:<d>:<d>] | [<ds>]
<ls> ::= [<ss>]
<npms> ::= ∅ | <npm> | <npms>;<npm>
<ds> ::= ∅ | <d> | <ds>;<d>
<ss> ::= ∅ | <s> | <ss>;<s>

where:

• <npm> is a named parameter map;
• <n> is a name, i.e., a string in the format [A-Za-z][.A-Za-z0-9_]*;
• <s> is a string in the format ([A-Za-z][A-Za-z0-9_]*)|("[^"]+");
• <d> is a number in the format -?[0-9]+(\.[0-9]+)? (or Infinity or -Infinity);
• <i> is a number in the format [0-9]+;
• ∅ is the empty string.

The format is reasonably robust to spaces and line-breaks.

An example of a syntactically valid named parameter map is:

car(dealer = Ferrari; price = 45000)

where dealer and price are parameter names and Ferrari and 45000 are parameter values. car is the name of the map.

Another, more complex example is:

office(
  head = person(name = "Mario Rossi"; age = 43);
  staff = [
    person(name = Alice; age = 33);
    person(name = Bob; age = 25);
    person(name = Charlie; age = 38)
  ];
  roomNumbers = [1:2:10]  
)

In this case, the head parameter of office is valued with another named parameter map: person(name = "Mario Rossi"; age = 43); staff is valued with an array of named parameter maps.

The * and + operators

Note the possible use of * for specifying arrays of named parameter maps (broadly speaking, collections of them) in a more compact way. For example, 2 * [dog(name = simba); dog(name = gass)] corresponds to [dog(name = simba); dog(name = gass); dog(name = simba); dog(name = gass)]. A more complex case is the one of left-product that takes a parameter $p$ valued with an array $v_1, \dots, v_k$ (on the left) and an array $m_1, \dots, m_n$ of named parameter maps (on the right) and results in the array of named parameter maps $m^\prime_{1,1}, \dots, m^\prime_{1,k}, \dots, m^\prime_{n,1}, \dots, m^\prime_{n,k}$ where each $m'_{i,j}$ is the map $m_i$ with a parameter $p$ valued $v_k$.

(size = [m; s; xxs]) * [hoodie(color = red)]

corresponds to:

[
  hoodie(color = red; size = m);
  hoodie(color = red; size = s);
  hoodie(color = red; size = xxs)
]

The + operator simply concatenates arrays. Note that the first array has to be prefixed with + too.

An example of combined use of * and + is:

+ (size = [m; s; xxs]) * [hoodie(color = red)] + [hoodie(color = blue; size = m)]

that corresponds to:

[
  hoodie(color = red; size = m);
  hoodie(color = red; size = s);
  hoodie(color = red; size = xxs);
  hoodie(color = blue; size = m)
]

Specification for the experiment file

You describe an experiment and its components using a named parameter map in a text file: in practice, each map describes a builder of a component along with its parameters. The complete specification for available maps, parameters, and corresponding values for a valid description of an experiment is available here.

In the following sections, we describe the key elements. For better organizing them, the builders are grouped in packages, whose names are something like sim.agent, ea.solver, and alike.

Embodied agents

There are five available embodied agents (i.e., robots). Their builders are grouped in the sim.agent package. Here we describe the most significant ones.

Voxel-based Soft Robots

sim.agent.centralizedNumGridVSR() corresponds to a Voxel-based Soft Robot (VSR) with a single closed-loop controller taking as input the sensor readings and giving as output the activation values, as described in [1]. The controller is a NumericalDynamicalSystem, i.e., a multivariate time-variant dynamical system taking the current time $t$ and $m$ real values (the sensor readings) and giving $n$ real values (the expansion/contraction values for each one of the $n$ voxels) while possibly updating its internal state. The sensors and the shape of the body are specified in the body parameter of sim.agent.centralizedNumGridVSR(). Available functions for the controller are grouped in the ds.num package: the key ones are described below. 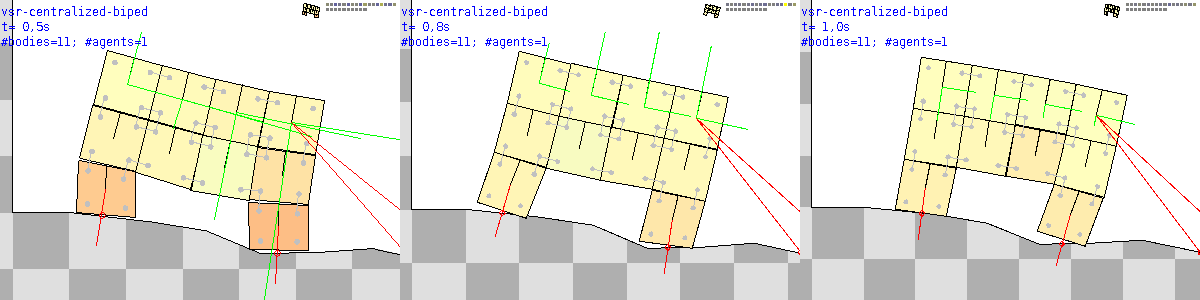Here is how an agent built with sim.agent.centralizedNumGridVSR() looks like with this description of a sim.agent.vsr.shape.biped() shape.

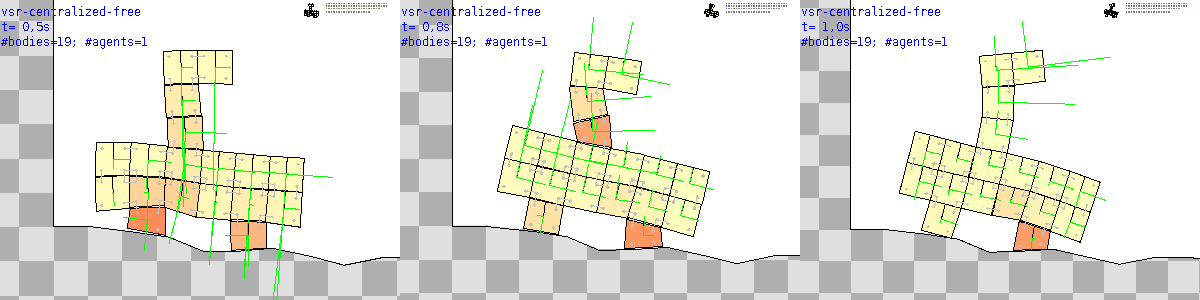
Here is instead a sim.agent.centralizedNumGridVSR() built with this description of a sim.agent.vsr.shape.free() shape, where 1 and 0 denote, in the s parameter, the presence or absence of a soft voxel in a 2D grid.

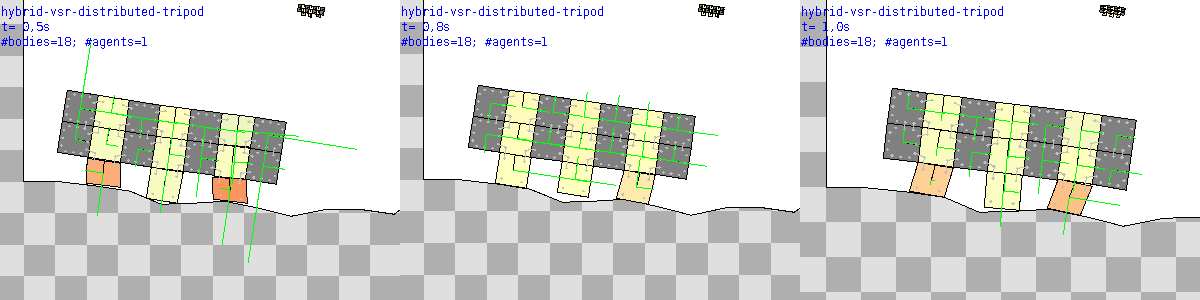
sim.agent.distributedNumGridVSR() corresponds to a VSR with a distributed controller, i.e., with one NumericalDynamicalSystem inside each one of the voxels. Each NumericalDynamicalSystem takes as input the local sensor readings and some (exactly signals for each one of the 4 adjacent voxels) values coming from adjacent voxels and gives as output the local activation value and some values going to adjacent voxels, as described in [1]. Depending on the mapper (see below), the same dynamical system is used in each voxel (with evorobots.mapper.numericalParametrizedHeteroBrains()) or different functions are used (with evorobots.mapper.numericalParametrizedHomoBrains()). That is, they for the former case, the dynamical systems share the parameters: in this case, each voxel in the body has to have the same number of sensors. 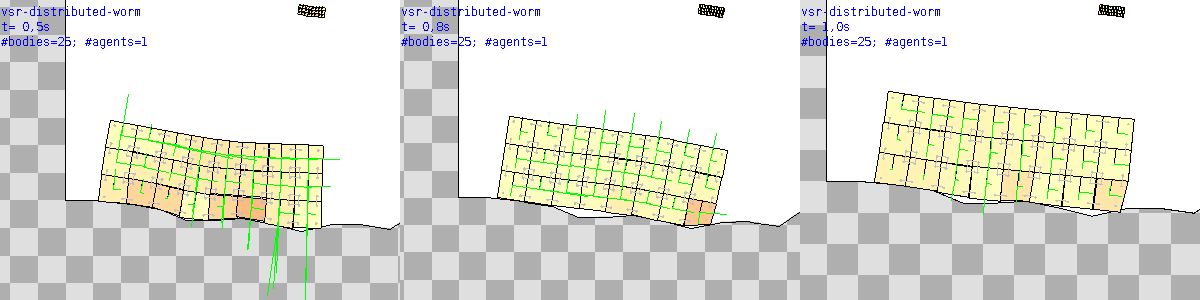Here is how an agent built with sim.agent.distributedNumGridVSR() looks like with this description of a sim.agent.vsr.shape.worm() shape.

Finally, note that voxels can either be soft or rigid: hybrid, i.e., including both types of voxels, VSRs can be created with sim.agent.vsr.shape.free(), using s for soft and r for rigid at each position. Here is how an agent built with sim.agent.distributedNumGridVSR() looks like with this description of a tripod-like shape including both rigid and soft voxels.

Numerical dynamical systems

Numerical dynamical systems take the current time $t$ and $m$ real values and give $n$ real values and possibly updates the internal state ("possibly" because some of them do not actually have a state, i.e., they are stateless, hence just multivariate functions $f: \mathbb{R}^m \to \mathbb{R}^n$). Here, numerical dynamical systems are used inside robots as controllers (or brains). Their builders are grouped in the ds.num.function package. Note that all the builders in this package actually return a builder of a NumericalDynamicalSystem (or something that extends it), rather than a NumericalDynamicalSystem: when using a builder as a controller of an agent, the builder is invoked with the appropriate values for $m$ and $n$ base, usually, on the body (shape and sensors) of the agent. Here we describe the most significant ones.

ds.num.mlp() is a Multi-layer Perceptron consisting of nOfInnerLayers inner layers in which each neuron has the same activationFunction. The size (number of neurons) inside each layer is computed based on the size of the first (input) and last (output) layers using the parameter innerLayerRatio: in brief, the $j+1$-th layer size is innerLayerRatio times the size of the $j$-th layer. As explained above, the size of the first and last layer are determined based on the context the function is used in (this holds for all the functions in this package). ds.num.mlp() is a NumericalParametrized dynamical system (actually a stateless dynamical system, that is, a function): its parameters are the weights of the MLP. Usually, they are exactly what you want to optimize using an evolutionary algorithm.

ds.num.sin() is a simple function that determines the output in $\mathbb{R}^n$ using an array of $n$ sinusoidal functions, i.e., $a \sin(2 \pi f t + \phi)+b$. Note that the input is not used when computing the output: that is, controllers employing (only) this function are open-loop controllers, since they do not use the sensor readings. The function is NumericalParametrized but the actual number of parameters depends on $n$ and the a, f, p, and b parameters, that are ranges. For each one, if the range boundaries do not coincide, the actual value of the corresponding sinusoidal parameter (i.e., $a$, $f$, $\phi$, $b$, respectively) is a parameter and is min-max normalized from $[-1,1]$ to the range. For example, take the following sin() for $n=10$:

ds.num.sin(
  a = s.range(min = 0.1; max = 0.3);
  f = s.range(min = 0.3; max = 0.3);
  p = s.range(min = -1.57; max = 1.57);
  b = s.range(min = 0; max = 0)
)

All the 10 sinusoidal functions will have the same frequency $f=0.3$ and the same bias $b=0$, but they will potentially differ in the amplitude $a \in [0.1, 0.3]$ and the phase $\phi \in [-1.57, 1.57]$. This function will have $10 \cdot 2 = 20$ parameters.

ds.num.enhanced() is a composite dynamical system that wraps another inner dynamical system. It takes an input of $n$ values and delivers to the inner dynamical system an enlarged input of (up to, depending on types parameter) $3n$ values, consisting of current (at $t$) values (i.e., exactly its $n$ input values), average values in the last windowT simulated seconds, and trend values (i.e., newest minus oldest) in the same time window.

ds.num.outStepped() is a composite dynamical system that wraps another inner dynamical system. It acts similarly to enhanced(), but operates on the output instead of on the input. It lets inner compute the output $\vec{x}$ of $m$ values passing it the untouched input and delivers as output $\vec{x}$ kept constant for consecutive time windows of stepT seconds. In other words, outStepped() makes inner a step dynamical system. It may be useful for avoiding high-frequency behaviors, like in [3], where stepT was set to 0.2. There is a similar composite dynamical system working on the input, ds.num.inStepped(), and one working on both input and output, ds.num.stepped().

ds.num.noised() is a composite dynamical system that wraps another inner dynamical system. It is a dynamical system that adds some Gaussian noise before (with inputSigma $> 0$) and/or after (with outputSigma $> 0$) invoking the inner function.

Problems

There is currently a single kind of problem available, the ea.problem.totalOrder(). It represents an optimization problem in which the objective can be sorted with a total order: usually, it is a number. This kind of problem is defined by a function qFunction for assessing the solution (usually an agent) and producing a quality Q, a function cFunction for transforming a Q in a C implements Comparable<C>, and a type value specifying if the goal is to minimize or maximize the Cs. In practice, the qFunction is a task runner (sim.taskRunner()) and the cFunction specifies how to extract a number out of the task outcome, like in this example (taken from this example experiment):

ea.p.totalOrder(
  qFunction = s.taskRunner(task = s.task.locomotion());
  cFunction = s.task.locomotion.xVelocity();
  type = maximize
)

Tasks

There are a few available tasks. Their builders are grouped in the sim.task package.

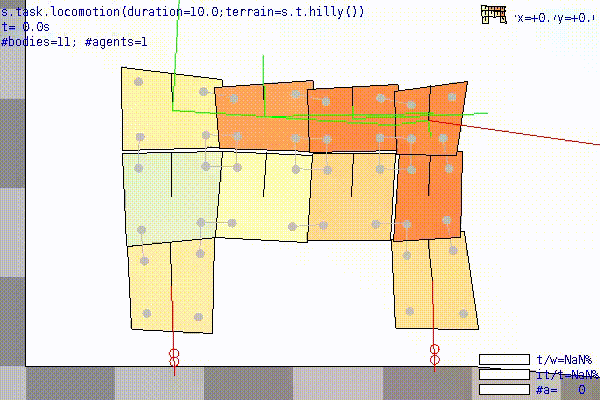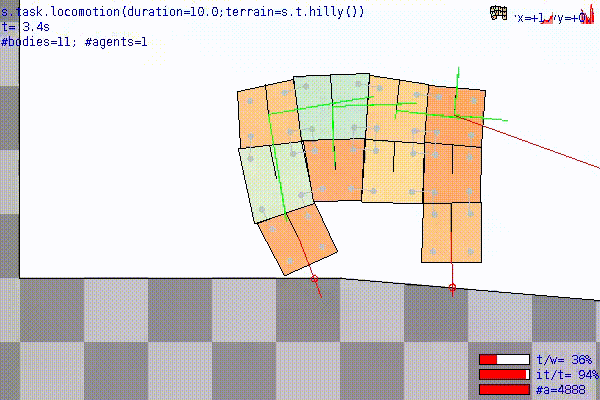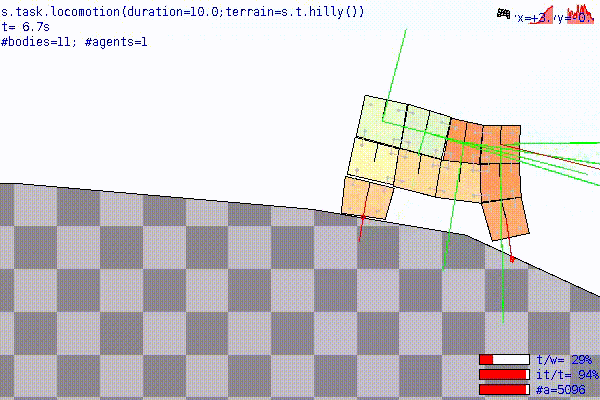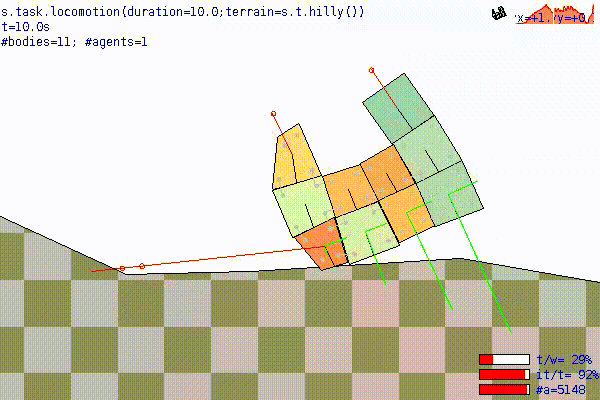
The most significant is sim.task.locomotion(). Here, the robot is put on a terrain (see here for the options) and let move for duration simulated seconds. The usual goal in terms of optimization is to maximize the velocity of the robot, that can be extracted from the task outcome with sim.task.locomotion.xVelocity().

Solvers

Solvers correspond to evolutionary algorithms. In principle, any solver implemented in JGEA might be used; currently, however, only a few are available here. Their builders are grouped in the ea.solver package. In general, a solver is a way for iteratively search a solution in $S$ (the solution oor phenotype space) whose quality is defined in $Q$ (the quality or fitness space): in most cases, the actual search occurs in a third space $G$, the genotype space, where it's easier to define some genetic operators. See [2] for a more detailed description of the abstractions of search, solution, and fitness spaces. When evolving simulated robotic agents, as in the case of 2d-robot-evolution, an $s \in S$ is a robotic agent (actually a Supplier<Agent>), and a genotype $g \in G$ is a more tractable entity, like a vector $\vec{g} \in \mathbb{R}^p$ (in Java terms, a List<Double>). For mapping a $g$ into a $s$, the solver uses a genotype-to-phenotype mapper, that is a parameter of the solver (mapper).

Two common solvers are GA and ES: both are able to work with real numbers, i.e., with $G = \mathbb{R}^p$. Note that you are not required to say what's the value of $p$: it is inferred automatically from the mapper, which is indeed a InvertibleMapper<List<Double>, S> that in turn infers the size of a genotype from a target phenotype.

ea.solver.doubleStringGa() is a standard GA working on $\mathbb{R}^p$. It iteratively evolves nPop individuals until nEval fitness evaluations have been done. Individual genotypes are initially generated randomly with each element in [initialMinV, initialMaxV]; then, they are modified by applying a Gaussian mutation with sigmaMut after a uniform crossover. Selection is done through a tournament with size tournamentRate $\times$ nPop (clipped to the lowest value of minNTournament).

ea.solver.simpleEs() is a simple version of Evolutionary Strategy (ES). After the same initialization of ea.solver.simpleEs(), it evolves by taking, at each iteration, the best parentsRate rate of the population, computing their mean value, and producing the next generation by sampling a multivariate Gaussian distribution with the computed mean and sigma. At each iteration, the nOfElites individuals are copied to the next generation.

Mappers

The mapper maps a genotype to a robot, using the target of the run "as the starting point". Available mappers are in the evorobots.mapper package.

The two most significant mapper are based on the NumBrained and NumMultiBrained interfaces that model, respectively, agents that have one or many brains, respectively (the former being a particular case of the latter). Both the evorobots.mapper.numericalParametrizedHomoBrains() and evorobots.mapper.numericalParametrizedHeteroBrains() assume that the brain or brains are Parametrized, i.e., they work based on a vector of numerical parameters $\vec{\theta} \in \mathbb{R}^p$: hence mapping a List<Double> to the robot simply amounts to injecting the parameters in the brains. For evorobots.mapper.numericalParametrizedHomoBrains(), the same $\vec{\theta}$ is injected in every brain; for evorobots.mapper.numericalParametrizedHeteroBrains() one chunk of a larger vector is injected as $\vec{\theta}$ for every brain.

All the numerical dynamical systems listed above are Parametrized: the composite ones delegate to the inner function.

Listeners

Listeners are notified at each iteration during the evolution and at the end of each run. They can be used to save, typically on a file, useful information concerning the evolution. Their builders are grouped in the ea.listener package. Here we describe the most significant ones.

ea.listener.bestCsv() writes a single CSV file for the experiment. If the file at filePath already exists, a new file with a similar name is used, without overwriting the existing file. The CSV will have one row for each iteration of each run and one column for each of the elements of defaultFunctions, functions, and runKeys. Values for functions are of type NamedFunction (i.e., functions with a name) whose builders are in the ea.namedFunction package: usually, compose a few of them for obtaining a function that takes a state POSetPopulationState<G, S, Q> of the evolution and returns the information of interest. For example, for having a column with the size of the best genotype (i.e., $p$ when $\vec{g} \in \mathbb{R}$, i.e., with all the solvers above), you set:

functions = [
  ea.nf.size(f = ea.nf.genotype(individual = ea.nf.best()); s = "%5d")
]

runKeys are pairs of strings specifying elements of the run description to be extracted as cell values (as name and value). Each value string specifies both which part of the run description to extract and, optionally, the format, using the format specifier of Java printf() method (for run elements being named maps, the special format %#s just renders the name of the map). The format of the value has to be {NAME[:FORMAT]}, e.g., {randomGenerator.seed}, or {problem.qFunction.task.terrain:%#s}. For instance, ea.misc.sEntry(key = "solver"; value = "{solver:%#s}") specifies a pair of a name solver and a value that will be the solver key of the run, only by name (e.g., ea.solver.doubleStringGa).

ea.listener.telegram() sends updates about the current run via Telegram. In particular, at the end of each run it can send some plots (see the ea.plot package) and zero or more videos (see evorobots.video()) of the best individual found upon the evolution performing the tasks described in tasks, not necessarily including the one used to drive the evolution. This listener requires a chatId and a Telegram botId that has to be the only content of a text file located at botIdFilePath. The example below shows how to make this listener to send a plot of the fitness of the best individual during the evolution and a video of it performing locomotion on a flat terrain (XXX has to be replaced with an actual number).

ea.l.telegram(
  chatId = "XXX";
  botIdFilePath = "../tlg.txt";
  plots = [
    ea.plot.fitness(f = ea.nf.f(outerF = s.task.l.xVelocity()); sort = max; minY = 0)
  ];
  accumulators = [
    er.video(
      task = s.task.locomotion(terrain = sim.terrain.flat(); duration = 60; initialYGap = 0.1);
      endTime = 60
    )
  ]
);

ea.listener.tui() shows a text-based user interface summarizing the progress of the experiments. See the example below for the usage of this listener.

evorobots.listener.videoSaver() can be used to save a video of one individual (in the default case, the best of the last generation).

Examples of experiment files

Example 1: 3 runs with a VSR biped

a.experiment(
  runs = (randomGenerator = (seed = [1:1:3]) * [ea.rg.defaultRG()]) * [
    ea.run(
      solver = ea.s.doubleStringGa(
        mapper = er.m.numericalParametrizedHeteroBrains(target = s.a.centralizedNumGridVSR(
          body = s.a.vsr.gridBody(
            sensorizingFunction = s.a.vsr.sf.directional(
              headSensors = [s.s.sin(f = 0); s.s.d(a = -15; r = 5)];
              nSensors = [s.s.ar(); s.s.rv(a = 0); s.s.rv(a = 90)];
              sSensors = [s.s.d(a = -90)]
            );
            shape = s.a.vsr.s.biped(w = 4; h = 3)
          );
          function = ds.num.mlp()
        ));
        nEval = 1000;
        nPop = 25
      );
      problem = ea.p.totalOrder(
        qFunction = s.taskRunner(task = s.task.locomotion(duration = 15));
        cFunction = s.task.locomotion.xVelocity();
        type = maximize
      )
    )
  ];
  listeners = [
    ea.l.tui(
      functions = [
        ea.nf.size(f = ea.nf.genotype(individual = ea.nf.best()); s = "%5d");
        ea.nf.bestFitness(f = ea.nf.f(outerF = s.task.l.xVelocity(); s = "%5.2f"));
        ea.nf.fitnessHist(f = ea.nf.f(outerF = s.task.l.xVelocity()))
      ];
      runKeys = [
        ea.misc.sEntry(key = "seed"; value = "{randomGenerator.seed}")
      ]
    );
    ea.l.expPlotSaver(
      filePath = "plot-fitness.png";
      freeScales = true;
      plot = ea.plot.fitnessPlotMatrix(
        yFunction = ea.nf.bestFitness(f = ea.nf.f(outerF = s.task.l.xVelocity(); s = "%5.2f"))
      )
    );
    ea.l.bestCsv(
      filePath = "best-biped-mlp.txt";
      functions = [
        ea.nf.size(f = ea.nf.genotype(individual = ea.nf.best()); s = "%5d");
        ea.nf.bestFitness(f = ea.nf.f(outerF = s.task.l.xVelocity(); s = "%5.2f"))
      ];
      runKeys = [
        ea.misc.sEntry(key = "seed"; value = "{randomGenerator.seed}")
      ]
    );
    er.l.videoSaver(videos = [
      er.video(task = s.task.locomotion(duration = 15; terrain = s.t.hilly()); w = 300; h = 200)
    ])
  ]
)

This experiment consists of 3 runs differing only in the randomSeed (seed = [1:1:3]). Instead of specifying three times the full content of a run(...) (that would have been different in just the random seed), here the * operator is used.

The target robot is a $4 \times 3$ biped with a centralized brain consisting of an MLP; the brain exploits the sensors installed in the body: here distance (s.s.d()), area ratio (s.s.ar()), rotated velocity (s.s.rv()). The available sensor builders are grouped in the sim.sensor package (they correspond to methods of the utility class Sensors of 2dmrsim.) The solver is a simple GA with a population of 25 individuals. The task is the one of locomotion on a flat terrain, lasting 15 simulated seconds.

The experiment produces a CSV file located at best-biped-mlp.txt. The file will include also a column named seed with the random seed of the run and a column solver with the solver (with a constant value, here).

The experiment also saves, after each run, a video of the best individual which runs on a different terrain than the one it was evolved on (s.t.hilly() instead of s.t.flat()). The saved video might look like this:

Note that this is the result of a rather short (nEval = 1000) evolution; moreover, the best robot is here facing a terrain "it never saw" (more precisely, it and its entire ancestry never saw it) during the evolution.

Example 2: 10 runs with 3 VSR bodies on 2 terrains

ea.experiment(
  runs = (randomGenerator = (seed = [1:1:10]) * [ea.rg.defaultRG()]) *
  (problem = (qFunction = [
    s.taskRunner(task = s.task.locomotion(terrain = s.t.flat(); duration = 20));
    s.taskRunner(task = s.task.locomotion(terrain = s.t.hilly(); duration = 20))
  ]) * [
    ea.p.totalOrder(
      cFunction = s.task.locomotion.xVelocity();
      type = maximize
    )
  ]) * (solver = (mapper = (target = (body = (shape = [
    s.a.vsr.s.worm(w = 8; h = 3);
    s.a.vsr.s.free(s = "111110-110011");
    s.a.vsr.s.worm(w = 5; h = 2)
  ]) * [
    s.a.vsr.gridBody(      
      sensorizingFunction = s.a.vsr.sf.uniform(
        sensors = [s.s.ar(); s.s.rv(a = 0); s.s.rv(a = 90); s.s.a()]
      )
    )
  ]) * [
    s.a.distributedNumGridVSR(
      signals = 2;
      function = ds.num.mlp()
    )]
  ) * [er.m.numericalParametrizedHomoBrains()]
  ) * [ea.s.doubleStringGa(nEval = 1000; nPop = 50)]
  ) * [ea.run()];
  listeners = [
    ea.l.tui(
      functions = [
        ea.nf.bestFitness(f = ea.nf.f(outerF = s.task.l.xVelocity(); s = "%5.2f"));
        ea.nf.fitnessHist(f = ea.nf.f(outerF = s.task.l.xVelocity()))
      ]
    )
  ]
)

Here there is just one listener, just for simplifying the example; in practice it would be weird to run such a big experiment without saving any data.

A single solver is used to solve two tasks:

• s.taskRunner(task = s.task.locomotion(terrain = s.t.flat(); duration = 20))
• s.taskRunner(task = s.task.locomotion(terrain = s.t.hilly(); duration = 20));

with three robot shapes:

• s.a.vsr.s.biped(w = 4; h = 3)
• s.a.vsr.s.free(s = "111110-110011")
• s.a.vsr.s.worm(w = 5; h = 2)

each time with 10 different random seeds. There will hence be 60 runs.

Player

You can execute a single task on a single agent, instead of performing an entire experiment consisting of several runs, using Player. It can be started with

java -cp 2d-robot-evolution/io.github.ericmedvet.robotevo2d.main/target/robotevo2d.main-1.5.0-jar.with-dependencies.jar io.github.ericmedvet.robotevo2d.main.Player --playFile <play-file>

where <play-file> is the path to a file with an play description (see evorobots.play()).

For example, with a play file like this:

er.play(
  mapper = er.m.numericalParametrizedHeteroBrains(target = s.a.centralizedNumGridVSR(
    body = s.a.vsr.gridBody(
      sensorizingFunction = s.a.vsr.sf.directional(
        headSensors = [s.s.sin(f = 0);s.s.d(a = -15; r = 5)];
        nSensors = [s.s.ar(); s.s.rv(a = 0); s.s.rv(a = 90)];
        sSensors = [s.s.d(a = -90)]
      );
      shape = s.a.vsr.s.biped(w = 4; h = 3)
    );
    function = ds.num.noised(outputSigma = 0.01; inner = ds.num.sin(
      a = s.range(min = 0.5; max = 0.5);
      f = s.range(min = 0.5; max = 0.5);
      p = s.range(min = -1.57; max = 1.57);
      b = s.range(min = 0; max = 0)
    ))
  ));
  task = s.task.locomotion();
  genotype = er.doublesRandomizer();
  consumers = [
    er.c.video(filePath = "results/video-after.mp4"; startTime = 5; endTime = 15; w = 300; h = 200)
  ];
  videoFilePath = "results/video-after.mp4"
)

you run a locomotion task on a biped VSR with a centralized brain consinsting of a sin() function with randomized phases. The result is saved as a video at results/video-after.mp4. If you don't want to save a video, use er.c.rtGUI() as an element of consumers.

References

1. Medvet, Bartoli, De Lorenzo, Fidel; Evolution of Distributed Neural Controllers for Voxel-based Soft Robots; ACM Genetic and Evolutionary Computation Conference (GECCO); 2020
2. Medvet, Nadizar, Manzoni; JGEA: a Modular Java Framework for Experimenting with Evolutionary Computation; Workshop Evolutionary Computation Software Systems (EvoSoft@GECCO); 2022
3. Medvet, Rusin; Impact of Morphology Variations on Evolved Neural Controllers for Modular Robots; XVI International Workshop on Artificial Life and Evolutionary Computation (WIVACE); 2022