APL Idioms & Solutions

Solutions of various problems in Dyalog APL

Note: An overview of the most used APL symbols can be found in this cheatsheet.

TODO

• Try running Dyalog APL in Jupyter Notebooks.
• Go through this cheatsheet for translating between Numpy (Python) and APL
• This Python code calculates Precision, Recall, Sensitivity, etc. Understand thoroughly (develop intuition) and translate to APL.

APL Competitions

• APL Forge - a competition where you can showcase APL projects/libraries

Resources

You can try most of the code below online at Try APL or ngn-apl.

NOTE: ngn-apl can also be used offline in a computer / phone after installing as a PWA (Progressive Web App).

Web Books

• Mastering Dyalog APL
• Learn APL
• APL Cultivations is another good book (by the same author)

Lists of Resources

• APL Cart - search here for various common APL idioms
• APL Wiki: Learning Resources list
• APL Wiki: Chat Rooms list (Reddit, Matrix, Facebook, etc.)
• Discord: APL Resources
• Discord: APL Recommendations
• APL News
• YouTube channel focusing on J language (a derivative of APL): https://www.youtube.com/@tangentstorm

Also Adám on The APL Farm (Discord) said this, haven't tried it:

If you're on Windows, then ⎕load'arachnid for an (old-style APL) implementation of a Windos GUI Spider Solitaire.

Neural Networks

• YouTube Series: Learn APL with Neural Networks
• Research Paper: Conventional Neural Networks with APL - see its complete code in its Github repo

Real World Applications built in APL

• Games (Web Apps) built in APL using MiServer framework
• Building web services with APL
• Pixel Art Editor in APL
• Subway Route Planner in APL

TODO

• Study the Power Operator ⍣ operator as a (possible) replacement for while loop.

Workspaces

• ⎕CY 'dfns' is equivalent to from dfns import * in Python - i.e., import everything unqualified from given workspace.
• Dfns Workspace is built-in, has many useful functions.

⎕CY 'dfns'   ⍝ Import built-in workspace 'dfns'
2 pco 30     ⍝ Prime Factorization of 30, using 'pco' function from 'dfns'

Benchmarking / Profiling

• ]PERFORMANCE.runtime '10?10' - measure execution time of the code (which is written in a string)
• ⎕AI - gives compute time since start of APL session (along with other information)
• ∘.(=×⊢)⍨⍳N is ~200x slower than A ← N N⍴0 ⋄ A[,⍨¨⍳N] ← ⍳N for creating a Diagonal Matrix for N←1000 - I measured this with ]PERFORMANCE.runtime!

Basic Idioms

• ≠ (Monadic: Unique Mask, Dyadic: Not Equals)

≠1 2 1 2 4 4 5 2 1   ⍝ 1 2 0 0 1 0 1 0 0 - Unique Mask: mark first occurance of value in list as 1, rest as 0
3 1≠4 1      ⍝ 1 0 - Not Equals

• ! (Monadic: Factorial, Dyadic: nCr):

!5      ⍝ 120 - Factorial of 5
3!5     ⍝ nCr (n=5, r=3) <- No. of combinations of r units from total n units

• ⍷ (Dyadic only) - Finds starting positions of substring in string. Example:

'issi' ⍷ 'Missisipi'   ⍝ 0 1 0 0 1 0 0 0 0 0

• ↑ (Dyadic: Take first N elems, Monadic: Mix / converts a vector of vectors to a single matrix of scalars)

⍝ If we try to take more elements than size of argument, then rest are padded with 0s
5↑1 4        ⍝ 1 4 0 0 0
¯3↑'missisipi'  ⍝ negative index means take from end - 'ipi'

• ⍕ (Dyadic: Format / Round) right argument to N decimal places, where N is left argument. If N=0, then this is same as finding nearest integer to number.
• @ At operator - replace elements in an array at indices by some values. Has variants - eg. you can pass a function to determine which indices to replace at, and a function to determine the replacement value at positions.

User Defined Functions

• Create a dfn style function that takes inputs: right argument ⍵, and optionally left argument ⍺.
• An ambivalent function can be called monadically (with one argument) or dyadically (with 2 arguments). One way to define ambivalent function is a dfn with default left argument:

f ← {⍺←0 ⋄ ⍺ ⍵}    ⍝ ⍺ has default value 0
f 2                ⍝ monadic (one argument) use             
1 f 2              ⍝ dyadic (2 arguments) use

Matrix

• Laminate (comma with fractional axis) can:
  • Join vectors into matrix as rows - A,[0.5]B
  • Join vectors into matrix as columns - A,[1.5]B
  • Also works for higher dimensions (see link).

String Functions

• ⊢⊂⍨1,' '∘= - function to split string into words
• +/∘.= - Letter frequencies of some characters (left argument) in a string (right argument) (similar to Python's collections.Counter class):

Complex Numbers

a ← 1j2    ⍝ Complex No. (Real = 1, Imaginary = 2)
9○a        ⍝ Get Real Part
11○a       ⍝ Get Imaginary Part

⍝ Monadic × gives sign of real numbers, but does something different with complex numbers: 
×3J4       ⍝ 0.6J0.8 - complex number with same phase but magnitude 1

This is the Circle Operator, which can be used to perform these and other trignometric operations.

Note:

• Passing a negative number as left argument gives inverse of ordinary function (eg. sine becomes inverse sine).
• Example: 11○a gives imaginary component of a, so ¯11○a "puts back" real a into imaginary component. In other words, ¯11○a is the same as multiplying a with iota 0J1.

Date & Time

See the reference.

 ⎕CY'dfns'                ⍝ load workspace dfns (built-in)
 ⎕TS timestamp 'Now'      ⍝ get current timestamp, and format it

Time of Day

Text  ← 'night' 'evening' 'afternoon' 'morning'
Hours ← 19 18 12    ⍝ starting hours corresponding to the times of day in above variable Text
                    ⍝ starting hour (0) of morning is omitted because it is not required
timeOfDay ← ⊃Text⌷⍨(1⍳⍨Hours≤⊢)   ⍝ function that takes hour (0-23) as input, returns string (time of day)

Algebra

• Primary Diagonal of a Matrix - 1 1∘⍉

• Sum of Vector Magnitudes - .5+.*⍨2+.*⍨⊢ where (single) argument is a 2D Matrix whose each row is one vector.

• Solve System of Linear Equations - (⌹⊢)+.×⊣ (uses Matrix Inverse Operator ⌹)

  • right argument is coefficient matrix
  • left argument is vector of equation constants

• Function to evaluate a polynomial at a value - ⊤⍣¯1 where:

  • right argument is an array of coefficients of polynomial (highest power to lowest (constant) power)
  • left argument is value at which polynomial is to be evaluated.

• Function to compare two arrays by priority - ×1↑0,⍨(0~⍨-), i.e., first compare first elements, then second elements, and so on until the arrays diverge. The result is 1 (Left > Right), ¯1 (Left < Right) or 0 (Left = Right).

• {∘.(=×⍵⌷⍨⊢)⍨⍳≢⍵} - function to create diagonal matrix using array

• $sin(x)$ using Taylor expansion $x - x^3/3! + x^5/5! - x^7/7! ...$

⎕IO ← 0
sin ← {⍺←100 ⋄ (⍺⍴1 ¯1)+.×(!÷⍨⍵∘*)1+2×⍳⍺}
sin 0          ⍝ example - sin(0)
100 sin ○.5    ⍝ example - sin(pi/2) using 100 values of Taylor expansion

Note: This works in ngn-apl but raises DOMAIN ERROR in Dyalog APL.

Computer Network

• Hemming Distance - +.(|-)
  • Number of bits where two binary sequences differ.

Statistics - APL Functions

Note: Unless otherwise noted, the inputs to all listed functions are 1-D Arrays.

Monadic (Single Argument) Functions

• Frequency Count - {⍺ (≢⍵)}⌸ (returns 2D matrix whose first column is unique elements, and second column is their frequencies)
  • See explanation for Key Operator ⌸ here.
• Arithmetic Mean / Average - avg ← +/÷≢
• Running Average - +\÷(⍳≢)
• Geometric Mean - gmean ← ×/*(÷≢)
• Harmonic Mean - hmean ← {÷+/÷⍵}×≢
• Variance - var ← (2+.*⍨⊢-avg)÷¯1+≢
• Standard Deviation / RMS (Root Mean Square) - stddev ← .5*⍨var

Dyadic (Two Argument) Functions

Note: Each function below has left argument Frequencies, right argument Data. Both arguments are 1-D arrays.

• Inner Product / Weighted Mean / Arithmetic Mean for Sample Proportions - ip ← +.×
• Variance for Sample Proportions - varsample ← +.× ∘ ((2*⍨⊢-avg)⊢)
• Sigmoid Function - sigmoid ← {÷1+*-⍵÷⍺}
  • Right Argument ⍵ is actual input
  • Left Argument ⍺ is called Temperature (just a mathematical term!)
• Pearson Correlation Coefficient - `correlation ← (+.×÷0.5*⍨×⍥(+/*∘2))⍥(⊢-+/÷≢)

Operators (Higher Order Functions) - take functions as argument

• Stochastic / Probability Function - {(?0⍴⍨⍵)≥⍺⍺⍳⍵} - output 1 or 0 with probability given by Probability Function ⍺⍺ (input)
  • Example - 10∘sigmoid{(?0⍴⍨⍵)≥⍺⍺⍳⍵}10

Plotting / Graphing

• ]plot - plots a vector on Y Axis, index on X Axis. Plot is continous by default.
• Example - Plot sigmoid function with 100 data points - ]plot sigmoid ⍳100

Stochastic / Probabilistic Plots

• Random Walk

N ← 1000                               ⍝ no. of data points. Plot becomes more detailed with increased N
random_walk ← {⍵+|+\⍺,0.5-?N⍴0}        ⍝ ⍵ ← minimum stock value (≥ 0), ⍺ ← initial investment
]plot 47 random_walk 0.5

Note: N (global variable) controls the no. of data points in the plot. Plot becomes more detailed with increased N.

• Random Walk with Upward Drift

N ← 10000                          ⍝ Very detailed plot
D ← 0.01                           ⍝ drift per day
]plot (D*⍳N) + 0 random_walk 0.5

File I/O

• Parsing Files - Text, CSV, XML, HTTP
• Change Working Directory - ]CD 'directory-path-here'
• JSON (detailed)

Misc

Functions

• Softmax: Output activation function for multi-class classifier Neural Networks: (⊢÷+/)*
• Calcuating tax according to tax slabs:

tax_calculate ← {(⍺[;2]÷100)+.×2-/⍵,⍺[;1]}      

⍝ This line means: >Rs. 10L => 35% Tax, >Rs. 7L => 20% Tax, >Rs. 5L => 35% Tax, >Rs. 0L => 0% Tax
M ← ↑(10 35) (7 20) (5 15) (0 0)           ⍝ Left column of matrix is in Rs. Lakhs, second column is Tax %
X ← 100                                    ⍝ Rs. Lakhs
M tax_calculate X                          ⍝ Returns: 32.4 (Rs. Lakhs)

• Number of times sorting directions (ascending or descending) change in a 1D array: ≢0~⍨2-/⊢
• Format complex number as its real and imaginary parts seperated by a space - ⊃9 11(⊣,' ',⊢)⍥⍕.○⊢
  • Example: 1j¯2 becomes the string '1 ¯2'.
• Add random noise to an array - ⊢+∘?0⍴⍨≢ (Note: Here, random noise means a random number between 0 and 1 is added to each element of array.)
• FizzBuzz function (array upto given argument) - {⊃(1+2⊥0=5 3|⍵)⌷⍵ 'Fizz' 'Buzz' 'FizzBuzz'}¨⍳
• Swastika Symbol - ' -|'[1+3∘.((0 2∊⍨-⍨)×(1+2|⊣))⍥⍳5] ⍝ 3 5⍴'| | - - | |'
• {((⊢<¯1∘↑)+\⍵)/⍵} - function that takes a boolean array and strips the last 1 (followed by all 0s)
• ↑(⊢,2∘*)⊂-⍳10 - table of negative powers of 2
• N←50 ⋄ A←N N⍴' ' ⋄ A[(⌈N×9 11,.○⊢)¨*0j1×○(⍳N-1)÷2×N] ← '*' ⋄ A - Prints an approximate quarter circle in a 50x50 grid.
• A,[0.5]'-' - Underlines string A using Laminate.
• Function that shows number spiral:

    spiral  ← {A ← ⍵ ⍵⍴' ' ⋄ B ← ¯1↓(9 11,.○⊢)¨+\(1j1×1+⌊⍵÷2),(⊃(⍴∘1¨2/⍳),.×1 0J1 ¯1 0J¯1⍴⍨2∘×)⍵-1 ⋄ A[B] ← 2 0∘⍕¨⍳≢B ⋄ A}
    spiral 5
 20  19  18  17 
  7   6   5  16 
  8   1   4  15 
  9   2   3  14 
 10  11  12  13 

• Function that puts boundary around matrix (right argument) using character (left argument):

       bounded ← {A←(2+s←⍴⍵)⍴⍺ ⋄ A[1+⍳s]←⍵ ⋄ A}
      '#' bounded ?4 3⍴10
#  # #  # #
# 10 5  9 #
#  4 2 10 #
#  3 8  9 #a
#  3 3  6 #
#  # #  # #

Real Life Problems

• Suppose we collect data on N characterstics of a large group of people. What is the probability that a person exists who falls within 1 Standard Deviation from Average for all characterstics?

To find out, let's tabulate probabilities using N from 1 to 20:

       (⊢,[1.5](0.68∘*))⍳20       
 1 0.68           
 2 0.4624         
 3 0.314432       
 4 0.21381376     
 5 0.1453933568   
 6 0.09886748262  
 7 0.06722988818  
 8 0.04571632397  
 9 0.0310871003   
10 0.0211392282   
11 0.01437467518  
12 0.00977477912  
13 0.006646849802 
14 0.004519857865 
15 0.003073503348 
16 0.002089982277 
17 0.001421187948 
18 0.0009664078048
19 0.0006571573073
20 0.000446866969 

Or plot the probabilities as a graph: ]plot 0.68*⍳20

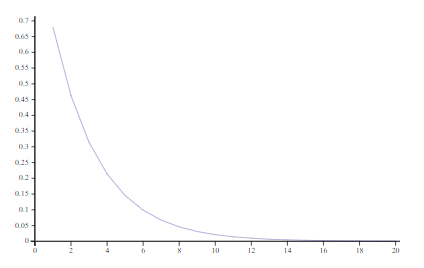
It's clear from both the table and the graph that the probability of the average person (who falls within 1 Standard Deviation in all charactestics) existing becomes very low as the no. of characterstics N increases.

In other words, the average person doesn't exist!

Untested

• (⎕NEW 'Bitmap' (⊂'File' 'image-filename')).CBits - Read an image's bitmap. Doesn't work on Linux. Supposed to work on Windows, but haven't tested it yet.