Gomoku

基本介绍

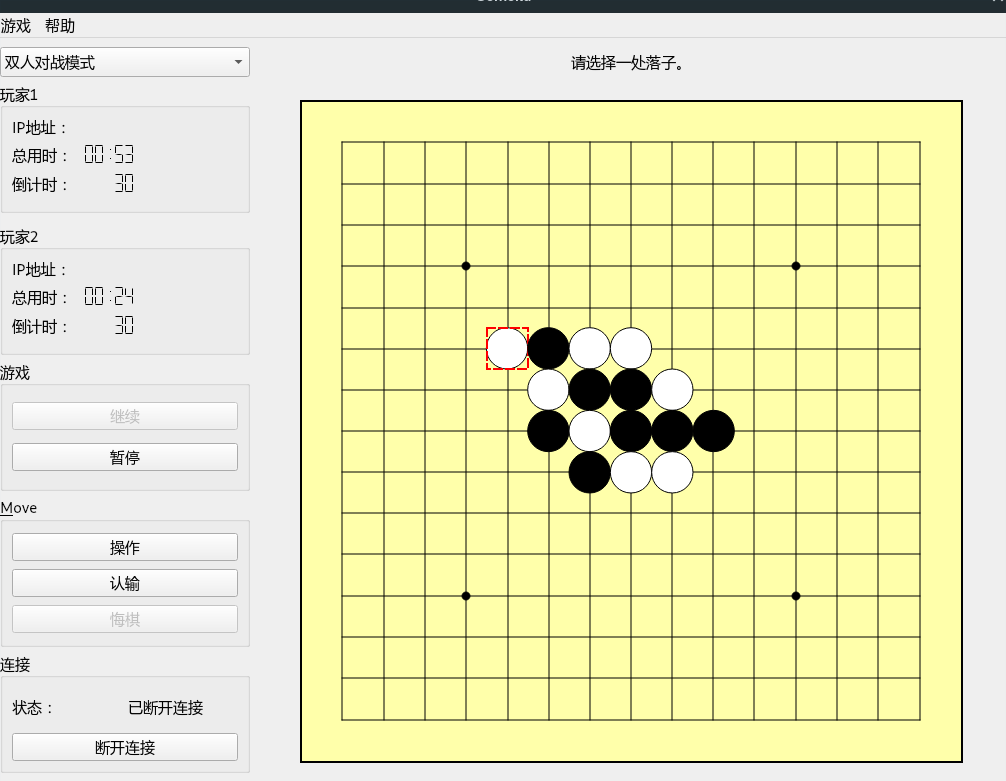
五子棋游戏(Gomoku), GUI通过Qt实现，如图所示：

游戏支持以下模式：

• Single Mode 双人对战模式，支持在同一台电脑上两人对战。
• Network Mode 网络对战模式，支持用户通过网络连接对战，只需要知道IP即可。
• AI Mode 人机对战模式，支持AI对战。

棋型确定

棋型	定义	图例
长连	至少五颗同色棋子连在一起
活四	有两个连五点（即有两个点可以形成五），图中白点即为连五点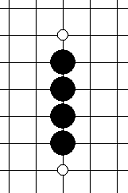
冲四	有一个连五点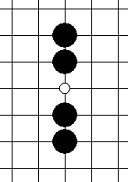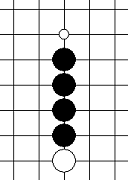
活三	可以形成活四的三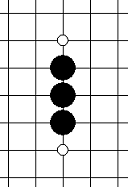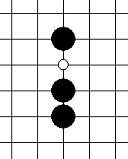
眠三	只能够形成冲四的三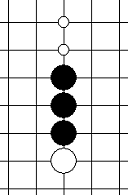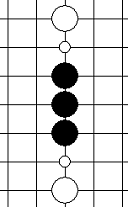
活二	能够形成活三的二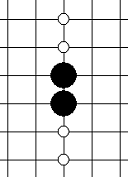
眠二	能够形成眠三的二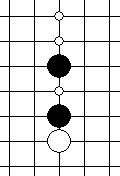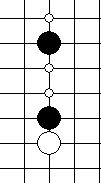
死四	两头都被封堵的四
死四	两头都被封堵的三

落子估值方式

分析：棋子落在哪里最好？

1. 需要考虑落下后会在四个方向各形成什么棋型，是否形成组合棋型，然后进行初步打分；
2. 同时还要考虑落子位置，一般同分情况下越中心的点越好；
3. 可以分析对攻击效果、防守效果、综合效果。

初步打分：

就是按照威胁程度给每种棋型打分，在理解棋型后，试验了多组估分方式，最后确定效果最好的一组打分方式如下：

棋型（含组合棋型）	分值
长连	100000
活4、双冲4、冲4活3	10000
双活3	5000
活3眠3	1000
眠4	500
活3	200
双活2	100
眠3	50
活2眠2	10
活2	5
眠2	3
死4	-5
死3	-5
死2	-5

再统计在四个方向各形成什么棋型，是否形成组合棋型，取最高分为初步打分的结果。

落子位置

根据棋盘分布问题，越中心的点分值应当越高。

static int[][] position = {
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0 },
{ 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0 },
{ 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 4, 4, 4, 4, 4, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 5, 6, 6, 6, 5, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 5, 6, 7, 6, 5, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 5, 6, 6, 6, 5, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 4, 4, 4, 4, 4, 4, 4, 3, 2, 1, 0 },
{ 0, 1, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 2, 1, 0 },
{ 0, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 0 },
{ 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };

棋局估值函数

函数描述：

有了落子估值方式后，可以针对某一棋局，分析一定棋盘范围内的各个可落子点的落子估值，将最大综合分作为该棋局的估值。

简单智能:

利用估值函数，即可实现简单智能，即只考虑当前局面下的最佳落子点，并落子。

优点是速度快，眼前胜利绝不放过，缺点也是显而易见的，对于埋伏了多步的杀法，这种只顾“近忧”的智能无能为力。因此，就需要搜索算法增加“远虑”。

搜索算法

计算机要选择有利于它的最佳下法，就要能够判断那种形式对自己最有利。为了判断哪种形式更有利，往往需要向后面计算几步，看看走了几步棋之后，局面的形式如何。五子棋的各种走法展开后，就形成了一棵巨大的博弈树。

极大极小搜索

在这个树中，从根节点为0开始，奇数层表示电脑可能的走法，偶数层表示玩家可能的走法。

假设电脑先手，那么第一层就是电脑的所有可能的走法，第二层就是玩家的所有可能走法，以此类推。

那么我们如何才能知道哪一个分支的走法是最优的，我们就需要一个估值函数能对当前整个局势作出评估，返回一个分数。我们规定对电脑越有利，分数越大，对玩家越有利，分数越小，分数的起点是0。

我们遍历这颗博弈树的时候就很明显知道该如何选择分支了：

• 电脑走棋的层我们称为MAX层，这一层电脑要保证自己利益最大化，那么就需要选分最高的节点。

• 玩家走棋的层我们称为MIN层，这一层玩家要保证自己的利益最大化，那么就会选分最低的节点。

这也就是极大极小值搜索算法的名称由来。如上图，图中甲是电脑，乙是玩家，那么在甲层的时候，总是选其中值最大的节点，乙层的时候，总是选其中最小的节点。

而每一个节点的分数，都是由子节点决定的，因此我们对博弈树只能进行深度优先搜索而无法进行广度优先搜索。深度优先搜索用递归非常容易实现，然后主要工作其实是完成一个估值函数，这个函数需要对当前局势给出一个比较准确的评分。

实现极大值极小值搜索，就是是一个DFS，伪代码如下：

function minmax(board, depth)
	for move in board.getLegalMoves() do
        board.createMove( move );
        current = min( board );
        if current.getScore() > bestScoreSoFar then
        	bestScoreSoFar = current.getScore();
        	bestMove = current.getMove();
        board.resetMove( move );
   	return bestScoreSoFar;

function min( board, depth )
	if board.isTerminal() then
		return evaluate(board)
	else
		score = ∞
		for move in board.getLegalMoves() do
			board.createMove( move );
			result = max( board, depth-1 )
			board.resetMove( move );
			if (result < score)
            	score = result;
	return score;

function max( board, depth )
	if board.isTerminal() then
		return evaluate(board)
	else
		score = -∞
		for move in board.getLegalMoves() do
			board.createMove( move );
			result = min( board, depth-1 )
			board.resetMove( move );
			if (result > score)
            	score = result;
	return score;

但测试后发现该算法速度比较慢，对15×15的棋盘，搜索第一层有15×15=225个结点，第二层就约有15×15×15×15=50625个节点，完全是指数爆炸。

α-β剪枝算法

在搜索的过程中，实际上有搜索很多点是多余的。经过α-β剪枝，可以极大的减少搜索的数量。在查阅资料的过程中，发现α-β剪枝算法是一个基础而经典的算法，还有很多风格、很多变式，值得深入学习。

编译安装

create build director.

mkdir build
qmake ..
make